#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef char VertexType[4];
typedef char InfoPtr;
typedef int VRType;
#define INFINITY 100000 //定义一个无限大的值
#define MaxSize 50 //最大顶点个数
typedef int PathMatrix[MaxSize][MaxSize][MaxSize]; //定义一个保存最短路径的二维数组
typedef int ShortPathLength[MaxSize][MaxSize]; //定义一个保存从顶点v0到顶点v的最短距离的数组
typedef enum{DG,DN,UG,UN}GraphKind;
typedef struct{
VRType adj; //对于无权图,用1表示相邻,0表示不相邻;对于带权图,存储权值
InfoPtr *info; //与弧或边的相关信息
}ArcNode,AdjMatrix[MaxSize][MaxSize];
//图的类型定义
typedef struct{
VertexType vex[MaxSize]; //用于存储顶点
AdjMatrix arc; //邻接矩阵,存储边或弧的信息
int vexnum,arcnum; //顶点数和边(弧)的数目
GraphKind kind; //图的类型
}MGraph;
//加入一个存储网的行、列和权值的类型定义
typedef struct{
int row;
int col;
int weight;
}GNode;
//採用邻接矩阵表示法创建有向网N
void CreateGraph(MGraph *N,GNode *value,int vnum,int arcnum,VertexType *ch){
int i,j,k,w;
char s[MaxSize];
VertexType v1,v2;
N->vexnum=vnum;
N->arcnum=arcnum;
for(i=0;i<vnum;i++)
strcpy(N->vex[i],ch[i]);
//初始化邻接矩阵
for(i=0;i<N->vexnum;i++)
for(j=0;j<N->vexnum;j++){
N->arc[i][j].adj=INFINITY;
N->arc[i][j].info=NULL; //弧的信息初始化为空
}
for(k=0;k<arcnum;k++){
i=value[k].row;
j=value[k].col;
N->arc[i][j].adj=value[k].weight;
}
N->kind=DN; //图的类型为有向网
}
//输出邻接矩阵存储表示的图N
void DisplayGraph(MGraph N){
int i,j;
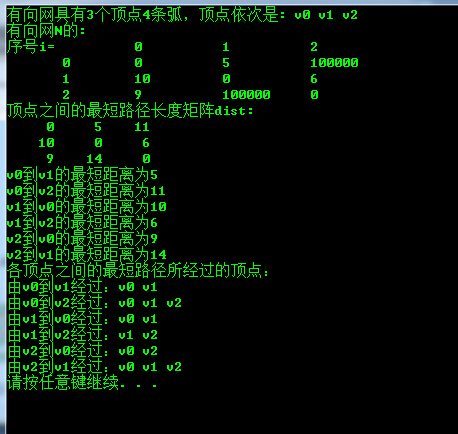
printf("有向网具有%d个顶点%d条弧,顶点依次是: ",N.vexnum,N.arcnum);
for(i=0;i<N.vexnum;++i) /*输出网的顶点*/
printf("%s ",N.vex[i]);
printf("\n有向网N的:\n"); /*输出网N的弧*/
printf("序号i=");
for(i=0;i<N.vexnum;i++)
printf("%11d",i);
printf("\n");
for(i=0;i<N.vexnum;i++)
{
printf(" %-6d ",i);
for(j=0;j<N.vexnum;j++)
printf("%-11d",N.arc[i][j].adj);
printf("\n");
}
}
//用Floyd算法求有向网N的各顶点v和w之间的最短路径,当中path[v][w][u]表示u是从v到w当前求得最短路径上的顶点
void Floyd(MGraph N,PathMatrix path,ShortPathLength dist){
int u,v,w,i;
for(v=0;v<N.vexnum;v++) //初始化数组path和dist
for(w=0;w<N.vexnum;w++){
dist[v][w]=N.arc[v][w].adj; //初始时。顶点v到顶点w的最短路径为v到w的弧的权值
for(u=0;u<N.vexnum;u++)
path[v][w][u]=0; //路径矩阵初始化为零
if(dist[v][w]<INFINITY){ //假设v到w有路径,则由v到w的路径经过v和w两点
path[v][w][v]=1;
path[v][w][w]=1;
}
}
for(u=0;u<N.vexnum;u++)
for(v=0;v<N.vexnum;v++)
for(w=0;w<N.vexnum;w++)
if(dist[v][u]<INFINITY&&dist[u][w]<INFINITY&&(dist[v][u]+dist[u][w]<dist[v][w])){ //从v经u到w的一条路径为当前最短的路径
dist[v][w]=dist[v][u]+dist[u][w]; //更新v到w的最短路径
for(i=0;i<N.vexnum;i++) //从v到w的路径经过从v到u和从u到w的全部路径
path[v][w][i]=path[v][u][i]||path[u][w][i];
}
}
void main(){
int w,u,v,vnum=3,arcnum=4;
MGraph N;
GNode value[]={{0,1,5},{1,0,10},{1,2,6},{2,0,9}};
VertexType ch[]={"v0","v1","v2"};
PathMatrix path; /*用二维数组存放最短路径所经过的顶点*/
ShortPathLength dist; /*用一维数组存放最短路径长度*/
CreateGraph(&N,value,vnum,arcnum,ch); /*创建有向网N*/
for(v=0;v<N.vexnum;v++)
N.arc[v][v].adj=0; /*弗洛伊德算法要求对角元素值为0。由于两点同样,其距离为0 */
DisplayGraph(N); /*输出有向网N*/
Floyd(N,path,dist);
printf("顶点之间的最短路径长度矩阵dist:\n");
for(u=0;u<N.vexnum;u++)
{
for(v=0;v<N.vexnum;v++)
printf("%6d",dist[u][v]);
printf("\n");
}
for(u=0;u<N.vexnum;u++)
for(v=0;v<N.vexnum;v++)
if(u!=v)
printf("%s到%s的最短距离为%d\n",N.vex[u],N.vex[v],dist[u][v]);
printf("各顶点之间的最短路径所经过的顶点:\n");
for(u=0;u<N.vexnum;u++)
for(v=0;v<N.vexnum;v++)
if(u!=v)
{
printf("由%s到%s经过:",N.vex[u],N.vex[v]);
for(w=0;w<N.vexnum;w++)
if(path[u][v][w]==1)
printf("%s ",N.vex[w]);
printf("\n");
}
system("pause");
}