【现代程序设计】【homework-03】【11061027】
Q:你现在使用的代码规范是什么, 和上课前有什么改进?
A: 代码规范........自定义的代码规范算 代码规范吗。。。。。
Q:你的同伴有哪些优点 (列出至少三点), 和那些需要改进的地方 (列出至少三点)
A:
Q:你的代码从 作业2 到 作业3 经历了哪些变化? 哪些代码需要重构 (看关于代码重构的资料), 哪些需要重写, 为什么?
A:因为作业2是用c写的,作业3用c#(wpf)写的,我打算做一个界面交互,而非命令行的maxsum,所以作业3的代码是基本上都是重写的
Q:你的设计是如何保证 不同的 maxsum.exe 命令行最后在一个GUI 的界面显示的?
A:由于做的是界面操作的应用,命令行显的不实用和麻烦,所以我没加入命令行这个功能,也就不存在【不同的 maxsum.exe 命令行最后在一个GUI 的界面显示的】的问题
|
Personal Software Process Stages |
时间百分比(%) |
实际花费的时间 (分钟) |
原来估计的时间 (分钟) |
|
|
计划 |
||||
|
· 估计这个任务需要多少时间,把工作细化并大致排序 |
0 | 0 | 0 | |
|
开发 |
||||
|
· 需求分析 (包括学习新技术) |
20 | 3h | 1h | |
|
· 生成设计文档 |
0 | 0 | 0 | |
|
· 设计复审 (和同事审核设计文档) |
0 | 0 | 0 | |
|
· 代码规范 (制定合适的规范) |
0 | 0 | 0 | |
|
· 具体设计 |
15 | 3h | 2h | |
|
· 具体编码 |
20 | 3h | 6h | |
|
· 代码复审 |
10 | 2h | 2h | |
|
· 测试(自我测试,修改代码,提交修改) |
35 | 7h | 4h | |
|
总结报告 |
||||
|
|
||||
| Total | 总计 | 100% | 总用时 18h | 总估计的用 15h |
总结:
因为对WPF不太熟悉,所以这次作业很多的时间花在了学习wpf上
一开始挑选显示二维数组的Xaml控件,google了半天,感觉好像是 DataGrid更方便一点。
然后就用datagrid显示二维数组
单独改变DataGrid的某个cell的背景色不会,Google了好一会
然后因为这个DataDrid的行列都是动态确定的,数据绑定又Google了好一会.....
在花了不少的时间搞定UI这一块之后 ,很快搞定了【子矩阵的问题】和【连通子图】
运行的时候发现,由于上次作业【连通子图】写的太懒,就一个递归,什么剪枝都没有 ,于是代码的时间效率实在是 渣
又重新写了一个【连通子图】的类,并重做了优化,这点又花了很长时间
虽然时间效率还是很渣,但是勉强还是解出来
最后就是烦人的测试,Debug...文件输入的Debug,AnyMaxsum的Debug,Maxsum的Debug,UI显示的Debug。。。
然后现在总算是完成了
下面是anymaxsum的c#代码
通过 GetResultData()获取 数据
1 namespace maxsum 2 { 3 class AnyMaxsum 4 { 5 bool[,] gTemp,gResult; 6 bool isvselect=false, ishselect=false; 7 int sumall=0,n,m,cpuload,amax; 8 public int sum=-10000, nsum = 0; 9 10 int[,] a, asum, gmain; 11 int[] dx={-1,0,1,0},dy={0,-1,0,1}; 12 13 14 void init() 15 { 16 for (int i = 0; i < m; i++) 17 for (int j = 0; j < n; j++) 18 { 19 gTemp[i, j] = gResult[i, j] = false; 20 gmain[i, j] = 0; 21 } 22 23 } 24 25 public AnyMaxsum(int Arrm,int Arrn,int[,] ArrSource) 26 { 27 n = Arrn; 28 m = Arrm; 29 a = new int[m, n]; 30 asum = new int[m, n]; 31 32 gTemp = new bool[m, n]; 33 gmain = new int[m, n]; 34 gResult = new bool[m, n]; 35 36 a = ArrSource; 37 for (int i = 0; i < m; i++) 38 for (int j = 0; j < m; j++) 39 { 40 if (a[i, j] > 0) sumall += a[i, j]; 41 asum[i, j] = sumall; 42 if (amax < a[i, j]) amax = a[i, j]; 43 } 44 45 } 46 47 public void setvh(bool v,bool h) 48 { 49 isvselect = v; 50 ishselect = h; 51 } 52 53 public void GetResultData(ref int s,ref bool[,] aresult) 54 { 55 init(); 56 if (sumall <= 0) 57 { 58 int x = 0, y = 0, z = -1234567891; 59 for (int i = 0; i < m; i++) 60 for (int j = 0; j < n; j++) if (z < a[i, j]) 61 { 62 z = a[i, j]; 63 x = i; 64 y = j; 65 } 66 s = z; 67 for (int i = 0; i < m; i++) 68 for (int j = 0; j < n; j++) aresult[i, j] = false; 69 aresult[x, y] = true; 70 return; 71 } 72 73 fany(0, -1, 0); 74 for (int i = 0; i < m; i++) 75 for (int j = 0; j < n; j++) aresult[i, j] = gResult[i, j]; 76 s = sum; 77 } 78 public int GetCpuLoad() 79 { 80 return cpuload; 81 } 82 83 bool isinvh(int x,int y) 84 { 85 if (x >= 0 && x < m && y >= 0 && y < n) 86 return true; 87 return false; 88 } 89 90 void ff(int x, int y) 91 { 92 int tx, ty, i; 93 94 gTemp[x, y] = true; 95 96 for (i = 0; i < 4; i++) 97 { 98 tx = x + dx[i]; 99 ty = y + dy[i]; 100 101 if (isvselect) 102 { 103 if (tx == m) tx = 0; 104 if (tx == -1) tx = m - 1; 105 } 106 107 if (ishselect) 108 { 109 if (ty == n) ty = 0; 110 if (ty == -1) ty = n - 1; 111 } 112 113 if (isinvh(tx, ty) && !gTemp[tx,ty] && gmain[tx,ty]<2) 114 ff(tx, ty); 115 } 116 } 117 118 void fany(int x, int y, int z) 119 { 120 int tx, ty, tt, i, j; 121 122 cpuload++; 123 124 for (i = 0; i <= x; i++) 125 for (j = 0; j < n; j++) 126 if (gmain[i, j] == 1) 127 { 128 tx = i; ty = j; 129 for (i = 0; i < m; i++) 130 for (j = 0; j < n; j++) gTemp[i, j] = false; 131 ff(tx, ty); 132 for (i = 0; i <= x; i++) 133 for (j = 0; j < n; j++) if (!gTemp[i, j] && gmain[i, j] == 1) return; 134 i = x + 1; 135 break; 136 } 137 138 139 if (x == m - 1 && y == n - 1) 140 { 141 142 143 if (sum > z) return; 144 145 tt = 0; 146 for (i = 0; i < m; i++) 147 for (j = 0; j < n; j++) if (gmain[i, j] == 1) 148 tt++; 149 150 if (sum == z && tt > nsum) return; 151 152 for (i = 0; i < m; i++) 153 for (j = 0; j < n; j++) if (gmain[i, j] == 1) 154 gResult[i, j] = true; 155 else gResult[i, j] = false; 156 157 sum = z; 158 nsum = tt; 159 return; 160 } 161 162 ty = (y + 1) % n; 163 tx = x + (y + 1) / n; 164 165 tt = sumall - asum[tx, ty] + z; 166 167 if (tt + a[tx, ty] >= sum) 168 { 169 gmain[tx, ty] = 1; 170 fany(tx, ty, z + a[tx, ty]); 171 gmain[tx, ty] = 0; 172 } 173 if (tt >= sum) 174 { 175 gmain[tx, ty] = 2; 176 fany(tx, ty, z); 177 gmain[tx, ty] = 0; 178 } 179 } 180 181 } 182 }
下面是工程文件和截图和测试数据:
测试数据:我一共写了14组测试数据,加上xinz老师的4组,18组测试数据
https://files.cnblogs.com/lightz/MaxsumTestData.zip
VS2012_工程文件:maxsum软件 包含在文件的bin\Release 目录下
https://files.cnblogs.com/lightz/Maxsum_VS2012.zip
截图:
https://files.cnblogs.com/lightz/Maxsum%E6%88%AA%E5%9B%BE.zip
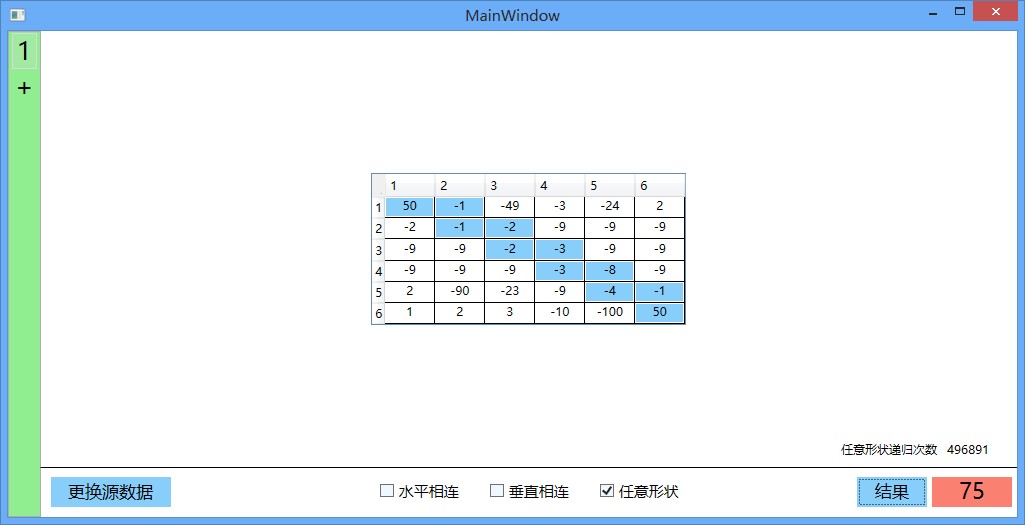
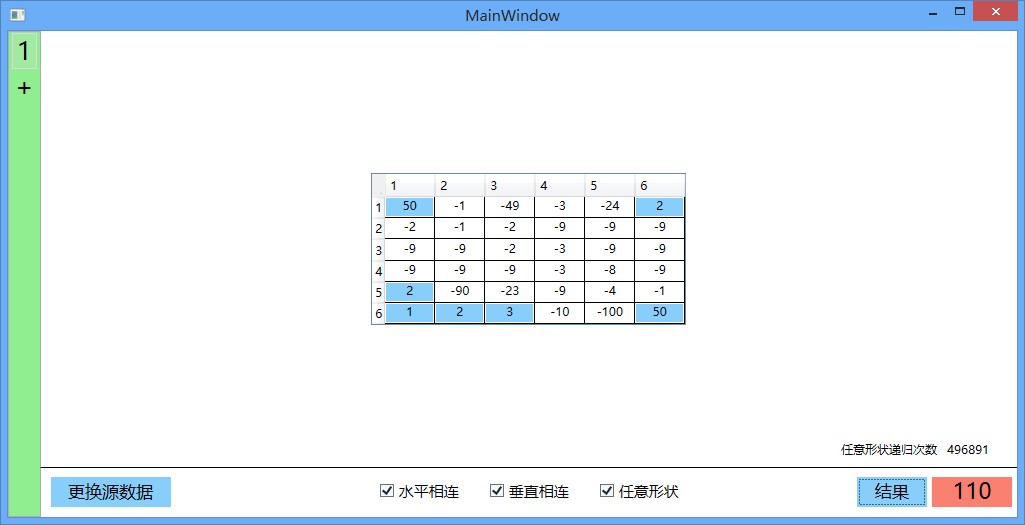
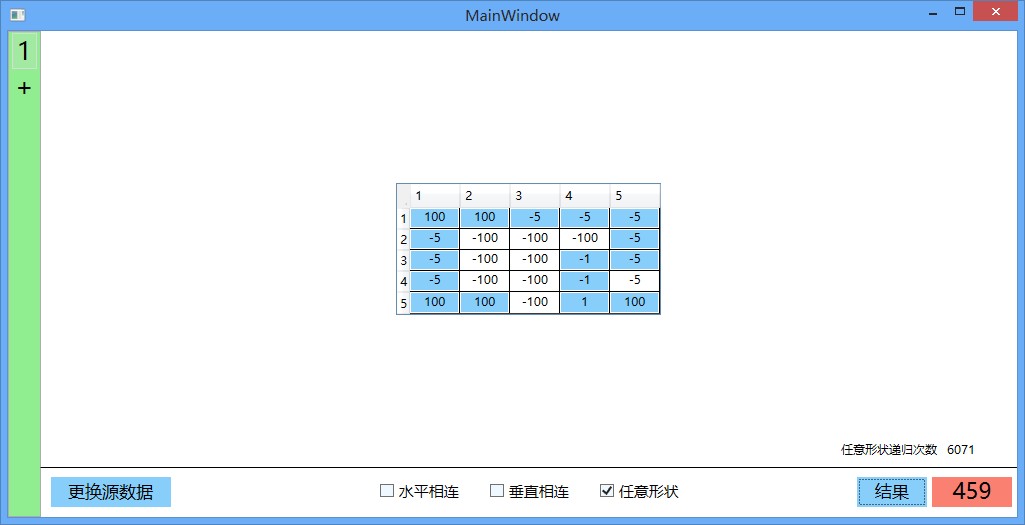
这里随便贴了几张,如下:







 浙公网安备 33010602011771号
浙公网安备 33010602011771号