数据结构（Python版）——3、基本结构
数据结构（Python版）——3、基本结构
什么是线性结构Linear Structure
线性结构是一种有序数据项的集合，其中每个数据项都有唯一的前驱和后继
除了第一个没有前驱，最后一个没有后继
新的数据项加入到数据集中是，只会加入到原有某个数据项之前或之后
具有这种性质的数据集，就称为线性结构
线性结构总有两端，在不同的情况下，两端的称呼也不同
有时候称为“左”“右”端、“前”“后”端、“顶”“底”端
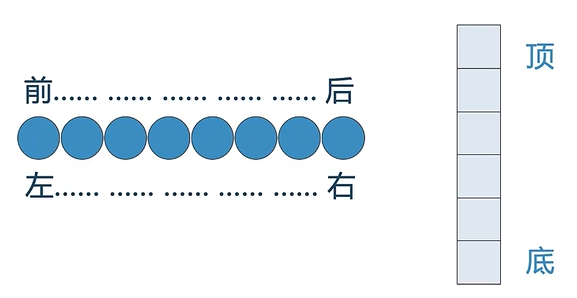
两端的称呼并不是关键，不同线性结构的关键区别在于数据项增减的方式
有的结构只允许数据项从一端添加，而有的结构则允许数据项从两端移除
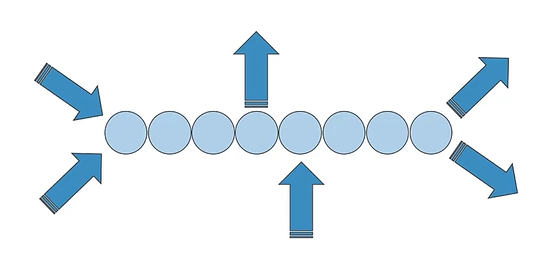
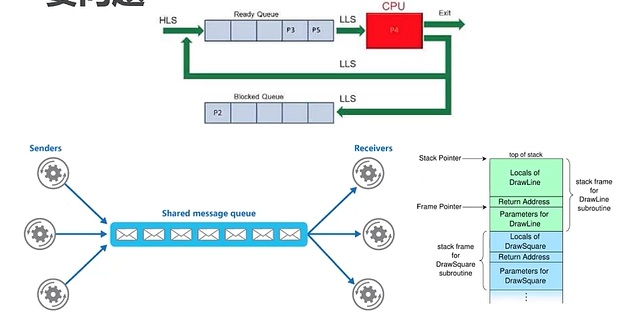
我们从4中最简单但功能强大的结构入手，开始研究数据结构
栈Stack，队列Queue，双端队列Deque和列表List
这些数据集的共同点在于，数据项之间只存在先后的次序，都是线性结构
这些线性结构是应用最广泛的数据结构，它们出现在各种算法中，用来解决大量重要问题
栈抽象数据类型及Python实现
栈Stack：什么是栈？
一种有次序的数据项集合，在栈中，数据项的加入和移除都仅发生在同一端
在这一端叫栈“顶top”，另一端叫栈“底base”
日常生活中有很多栈的应用
盘子、托盘、书堆等等
距离栈底越近的数据项，留在栈中的时间就越长
而最新加入栈的数据项会被最先移除
这种次序通常称为“后进先出LIFO”：Last in First out
这是一种基于数据项保存时间的次序，时间越短的离栈顶越近，而时间越长的离栈底越近
栈的特性：反转次序
我们观察一个由混合的Python原生数据对象形成的栈
进栈和出栈的次序正好相反
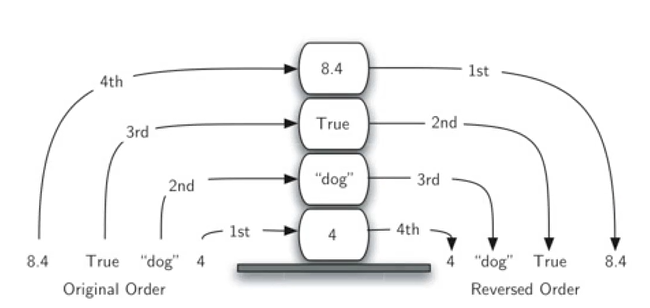
这种访问次序反转的特性，我们在某些计算机操作上碰到过
浏览器的“后退back”按钮，最先back的是最近访问的网页
world的“Undo”按钮，最先撤销的是最近操作
抽象数据类型Stack
抽象数据类型“栈”是一个有次序的数据集，每个数据项近从“栈顶”一端加入到数据集中、从数据集中移除，栈具有后进先出LIFO的特性
抽象数据类型“栈”定义为如下的操作
Stack():创建一个空栈，不包括任何数据项
push(item):将item加入栈顶，无返回值
pop():将栈顶数据项移除，并返回，栈被修改
peek():“窥视”栈顶数据项，返回栈顶的数据项但不移除，栈不被修改
isEmpty():返回栈是否为空栈
size():返回栈中有多少个数据项
抽象数据类型Stack：操作样例
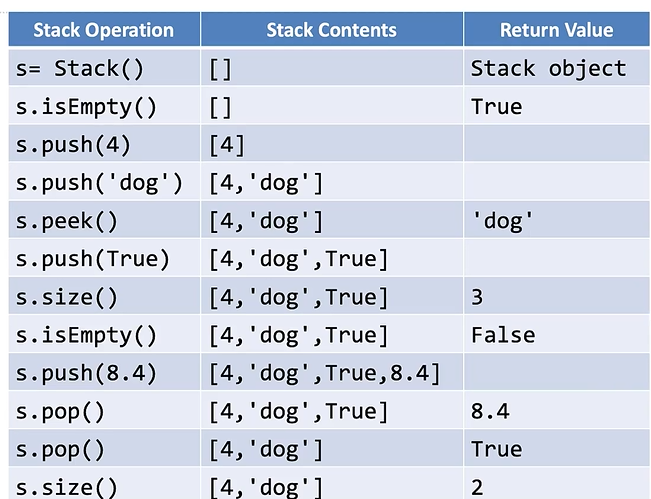
用Python实现ADT Stack
在清楚地定义了抽象数据类型Stack之后，我们看看如何用Python来实现它
Python的面向对象机制，可以用来实现用户自定义类型
将ADT Stack实现为Python的一个Class
将ADT Stack的操作实现为Class的方法
由于Stack是一个数据集，所以可以采用Python的原生数据集来实现，我们选用最常用的数据集List来实现
一个细节：Stack的两端对应list设置
可以将List的任意一端（index=0或者-1）设置为栈顶
我们选用List的末端（index=-1）作为栈顶
这样栈的操作就可以通过对list的append和pop来实现，很简单！
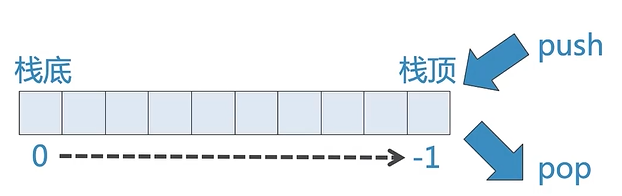
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
Stack测试代码
s = Stack()
print(s.isEmpty())
s.push(4)
s.push('dog')
print(s.peek())
s.push(True)
print(s.size())
print(s.isEmpty())
s.push(8.4)
print(s.pop())
print(s.pop())
print(s.size())
print(s.items)
实验结果：
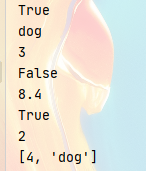
ADT Stack的另一个实现
如果我们把List的另一端（首端index=0）作为Stack的栈顶，同样也可以实现Stack
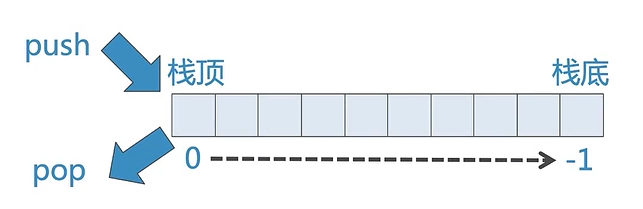
不同的实现方式保持了ADT接口的稳定性
但性能有所不同，栈顶首端的版本（左），其push/pop的复杂度为O(n)，而栈顶尾端的实现（右），其push/pop的复杂度为O(1)
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
# return self.items[len(self.items)-1]
return self.items[0]
def size(self):
return len(self.items)
未完待续
