逻辑推理——双方轮流拿球，拿到最后球者胜

转自： only_on_one

 

前天参加58集团笔试，最后的问答题有一道这样的题，事后推敲后觉得很有意思，就记录下来吧。
给定100个乒乓球，甲乙两人轮流拿，每人每次最少拿1个，最多拿6个，问有没有必胜的拿法，如有，哪方必胜？
答：有必胜的方法，先拿的必胜。通过列举法找到规律：

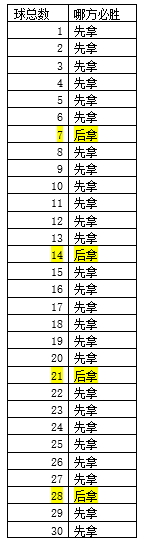
从上述规律可以看出，如果球总数为7的倍数，则后拿者按照一定的规律必胜；若球总数不为7的倍数，则先拿者按照一定的规律必胜。那这“一定的规律”是什么呢？就是，拿走一些球（当然拿走个数在1和6之间），使得剩下的球的总数为7的倍数。简单说就是：谁将剩下的球拿成7的倍数，谁就能赢。
其实，这里7还可以换成别的任何正整数，规律亦如此。