POJ 2632:Crashing Robots
Crashing Robots
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 8424 | Accepted: 3648 |
Description
In a modernized warehouse, robots are used to fetch the goods. Careful planning is needed to ensure that the robots reach their destinations without crashing into each other. Of course, all warehouses are rectangular, and all robots occupy a circular floor
space with a diameter of 1 meter. Assume there are N robots, numbered from 1 through N. You will get to know the position and orientation of each robot, and all the instructions, which are carefully (and mindlessly) followed by the robots. Instructions are
processed in the order they come. No two robots move simultaneously; a robot always completes its move before the next one starts moving.
A robot crashes with a wall if it attempts to move outside the area of the warehouse, and two robots crash with each other if they ever try to occupy the same spot.
A robot crashes with a wall if it attempts to move outside the area of the warehouse, and two robots crash with each other if they ever try to occupy the same spot.
Input
The first line of input is K, the number of test cases. Each test case starts with one line consisting of two integers, 1 <= A, B <= 100, giving the size of the warehouse in meters. A is the length in the EW-direction, and B in the NS-direction.
The second line contains two integers, 1 <= N, M <= 100, denoting the numbers of robots and instructions respectively.
Then follow N lines with two integers, 1 <= Xi <= A, 1 <= Yi <= B and one letter (N, S, E or W), giving the starting position and direction of each robot, in order from 1 through N. No two robots start at the same position.
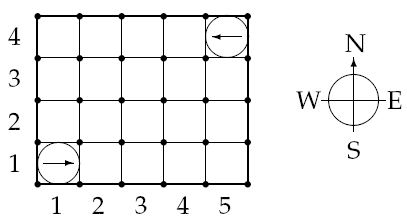
Figure 1: The starting positions of the robots in the sample warehouse
Finally there are M lines, giving the instructions in sequential order.
An instruction has the following format:
< robot #> < action> < repeat>
Where is one of
and 1 <= < repeat> <= 100 is the number of times the robot should perform this single move.
The second line contains two integers, 1 <= N, M <= 100, denoting the numbers of robots and instructions respectively.
Then follow N lines with two integers, 1 <= Xi <= A, 1 <= Yi <= B and one letter (N, S, E or W), giving the starting position and direction of each robot, in order from 1 through N. No two robots start at the same position.

Figure 1: The starting positions of the robots in the sample warehouse
Finally there are M lines, giving the instructions in sequential order.
An instruction has the following format:
< robot #> < action> < repeat>
Where is one of
- L: turn left 90 degrees,
- R: turn right 90 degrees, or
- F: move forward one meter,
and 1 <= < repeat> <= 100 is the number of times the robot should perform this single move.
Output
Output one line for each test case:
Only the first crash is to be reported.
- Robot i crashes into the wall, if robot i crashes into a wall. (A robot crashes into a wall if Xi = 0, Xi = A + 1, Yi = 0 or Yi = B + 1.)
- Robot i crashes into robot j, if robots i and j crash, and i is the moving robot.
- OK, if no crashing occurs.
Only the first crash is to be reported.
Sample Input
4 5 4 2 2 1 1 E 5 4 W 1 F 7 2 F 7 5 4 2 4 1 1 E 5 4 W 1 F 3 2 F 1 1 L 1 1 F 3 5 4 2 2 1 1 E 5 4 W 1 L 96 1 F 2 5 4 2 3 1 1 E 5 4 W 1 F 4 1 L 1 1 F 20
Sample Output
Robot 1 crashes into the wall Robot 1 crashes into robot 2 OK Robot 1 crashes into robot 2
题意是给定一个坐标地图,给了很多个机器人的坐标和方向,有三种对机器人的操作方式,F是前进,L是向左转,R向右转。看哪一个机器人先撞墙或是撞到其他机器人。
自己需要注意两点:
1.不一定非得到操作机器人的时候才有冲突,可能在最开始的机器人拜访过程中机器人站的位置就已经重复,即冲突了。
2.R向右转,自己定义成为-1,原来自己以为负数除以数的余数会是正数,结果自己too naive了,要考虑将其变为正数。
这个题自己就注意这两点就够了,因为本身就是一个模拟的过程,跟算法也没什么关系。。。
代码:
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#pragma warning(disable:4996)
using namespace std;
struct R
{
int x;
int y;
int dir;
}Robot[110];
enum{ E,N,W,S };
enum{ L=1,R=-1};
int map_f[200][200];
int move_x[5]={1,0,-1,0};
int move_y[5]={0,1,0,-1};
int Test,X,Y,Robot_n,Q,i,flag;
string temp;
void solve()
{
int cal_n,cishu,k;
string manu;
cin>>cal_n>>manu>>cishu;
if(flag==0)
return;
if(manu=="F")
{
map_f[Robot[cal_n].x][Robot[cal_n].y]=0;
for(k=1;k<=cishu;k++)
{
Robot[cal_n].x = Robot[cal_n].x + move_x[Robot[cal_n].dir];
Robot[cal_n].y = Robot[cal_n].y + move_y[Robot[cal_n].dir];
if(Robot[cal_n].x <=0 || Robot[cal_n].y <=0 || Robot[cal_n].x >X || Robot[cal_n].y >Y)
{
flag=0;
cout<<"Robot "<<cal_n<<" crashes into the wall"<<endl;
break;
}
else if(map_f[Robot[cal_n].x][Robot[cal_n].y])
{
flag=0;
cout<<"Robot "<<cal_n<<" crashes into robot "<<map_f[Robot[cal_n].x][Robot[cal_n].y]<<endl;
break;
}
}
map_f[Robot[cal_n].x][Robot[cal_n].y]=cal_n;
}
else if(manu=="L")
{
Robot[cal_n].dir = (Robot[cal_n].dir + L*cishu)%4;
}
else if(manu=="R")
{
Robot[cal_n].dir = (Robot[cal_n].dir + (R*cishu)%4 + 4)%4;
}
}
int main()
{
cin>>Test;
while(Test--)
{
flag=1;
memset(map_f,0,sizeof(map_f));
cin>>X>>Y;
cin>>Robot_n>>Q;
for(i=1;i<=Robot_n;i++)
{
cin>>Robot[i].x>>Robot[i].y;
if(map_f[Robot[i].x][Robot[i].y])
{
flag=0;
cout<<"Robot "<<i<<" crashes into robot "<<map_f[Robot[i].x][Robot[i].y]<<endl;
}
else
{
map_f[Robot[i].x][Robot[i].y]=i;
}
cin>>temp;
if(temp=="E")
Robot[i].dir=E;
else if(temp=="N")
Robot[i].dir=N;
else if(temp=="W")
Robot[i].dir=W;
else if(temp=="S")
Robot[i].dir=S;
}
for(i=1;i<=Q;i++)
{
solve();
}
if(flag)
cout<<"OK"<<endl;
}
//system("pause");
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。




