POJ 3009:Curling 2.0 推箱子
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 14090 | Accepted: 5887 |
Description
On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.
Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
- At the beginning, the stone stands still at the start square.
- The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
- When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
- Once thrown, the stone keeps moving to the same direction until one of the following occurs:
- The stone hits a block (Fig. 2(b), (c)).
- The stone stops at the square next to the block it hit.
- The block disappears.
- The stone gets out of the board.
- The game ends in failure.
- The stone reaches the goal square.
- The stone stops there and the game ends in success.
- The stone hits a block (Fig. 2(b), (c)).
- You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.
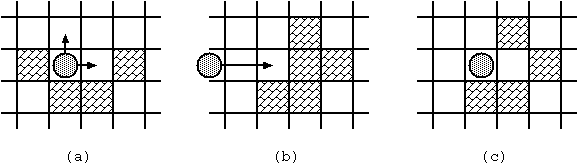
Fig. 2: Stone movements
Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).
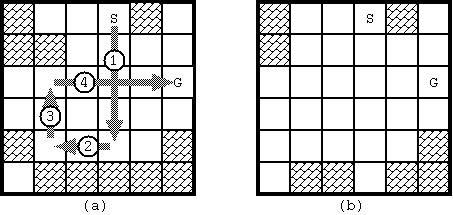
Fig. 3: The solution for Fig. D-1 and the final board configuration
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.
Each dataset is formatted as follows.
the width(=w) and the height(=h) of the board
First row of the board
...
h-th row of the board
The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.
Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.
0 vacant square 1 block 2 start position 3 goal position
The dataset for Fig. D-1 is as follows:
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
Output
For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.
Sample Input
2 1 3 2 6 6 1 0 0 2 1 0 1 1 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 6 1 1 1 2 1 1 3 6 1 1 0 2 1 1 3 12 1 2 0 1 1 1 1 1 1 1 1 1 3 13 1 2 0 1 1 1 1 1 1 1 1 1 1 3 0 0
Sample Output
1 4 -1 4 10 -1
冰球,我更喜欢把它叫推箱子,题意就是它这个箱子可以上下左右四个方向推,碰到边界就跑出去,碰到障碍物停止,之后碰到的障碍物就会在地图上消失,问从S开始经过几步可以达到E,超过10步的话就输出-1。
深搜,自己认为还是比较简单,毕竟模拟一遍,也不需要弄什么算法。
代码:
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#pragma warning(disable:4996)
using namespace std;
#define up 0
#define down 1
#define left 2
#define right 3
int value[25][25];
int row,col,flag,tui_x,tui_y,result,result_zuizhong;
bool can_tui(int x_r,int y_r,int dir)
{
if(dir==up||dir==down)
{
int i,j;
if(dir==up)
{
if(value[x_r-1][y_r]==1)
return false;
for(i=1;i<x_r;i++)
{
if(value[i][y_r])
return true;
}
return false;
}
else
{
if(value[x_r+1][y_r]==1)
return false;
for(i=x_r+1;i<=row;i++)
{
if(value[i][y_r])
return true;
}
return false;
}
}
else
{
int i,j;
if(dir==left)
{
if(value[x_r][y_r-1]==1)
return false;
for(i=1;i<y_r;i++)
{
if(value[x_r][i])
return true;
}
return false;
}
else
{
if(value[x_r][y_r+1]==1)
return false;
for(i=y_r+1;i<=col;i++)
{
if(value[x_r][i])
return true;
}
return false;
}
}
}
void tui(int x_r,int y_r,int dir)
{
int i,j;
if(dir==up)
{
for(i=x_r-1;i>=1;i--)
{
if(value[i][y_r]==1)
{
tui_x=i+1;
tui_y=y_r;
return;
}
if(value[i][y_r]==3)
{
tui_x=i;
tui_y=y_r;
return;
}
}
}
else if(dir==down)
{
for(i=x_r+1;i<=row;i++)
{
if(value[i][y_r]==1)
{
tui_x=i-1;
tui_y=y_r;
return;
}
if(value[i][y_r]==3)
{
tui_x=i;
tui_y=y_r;
return;
}
}
}
else if(dir==left)
{
for(i=y_r-1;i>=1;i--)
{
if(value[x_r][i]==1)
{
tui_x=x_r;
tui_y=i+1;
return;
}
if(value[x_r][i]==3)
{
tui_x=x_r;
tui_y=i;
return;
}
}
}
else
{
for(i=y_r+1;i<=col;i++)
{
if(value[x_r][i]==1)
{
tui_x=x_r;
tui_y=i-1;
return;
}
if(value[x_r][i]==3)
{
tui_x=x_r;
tui_y=i;
return;
}
}
}
}
void dfs(int x_r,int y_r,int step,int dir)
{
if(step>11)
return;
if(value[x_r][y_r]==3)
{
flag=1;
result=min(result,step);
return;
}
if(dir==up)
{
value[x_r-1][y_r]=0;
}
else if(dir==down)
{
value[x_r+1][y_r]=0;
}
else if(dir==left)
{
value[x_r][y_r-1]=0;
}
else if(dir==right)
{
value[x_r][y_r+1]=0;
}
if(can_tui(x_r,y_r,up))
{
tui(x_r,y_r,up);
int temp_x=tui_x;
int temp_y=tui_y;
dfs(temp_x,temp_y,step+1,up);
}
if(can_tui(x_r,y_r,left))
{
tui(x_r,y_r,left);
int temp_x=tui_x;
int temp_y=tui_y;
dfs(temp_x,temp_y,step+1,left);
}
if(can_tui(x_r,y_r,down))
{
tui(x_r,y_r,down);
int temp_x=tui_x;
int temp_y=tui_y;
dfs(temp_x,temp_y,step+1,down);
}
if(can_tui(x_r,y_r,right))
{
tui(x_r,y_r,right);
int temp_x=tui_x;
int temp_y=tui_y;
dfs(temp_x,temp_y,step+1,right);
}
if(dir==up)
{
value[x_r-1][y_r]=1;
}
else if(dir==down)
{
value[x_r+1][y_r]=1;
}
else if(dir==left)
{
value[x_r][y_r-1]=1;
}
else if(dir==right)
{
value[x_r][y_r+1]=1;
}
}
void solve()
{
int i,j;
for(i=row;i>=1;i--)
{
for(j=col;j>=1;j--)
{
if(value[i][j]==2)
{
value[i][j]=0;
result=11;
dfs(i,j,0,-1);
if(flag)
{
result_zuizhong =min(result,result_zuizhong);
}
return;
}
}
}
}
int main()
{
int i,j;
while(cin>>col>>row)
{
if(col+row==0)
break;
flag=0;
result_zuizhong=11;
memset(value,0,sizeof(value));
for(i=1;i<=row;i++)
{
for(j=1;j<=col;j++)
{
cin>>value[i][j];
}
}
solve();
if(result_zuizhong==11)
cout<<-1<<endl;
else
cout<<result_zuizhong<<endl;
}
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。




