POJ 1080：Human Gene Functions LCS经典DP

Human Gene Functions

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 18007		Accepted: 10012

Description

It is well known that a human gene can be considered as a sequence, consisting of four nucleotides, which are simply denoted by four letters, A, C, G, and T. Biologists have been interested in identifying human genes and determining their functions, because these can be used to diagnose human diseases and to design new drugs for them. 

A human gene can be identified through a series of time-consuming biological experiments, often with the help of computer programs. Once a sequence of a gene is obtained, the next job is to determine its function. 
One of the methods for biologists to use in determining the function of a new gene sequence that they have just identified is to search a database with the new gene as a query. The database to be searched stores many gene sequences and their functions – many researchers have been submitting their genes and functions to the database and the database is freely accessible through the Internet. 

A database search will return a list of gene sequences from the database that are similar to the query gene. 
Biologists assume that sequence similarity often implies functional similarity. So, the function of the new gene might be one of the functions that the genes from the list have. To exactly determine which one is the right one another series of biological experiments will be needed. 

Your job is to make a program that compares two genes and determines their similarity as explained below. Your program may be used as a part of the database search if you can provide an efficient one. 
Given two genes AGTGATG and GTTAG, how similar are they? One of the methods to measure the similarity 
of two genes is called alignment. In an alignment, spaces are inserted, if necessary, in appropriate positions of 
the genes to make them equally long and score the resulting genes according to a scoring matrix. 

For example, one space is inserted into AGTGATG to result in AGTGAT-G, and three spaces are inserted into GTTAG to result in –GT--TAG. A space is denoted by a minus sign (-). The two genes are now of equal 
length. These two strings are aligned: 

AGTGAT-G 
-GT--TAG 

In this alignment, there are four matches, namely, G in the second position, T in the third, T in the sixth, and G in the eighth. Each pair of aligned characters is assigned a score according to the following scoring matrix. 

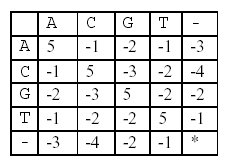
denotes that a space-space match is not allowed. The score of the alignment above is (-3)+5+5+(-2)+(-3)+5+(-3)+5=9. 

Of course, many other alignments are possible. One is shown below (a different number of spaces are inserted into different positions): 

AGTGATG 
-GTTA-G 

This alignment gives a score of (-3)+5+5+(-2)+5+(-1) +5=14. So, this one is better than the previous one. As a matter of fact, this one is optimal since no other alignment can have a higher score. So, it is said that the 
similarity of the two genes is 14.

Input

The input consists of T test cases. The number of test cases ) (T is given in the first line of the input file. Each test case consists of two lines: each line contains an integer, the length of a gene, followed by a gene sequence. The length of each gene sequence is at least one and does not exceed 100.

Output

The output should print the similarity of each test case, one per line.

Sample Input

2 
7 AGTGATG 
5 GTTAG 
7 AGCTATT 
9 AGCTTTAAA 

Sample Output

14
21

题意是要找一对基因序列的最大相似度。这个最大相似度来源于每一对字母的相似度相加(方框里的)，但让人蛋疼的是，每一对字母之间是可以错位的，不一定是一对一那么匹配，可以空出来一位让‘-’去和原字母匹配去，所以这样就增加了难度，要用DP。

这个题我真的是想递推关系想不出来啊啊啊，结果看了discuss中的思路才明白过来，是这样：

假设上面序列的是A1A2A3A4......Am

下面序列式B1B2B3B4....Bn，然后用f[m][n]表示A长度为m，B长度为n时的最大相似程度。

好，我们假设现在比对的是Am和Bn这里，比对这里的话，就有三个情况：

1)Am=Bn

这样结果会是:

XXXXXAm

XXXXXBn

那么此时递推的关系也就是

f[m][n]=f[m-1][n-1]+pipei(Am,Bn)

2)Am不等于Bn

这样结果可能会是

XXXXXAm

XXXXX  -

那么此时的递推关系就是

f[m][n]=f[m-1][n]+pipei(Am,'-')

3)Am不等于Bn

XXXXX  -

XXXXX Bn

此时的递推关系是f[m][n-1]+pipei('-',Bn)，从这三个情况中选择最大值。

递推关系是这样的话，是必须初始化的(因为存在着最佳匹配是第一个字符与‘-’匹配的情况)

即f[m][0]=f[m-1][0]+pipei(Am,'-')

    f[0][n]=f[0][n-1]+pipei('-',Bn)

代码：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#include <map>
#pragma warning(disable:4996)
using namespace std;

int matrix[5][5]={{5,-1,-2,-1,-3},
	              {-1,5,-3,-2,-4},
                  {-2,-3,5,-2,-2},
                  {-1,-2,-2,5,-1},
                  {-3,-4,-2,-1,0}
};
map<char,int>pair1;
int num1,num2;
char test1[150],test2[150];
int dp[150][150];

void cal()
{
	memset(dp,0,sizeof(dp));

	int i,j;
	for(i=0;i<num1;i++)
	{
		dp[i+1][0]=dp[i][0]+matrix[pair1[test1[i]]][pair1['-']];
	}
	for(j=0;j<num2;j++)
	{
		dp[0][j+1]=dp[0][j]+matrix[pair1['-']][pair1[test2[j]]];
	}
	for(i=0;i<num1;i++)
	{
		for(j=0;j<num2;j++)
		{
			dp[i+1][j+1]= max(dp[i][j]+matrix[pair1[test1[i]]][pair1[test2[j]]],
				              max(dp[i][j+1]+matrix[pair1[test1[i]]][pair1['-']],dp[i+1][j]+matrix[pair1['-']][pair1[test2[j]]]));
		}
	}
	cout<<dp[num1][num2]<<endl;
}

int main()
{	
	pair1['A']=0;
	pair1['C']=1;
	pair1['G']=2;
	pair1['T']=3;
	pair1['-']=4;

	int Test;
	scanf("%d",&Test);

	while(Test--)
	{
		cin>>num1>>test1;
		cin>>num2>>test2;
		
		cal();
	}
	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。