A Knight’s Tour --- BackTracking

A Knight’s Tour

https://www.tutorialspoint.com/The-Knight-s-tour-problem

In chess, we know that the knight can jump in a special manner. It can move either two squares horizontally and one square vertically or two squares vertically and one square horizontally in each direction, So the complete movement looks like English letter ‘L’.

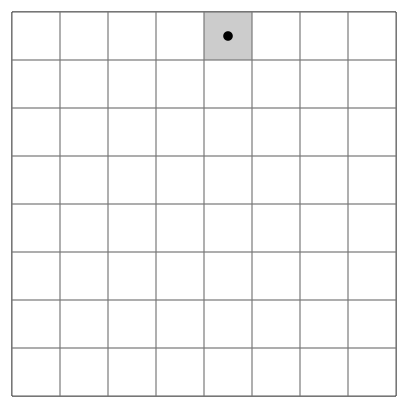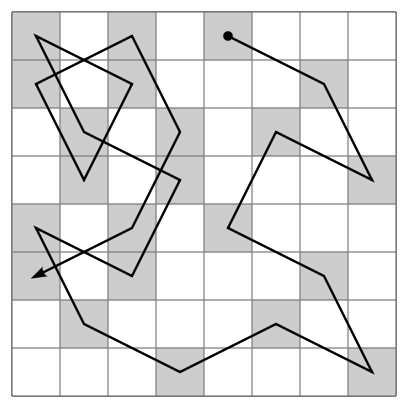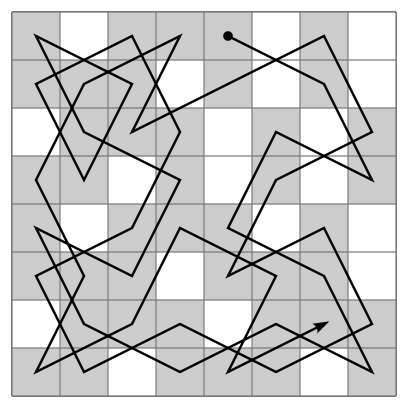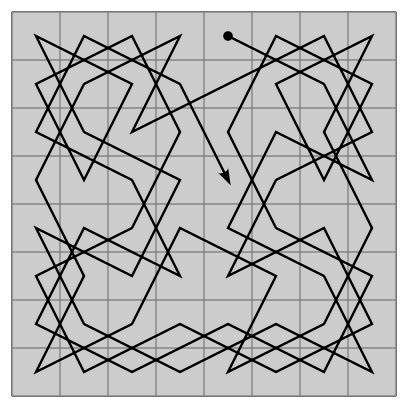
In this problem, there is an empty chess board, and a knight starting from any location in the board, our task is to check whether the knight can visit all of the squares in the board or not. When It can visit all of the squares, then place the number of jumps needed to reach that location from the starting point.

This problem can have multiple solutions, but we will try to find one possible solution.

Input and Output

Input:  
The size of a chess board. Generally, it is 8. as (8 x 8 is the size of a normal chess board.)
Output:
The knight’s moves. Each cell holds a number, that indicates where to start and the knight will reach a cell at which move.

  0  59  38  33  30  17   8  63
 37  34  31  60   9  62  29  16
 58   1  36  39  32  27  18   7
 35  48  41  26  61  10  15  28
 42  57   2  49  40  23   6  19
 47  50  45  54  25  20  11  14
 56  43  52   3  22  13  24   5
 51  46  55  44  53   4  21  12

 

https://bradfieldcs.com/algos/graphs/knights-tour/

The knight’s tour puzzle is played on a chess board with a single chess piece, the knight. The object of the puzzle is to find a sequence of moves that allow the knight to visit every square on the board exactly once, like so:

 

 

Solution

https://www.geeksforgeeks.org/the-knights-tour-problem-backtracking-1/

Backtracking works in an incremental way to attack problems. Typically, we start from an empty solution vector and one by one add items (Meaning of item varies from problem to problem. In the context of Knight’s tour problem, an item is a Knight’s move). When we add an item, we check if adding the current item violates the problem constraint, if it does then we remove the item and try other alternatives. If none of the alternatives works out then we go to the previous stage and remove the item added in the previous stage. If we reach the initial stage back then we say that no solution exists. If adding an item doesn’t violate constraints then we recursively add items one by one. If the solution vector becomes complete then we print the solution.

Backtracking Algorithm for Knight’s tour 

Following is the Backtracking algorithm for Knight’s tour problem. 

If all squares are visited 
    print the solution
Else
   a) Add one of the next moves to solution vector and recursively 
   check if this move leads to a solution. (A Knight can make maximum 
   eight moves. We choose one of the 8 moves in this step).
   b) If the move chosen in the above step doesn't lead to a solution
   then remove this move from the solution vector and try other 
   alternative moves.
   c) If none of the alternatives work then return false (Returning false 
   will remove the previously added item in recursion and if false is 
   returned by the initial call of recursion then "no solution exists" )

Time Complexity : 
There are N² Cells and for each, we have a maximum of 8 possible moves to choose from, so the worst running time is O(8^{N^2}).

Auxiliary Space: O(N²)

 

Code

https://www.tutorialspoint.com/The-Knight-s-tour-problem

#include <iostream>
#include <iomanip>
#define N 8

using namespace std;
int sol[N][N];

bool isValid(int x, int y, int sol[N][N]) {     //check place is in range and not assigned yet
   return ( x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1);
}

void displaySolution() {
   for (int x = 0; x < N; x++) {
      for (int y = 0; y < N; y++)
         cout << setw(3) << sol[x][y] << " ";
      cout << endl;
   }
}

int knightTour(int x, int y, int move, int sol[N][N], int xMove[N], int yMove[N]) {
   int xNext, yNext;
   if (move == N*N)     //when the total board is covered
      return true;

   for (int k = 0; k < 8; k++) {
      xNext = x + xMove[k];
      yNext = y + yMove[k];
      if (isValid(xNext, yNext, sol)) {     //check room is preoccupied or not
         sol[xNext][yNext] = move;
         if (knightTour(xNext, yNext, move+1, sol, xMove, yMove) == true)
            return true;
         else
            sol[xNext][yNext] = -1;// backtracking
      }
   }
   return false;
}

bool findKnightTourSol() {
   for (int x = 0; x < N; x++)     //initially set all values to -1 of solution matrix
      for (int y = 0; y < N; y++)
         sol[x][y] = -1;
   //all possible moves for knight
   int xMove[8] = {  2, 1, -1, -2, -2, -1,  1,  2 };
   int yMove[8] = {  1, 2,  2,  1, -1, -2, -2, -1 };
   sol[0][0]  = 0;     //starting from room (0, 0)

   if (knightTour(0, 0, 1, sol, xMove, yMove) == false) {
      cout << "Solution does not exist";
      return false;
   } else
      displaySolution();
   return true;
}

int main() {
   findKnightTourSol();
}

 

 

类似回溯方法可解的问题

N QUEEN PROBLEM

https://www.tutorialspoint.com/N-Queen-Problem

https://www.geeksforgeeks.org/n-queen-problem-backtracking-3/?ref=lbp

 

RAT IN MAZE

https://www.geeksforgeeks.org/rat-in-a-maze-backtracking-2/?ref=lbp