Search Algorithms in AI

Search Algorithms in AI

https://www.geeksforgeeks.org/search-algorithms-in-ai/?ref=lbp

搜索算法是agent在特定背景下执行目标搜索的方法。

搜索问题包括：

• 状态空间
• 启始状态
• 目标状态
• 目标检测函数

解决方法，对应一系列动作，或者叫做规划，一步一步从开始状态移动到目标状态。

 

Artificial Intelligence is the study of building agents that act rationally. Most of the time, these agents perform some kind of search algorithm in the background in order to achieve their tasks.

• A search problem consists of: 
  • A State Space. Set of all possible states where you can be.
  • A Start State. The state from where the search begins.
  • A Goal Test. A function that looks at the current state returns whether or not it is the goal state.
• The Solution to a search problem is a sequence of actions, called the plan that transforms the start state to the goal state.
• This plan is achieved through search algorithms.

 

Types of search algorithms:

搜索算法分为两个类型：

• 无告知搜索
• 有告知搜索

 https://www.geeksforgeeks.org/difference-between-informed-and-uninformed-search-in-ai/?ref=rp

 

There are far too many powerful search algorithms out there to fit in a single article. Instead, this article will discuss six of the fundamental search algorithms, divided into two categories, as shown below. 

 

Note that there is much more to search algorithms than the chart I have provided above. However, this article will mostly stick to the above chart, exploring the algorithms given there.

 

Difference of Informed and Uninformed

https://www.cs.cmu.edu/~motionplanning/lecture/AppH-astar-dstar_howie.pdf

 

 

 

 

 

 

 

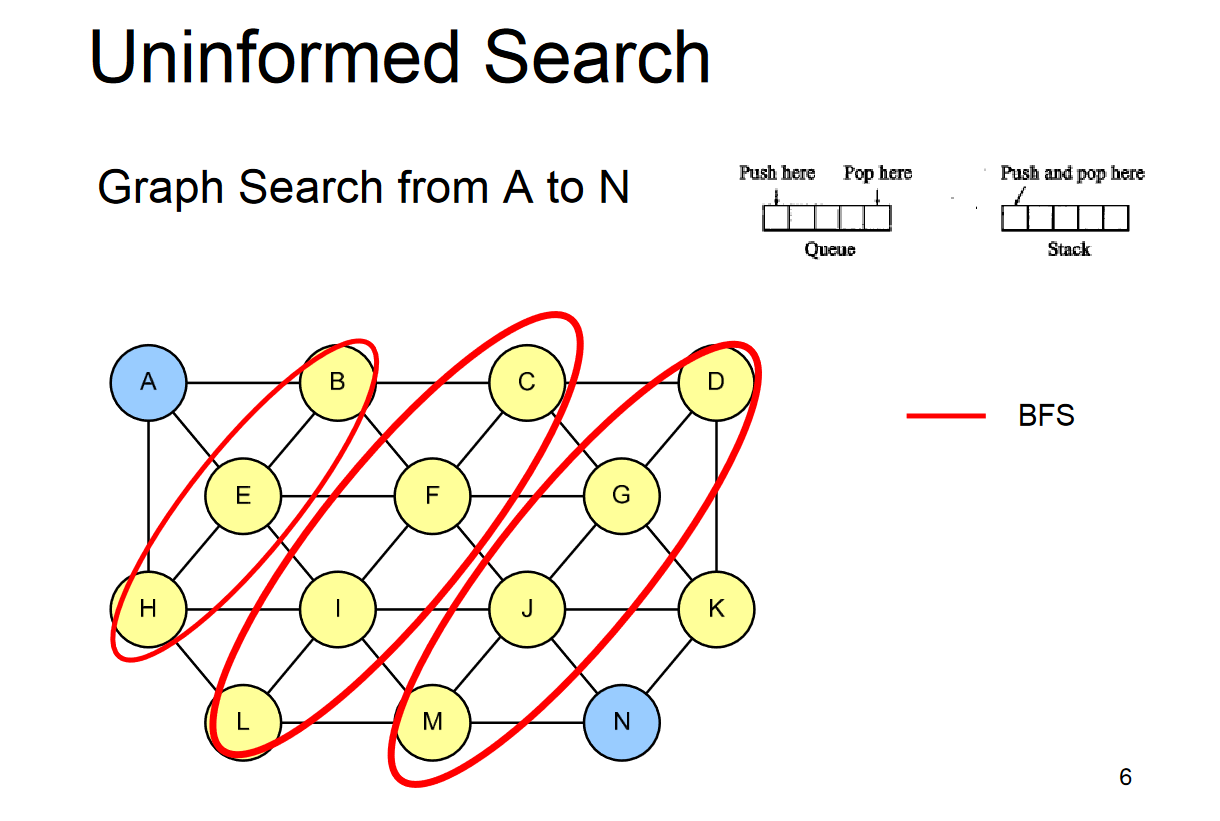
Uninformed Search Algorithms:

无告知搜索，

对应没有任何额外的信息关于目标状态的， 除了问题的定义。

可以理解为， 别人让你去找一个人，仅仅告诉你这个人的名字， 不告诉你他大概在什么位置。

 

The search algorithms in this section have no additional information on the goal node other than the one provided in the problem definition. The plans to reach the goal state from the start state differ only by the order and/or length of actions. Uninformed search is also called Blind search. These algorithms can only generate the successors and differentiate between the goal state and non goal state. 

The following uninformed search algorithms are discussed in this section.

1. Depth First Search
2. Breadth First Search
3. Uniform Cost Search

Each of these algorithms will have: 

• A problem graph, containing the start node S and the goal node G.
• A strategy, describing the manner in which the graph will be traversed to get to G.
• A fringe, which is a data structure used to store all the possible states (nodes) that you can go from the current states.
• A tree, that results while traversing to the goal node.
• A solution plan, which the sequence of nodes from S to G.

 

Depth First Search:

对所有节点进行遍历的方法， 以深度方向优先。

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. It uses last in- first-out strategy and hence it is implemented using a stack.

 

Breadth First Search:

对所有节点进行遍历的方法， 以广度方向优先。

Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key’), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level. It is implemented using a queue.

 

Uniform Cost Search:

统一花费搜索， 是dijkstra的变种， 在所搜的过程中， 考虑到了待搜目标的花费，寻找最小花费的解决方案。

UCS is different from BFS and DFS because here the costs come into play. In other words, traversing via different edges might not have the same cost. The goal is to find a path where the cumulative sum of costs is the least. 

Cost of a node is defined as: 

  cost(node) = cumulative cost of all nodes from root
  cost(root) = 0

 

Informed Search Algorithms:

有告知搜索算法

此算法利用目标节点的信息， 这些信息可以帮助更加高效搜索。

这些信息通过一些启发式方法获得。

启发式方法--式对当前状态到目标状态的距离估计

Here, the algorithms have information on the goal state, which helps in more efficient searching. This information is obtained by something called a heuristic. 
In this section, we will discuss the following search algorithms. 

1. Greedy Search
2. A* Tree Search
3. A* Graph Search

Search Heuristics: In an informed search, a heuristic is a function that estimates how close a state is to the goal state. For example – Manhattan distance, Euclidean distance, etc. (Lesser the distance, closer the goal.) Different heuristics are used in different informed algorithms discussed below.

 

Greedy Search:

贪婪算法， 扩展距离目标状态最近的节点， 这里的最近式估算值。

In greedy search, we expand the node closest to the goal node. The “closeness” is estimated by a heuristic h(x). 

Heuristic: A heuristic h is defined as- 
h(x) = Estimate of distance of node x from the goal node. 
Lower the value of h(x), closer is the node from the goal. 

Strategy: Expand the node closest to the goal state, i.e. expand the node with a lower h value.

 

A* Tree Search:

A星树的搜索算法，结合了 Uniform-cost搜索（dijstra算法变种）和 贪婪算法的 优点。

g(x) 是通过 UCS 计算出来的从起始点到x点的最小花费值，

h(x) 是估算的从x点到目标状态的花费。

A* Tree Search, or simply known as A* Search, combines the strengths of uniform-cost search and greedy search. In this search, the heuristic is the summation of the cost in UCS, denoted by g(x), and the cost in the greedy search, denoted by h(x). The summed cost is denoted by f(x).

Heuristic: The following points should be noted wrt heuristics in A* search. 

• Here, h(x) is called the forward cost and is an estimate of the distance of the current node from the goal node.
• And, g(x) is called the backward cost and is the cumulative cost of a node from the root node.
• A* search is optimal only when for all nodes, the forward cost for a node h(x) underestimates the actual cost h*(x) to reach the goal. This property of A* heuristic is called admissibility. 

Admissibility:   

Strategy: Choose the node with the lowest f(x) value. 

 

A* Graph Search:

类似上面的搜索算法， 不同点事， 此算法可能扩展同一个节点多次。

• A* tree search works well, except that it takes time re-exploring the branches it has already explored. In other words, if the same node has expanded twice in different branches of the search tree, A* search might explore both of those branches, thus wasting time
• A* Graph Search, or simply Graph Search, removes this limitation by adding this rule: do not expand the same node more than once. 
• Heuristic. Graph search is optimal only when the forward cost between two successive nodes A and B, given by h(A) – h (B), is less than or equal to the backward cost between those two nodes g(A -> B). This property of the graph search heuristic is called consistency. 

Consistency:   

 

 

Dijkstra’s shortest path algorithm

https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/

最短路算法。

Given a graph and a source vertex in the graph, find the shortest paths from the source to all vertices in the given graph.
Dijkstra’s algorithm is very similar to Prim’s algorithm for minimum spanning tree. Like Prim’s MST, we generate a SPT (shortest path tree) with a given source as a root. We maintain two sets, one set contains vertices included in the shortest-path tree, other set includes vertices not yet included in the shortest-path tree. At every step of the algorithm, we find a vertex that is in the other set (set of not yet included) and has a minimum distance from the source.
Below are the detailed steps used in Dijkstra’s algorithm to find the shortest path from a single source vertex to all other vertices in the given graph.

 

Uniform-Cost Search (Dijkstra for large Graphs)

https://www.geeksforgeeks.org/uniform-cost-search-dijkstra-for-large-graphs/

对于有限节点图， 使用dijkstra没有问题。

对于节点图不是固定的情况，或者无限状态，或者很大的图，此算法使用。

Uniform-Cost Search is a variant of Dijikstra’s algorithm. Here, instead of inserting all vertices into a priority queue, we insert only source, then one by one insert when needed. In every step, we check if the item is already in priority queue (using visited array). If yes, we perform decrease key, else we insert it. 
This variant of Dijkstra is useful for infinite graphs and those graph which are too large to represent in the memory. Uniform-Cost Search is mainly used in Artificial Intelligence.

 

What is the difference between the uniform-cost search and Dijkstra's algorithm?

https://ai.stackexchange.com/questions/24668/what-is-the-difference-between-the-uniform-cost-search-and-dijkstras-algorithm

dijkstra -- 使用全部节点初始化队列

UCS --  使用开始节点初始化队列。

The answer to my question can be found in the paper Position Paper: Dijkstra's Algorithm versus Uniform Cost Search or a Case Against Dijkstra's Algorithm (2011), in particular section Similarities of DA and UCS, so you should read this paper for all the details.

DA and UCS are logically equivalent (i.e. they process the same vertices in the same order), but they do it differently. In particular, the main practical difference between the single-source DA and UCS is that, in DA, all nodes are initially inserted in a priority queue, while in UCS nodes are inserted lazily.

Here is the pseudocode (taken from the cited paper) of DA

Here is the pseudocode of the best-first search (BFS), of which UCS is just a particular case. Actually, this is the pseudocode of UCS where g(n)

is the cost of the path from the source node to n (although the title indicates that this is the pseudocode of BFS).