新“愚公移山”-- 动态规划

新“愚公移山”

http://go.helloworldroom.com:50080/problem/2721

 

题目描述

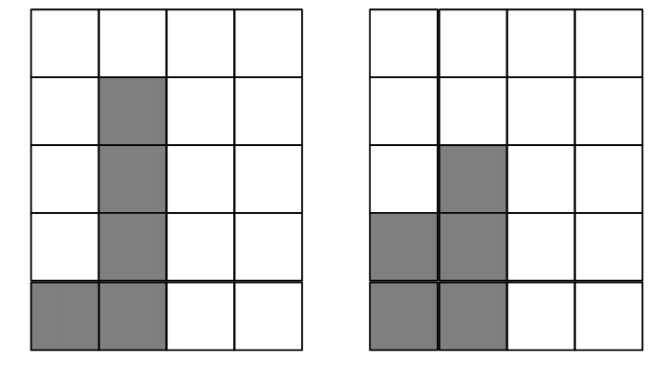
为了吸引中小学生，参观博物院不再停留在看和听，核心理念转变成了互动。新“愚公 移山”项目，屏幕上出现 n 个石块，屏幕下方的底盘是二维方格，每个方格恰好能放置一个 石块。石块放置的规则是：底盘每一竖行方格组成一列，必须从最左边的一列开始摆放，每 列从最下面的方格开始连续摆放积木，底盘至少要放两列，后一列放的积木数至少比前一列 多一个。n 个石块共有多少种摆放方案呢？ 下图为 5 个积木所能摆放的 2 种方案。

输入格式

一行，包含一个正整数 n，表示生成的石块个数。

输出格式

一行，包含一个数，表示按规则摆放石头的方案总数。

样例数据

input

5

output

2

对于 40%的数据满足 n≤10； 对于 80%的数据满足 n≤100； 对于 100%的数据满足 n≤200；

 

思路

 

解法

#include <bits/stdc++.h>
#include <vector>
#include <algorithm>
#include <deque>
#include <queue>
#include <string>
#include <set>
using namespace std;

int N;
int f[202][202] = {{0}};

int main() {
    cin >> N;

    // n rocks are in one column
    for (int n = 1; n <= N; n++) {
        f[n][1] = 1;
    }

    // 1 rock is with any number of columns
    for (int m = 2; m <= N; m++) {
        f[1][m] = 0;
    }

    // column is increasing
    for (int m = 2; m <= N; m++) {
        for (int n = 2; n <= N; n++) {
            f[n][m] = 0;


            int a1_max = n / m;
            for (int k = 1; k <= a1_max; k++) {
                int left_n = n - m * k;
                f[n][m] += f[left_n][m - 1];
            }
        }
    }

//    cout << endl;
//    cout << "----------------------------";
//    for (int n = 1; n <= N; n++) {
//        for (int m = 1; m <= N; m++) {
//            cout << f[n][m] << " ";
//        }
//        cout << endl;
//    }
//    cout << endl;

    int count = 0;
    for (int m = 2; m <= N; m++) {
//        cout << "m == " << m << " " << f[N][m] << endl;
        count += f[N][m];
    }

    cout << count << endl;
}

 

求总方案数的入门题 -- 容易理解

Count number of ways to reach destination in a Maze

https://www.geeksforgeeks.org/count-number-ways-reach-destination-maze/

Given a maze with obstacles, count the number of paths to reach the rightmost-bottommost cell from the topmost-leftmost cell. A cell in the given maze has a value of -1 if it is a blockage or dead-end, else 0.
From a given cell, we are allowed to move to cells (i+1, j) and (i, j+1) only.

Examples: 

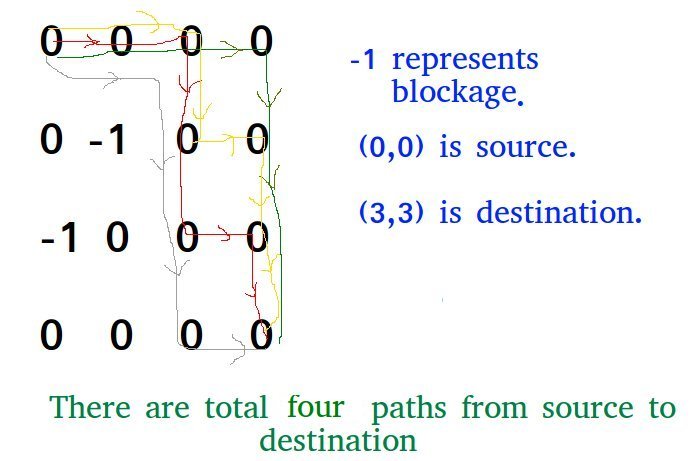
Input: maze[R][C] =  {{0,  0, 0, 0},
                      {0, -1, 0, 0},
                      {-1, 0, 0, 0},
                      {0,  0, 0, 0}};
Output: 4
There are four possible paths as shown in
below diagram.

 

 

 

// C++ program to count number of paths in a maze
// with obstacles.
#include<bits/stdc++.h>
using namespace std;
#define R 4
#define C 4

// Returns count of possible paths in a maze[R][C]
// from (0,0) to (R-1,C-1)
int countPaths(int maze[][C])
{
    // If the initial cell is blocked, there is no
    // way of moving anywhere
    if (maze[0][0]==-1)
        return 0;

    // Initializing the leftmost column
    for (int i=0; i<R; i++)
    {
        if (maze[i][0] == 0)
            maze[i][0] = 1;

        // If we encounter a blocked cell in leftmost
        // row, there is no way of visiting any cell
        // directly below it.
        else
            break;
    }

    // Similarly initialize the topmost row
    for (int i=1; i<C; i++)
    {
        if (maze[0][i] == 0)
            maze[0][i] = 1;

        // If we encounter a blocked cell in bottommost
        // row, there is no way of visiting any cell
        // directly below it.
        else
            break;
    }

    // The only difference is that if a cell is -1,
    // simply ignore it else recursively compute
    // count value maze[i][j]
    for (int i=1; i<R; i++)
    {
        for (int j=1; j<C; j++)
        {
            // If blockage is found, ignore this cell
            if (maze[i][j] == -1)
                continue;

            // If we can reach maze[i][j] from maze[i-1][j]
            // then increment count.
            if (maze[i-1][j] > 0)
                maze[i][j] = (maze[i][j] + maze[i-1][j]);

            // If we can reach maze[i][j] from maze[i][j-1]
            // then increment count.
            if (maze[i][j-1] > 0)
                maze[i][j] = (maze[i][j] + maze[i][j-1]);
        }
    }

    // If the final cell is blocked, output 0, otherwise
    // the answer
    return (maze[R-1][C-1] > 0)? maze[R-1][C-1] : 0;
}

// Driver code
int main()
{
    int maze[R][C] = {{0, 0, 0, 0},
                    {0, -1, 0, 0},
                    {-1, 0, 0, 0},
                    {0, 0, 0, 0}};
    cout << countPaths(maze);
    return 0;
}