计算PI -- 采用随机模拟方法

Buffon's Needle

https://mste.illinois.edu/activity/buffon/

介绍 + 模拟

Buffon's Needle is one of the oldest problems in the field of geometrical probability. It was first stated in 1777. It involves dropping a needle on a lined sheet of paper and determining the probability of the needle crossing one of the lines on the page. The remarkable result is that the probability is directly related to the value of pi.

This page will present an analytical solution to the problem along with a JavaScript applet for simulating the needle drop in the simplest case scenario in which the length of the needle is the same as the distance between the lines.

 

模拟

https://mfliedner.github.io/

 

原理解析

https://mp.weixin.qq.com/s?__biz=MzI1MjYyMTgwMg==&mid=2247483735&idx=1&sn=76c34e1960bacdb6462c5e7c23cba4ad&chksm=e9e1a7d2de962ec4c5aea0a710e6a08db625725fd13c328eb46caa0a011e7a06ccc53dc016c3&token=1777454829&lang=zh_CN#rd

 

直观的面积覆盖方法

https://www.mathsisfun.com/geometry/circle-area.html#:~:text=The%20area%20of%20a%20circle%20is%3A%20%CF%80%20%28Pi%29,3.14159...%20%3D%2028.27%20m2%20%28to%202%20decimal%20places%29

Comparing a Circle to a Square

It is interesting to compare the area of a circle to a square:

A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0.785398... = 78.5398...%

Why? Because the Square's Area is w²
and the Circle's Area is (π/4) × w²

 

推导

 

 

 

Code

https://github.com/fanqingsong/code_snippet/blob/master/CPP/calc_pi_rand.cpp

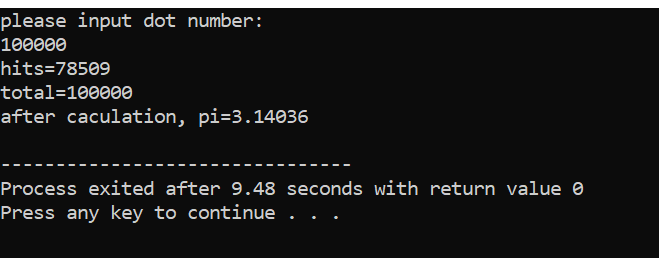
#include <iostream>
#include <iomanip>
#include <ctime>
#include <cmath>

using namespace std;

int main() {
    unsigned long long total = 0;
    unsigned long long hits = 0;
    double distance = 0;
    double pi = 0;
    double xpos = 0;
    double ypos = 0;

    srand((unsigned int)time(NULL));

    cout << "please input dot number:" << endl;
    cin >> total;

    for (unsigned long long i = 0; i < total; i++) {
        xpos = rand() / double(RAND_MAX);
        ypos = rand() / double(RAND_MAX);

        distance = sqrt(pow(xpos, 2) + pow(ypos, 2));
        if (distance <= 1) {
            hits++;
        }
    }

    cout << "hits=" << hits << endl;
    cout << "total=" << total << endl;

    pi = (double(hits) / total) * 4;

    cout << "after caculation, pi=" << pi << endl;
    return 0;
}

 

Demo