Unsupervised dimensionality reduction of sklearn
Unsupervised dimensionality reduction
https://scikit-learn.org/stable/modules/unsupervised_reduction.html
无监督学习领域的 维度约减 , 应对特征数目非常高的情况。 在监督学习步骤之前, 进行无监督学习,提取主要特征是, 非常有用的。
无监督模型 和 监督模型 可以使用pipeline进行串联。
If your number of features is high, it may be useful to reduce it with an unsupervised step prior to supervised steps. Many of the Unsupervised learning methods implement a
transformmethod that can be used to reduce the dimensionality. Below we discuss two specific example of this pattern that are heavily used.Pipelining
The unsupervised data reduction and the supervised estimator can be chained in one step. See Pipeline: chaining estimators.
PCA: principal component analysis
PCA寻找到一组特征,能够很好地捕获到原始特征的方差。
decomposition.PCAlooks for a combination of features that capture well the variance of the original features. See Decomposing signals in components (matrix factorization problems).
https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html#sklearn.decomposition.PCA
PCA 是一种线性维度约减方法, 使用奇异值分解, 投射数据到更低的维度。
输入数据需要中心化,但是不需要伸缩, 然后应用SVD。
此接口不支持稀疏数据, 使用 TruncatedSVD 处理稀疏输入。
Principal component analysis (PCA).
Linear dimensionality reduction using Singular Value Decomposition of the data to project it to a lower dimensional space. The input data is centered but not scaled for each feature before applying the SVD.
It uses the LAPACK implementation of the full SVD or a randomized truncated SVD by the method of Halko et al. 2009, depending on the shape of the input data and the number of components to extract.
It can also use the scipy.sparse.linalg ARPACK implementation of the truncated SVD.
Notice that this class does not support sparse input. See
TruncatedSVDfor an alternative with sparse data.
>>> import numpy as np >>> from sklearn.decomposition import PCA >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) >>> pca = PCA(n_components=2) >>> pca.fit(X) PCA(n_components=2) >>> print(pca.explained_variance_ratio_) [0.9924... 0.0075...] >>> print(pca.singular_values_) [6.30061... 0.54980...]
TruncatedSVD
https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.TruncatedSVD.html#sklearn.decomposition.TruncatedSVD
维度约减使用 裁剪的SVD。执行线性维度约减, 通过裁剪奇异值分解。
与PCA不同,此模型不需要中心化数据, 对于系数数据非常高效。
应用在文本分析领域, 被称为LSA,浅层语义分析。
Dimensionality reduction using truncated SVD (aka LSA).
This transformer performs linear dimensionality reduction by means of truncated singular value decomposition (SVD). Contrary to PCA, this estimator does not center the data before computing the singular value decomposition. This means it can work with sparse matrices efficiently.
In particular, truncated SVD works on term count/tf-idf matrices as returned by the vectorizers in
sklearn.feature_extraction.text. In that context, it is known as latent semantic analysis (LSA).This estimator supports two algorithms: a fast randomized SVD solver, and a “naive” algorithm that uses ARPACK as an eigensolver on
X * X.TorX.T * X, whichever is more efficient.
>>> from sklearn.decomposition import TruncatedSVD >>> from scipy.sparse import random as sparse_random >>> X = sparse_random(100, 100, density=0.01, format='csr', ... random_state=42) >>> svd = TruncatedSVD(n_components=5, n_iter=7, random_state=42) >>> svd.fit(X) TruncatedSVD(n_components=5, n_iter=7, random_state=42) >>> print(svd.explained_variance_ratio_) [0.0646... 0.0633... 0.0639... 0.0535... 0.0406...] >>> print(svd.explained_variance_ratio_.sum()) 0.286... >>> print(svd.singular_values_) [1.553... 1.512... 1.510... 1.370... 1.199...]
PCA是基于variance的分解
https://paradiseeee.github.io/2019/02/21/Python-DataScience-CookBook-Learning-Notes-(I)/
从此得知, PCA是首先计算 特征的相关矩阵, 然后对相关矩阵, 做SVD分解, 分析后的奇异值,选择前面较大的两个, 并获得对应的特征向量, 对原始特征做变换。
从此可以看出, PCA关注的是特征相关性差异度。将最大差异的特征保留下来。
- 对于多变量问题,进行 PCA 降维只有很小的信息损失。
- 对于一维数据,使用方差衡量数据的变异情况;对于多维数据,使用协方差矩阵。
- 示例:在 iris 数据集上进行 PCA 降维:
- 数据标准化:均值为 0,方差为 1
- 计算数据的相关矩阵和单位标准差偏差值
- 将相关矩阵分解成特征向量和特征值
- 根据特征值的大小,选择 Top-N 个特征向量
- 投射特征向量矩阵到一个新的子空间
- 选取特征值的标准:
- 特征值标准:特征值为 1,意味至少可以解释一个变量,至少为 1 才能选取
- 变异解释比 PVE:一般以累计值为标准,从 Top-N 主成分累计到接近 100%
import scipy from sklearn.datasets import load_iris from sklearn.preprocessing import scale import pandas as pd # iris 数据集:3个分类,4维特征 iris = load_iris() X, Y = iris['data'], iris['target'] print("---------- X ------------") print(X) print("---------- Y ------------") print(Y) # 标准化:由于 PCA 为无监督方法,只需标准化 features x_s = scale(X, with_mean=True, with_std=True, axis=0) print("---------- x_s ------------") print(x_s) # 计算相关矩阵: x_corr = np.corrcoef(x_s.T) print("---------- x_corr ------------") print(x_corr) # 从相关矩阵中计算特征值和特征向量: eigenvalue, right_eigenvector = scipy.linalg.eig(x_corr) print("---------- eigenvalue ------------") print(eigenvalue) print("---------- right_eigenvector ------------") print(right_eigenvector) # 选择 Top-2 特征向量(eig 函数输出降序排列) w = right_eigenvector[:, 0:2] print("---------- w ------------") print(w) # 使用特征向量作为权重进行PCA降维(投影到特征向量方向) x_rd = x_s.dot(w) print("----------x_rd ------------") print(x_rd) # 画出新的特征空间的散点图 plt.figure(facecolor='#ffffff') plt.scatter(x_rd[:,0], x_rd[:,1], c=Y) plt.xlabel('Component 1') plt.ylabel('Component 2') plt.show() # 按照变准选取特征值 df = pd.DataFrame( np.random.randn(4,3), columns=['Eigen Values', 'PVEs', 'Cummulative PVE'], index=pd.Index([1,2,3,4], name='Principal Component') ) cum_pct, var_pct = 0, 0 for i, eigval in enumerate(eigenvalue): var_pct = round((eigval / len(eigenvalue)), 3) cum_pct += var_pct df['Eigen Values'][i+1] = eigval df['PVEs'][i+1] = var_pct df['Cummulative PVE'][i+1] = cum_pct df.plot() plt.show() # 可以看到前两个主成分解释了 95.9% 的变异
奇异值分解(SVD)
https://zhuanlan.zhihu.com/p/29846048
此文对SVD原理介绍的非常清楚, 建议参考。
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结,并讨论在在PCA降维算法中是如何运用运用SVD的。
https://www.cnblogs.com/cxq1126/p/13407279.html
下面是numpy中线性代数包中提供的 svd分解样例。
import numpy as np import matplotlib.pyplot as plt plt.style.use('ggplot') words =['I', 'like', 'enjoy', 'deep', 'learning', 'NLP', 'flying','.'] X = np.array([[0,2,1,0,0,0,0,0], #X是共现矩阵 [2,0,0,1,0,1,0,0], [1,0,0,0,0,0,1,0], [0,1,0,0,1,0,0,0], [0,0,0,1,0,0,0,1], [0,1,0,0,0,0,0,1], [0,0,1,0,0,0,0,1], [0,0,0,0,1,1,1,0]]) U, s, Vh = np.linalg.svd(X, full_matrices=False) print(U.shape) #(8, 8) print(s.shape) #(8,) print(Vh.shape) #(8, 8) print(np.allclose(X, np.dot(U * s, Vh))) #True,allclose比较两个array是不是每一元素都相等,默认在1e-05的误差范围内 plt.xlim([-0.8, 0.2]) plt.ylim([-0.8, 0.8]) for i in range(len(words)): plt.text(U[i,0], U[i,1], words[i])
Random projections
The module:
random_projectionprovides several tools for data reduction by random projections. See the relevant section of the documentation: Random Projection.
https://scikit-learn.org/stable/modules/random_projection.html#random-projection
随机映射是简单并且计算上高效的 维度约减算法, 可以平很可控的精确度 和 更小的模型体积。
随机映射有两种 目标分布空间, 高斯随机分布 和 稀疏随机分布。
随机映射的 维度和分布式可以控制的, 为了保存数据集中任何两个样本之间的两两距离。 适用于基于距离的逼近技术。
The
sklearn.random_projectionmodule implements a simple and computationally efficient way to reduce the dimensionality of the data by trading a controlled amount of accuracy (as additional variance) for faster processing times and smaller model sizes. This module implements two types of unstructured random matrix: Gaussian random matrix and sparse random matrix.The dimensions and distribution of random projections matrices are controlled so as to preserve the pairwise distances between any two samples of the dataset. Thus random projection is a suitable approximation technique for distance based method.
GaussianRandomProjection
https://scikit-learn.org/stable/modules/generated/sklearn.random_projection.GaussianRandomProjection.html#sklearn.random_projection.GaussianRandomProjection
Reduce dimensionality through Gaussian random projection.
The components of the random matrix are drawn from N(0, 1 / n_components).
>>> import numpy as np >>> from sklearn.random_projection import GaussianRandomProjection >>> rng = np.random.RandomState(42) >>> X = rng.rand(100, 10000) >>> transformer = GaussianRandomProjection(random_state=rng) >>> X_new = transformer.fit_transform(X) >>> X_new.shape (100, 3947)
用随机映射进行数据降维
https://paradiseeee.github.io/2019/02/21/Python-DataScience-CookBook-Learning-Notes-(I)/
PCA 和 SVD 的运算代价高昂,随机映射方法运算速度更快。根据 Johnson-Linden Strauss 定理的推论,从高维到低维的 Euclidean Space 的映射是存在的,可以使点到点的距离保持在一个 epsilon 的方差内。随机映射的目的就是保持任意两点之间的距离,同时降低数据的维度。
from sklearn.metrics import euclidean_distances from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.random_projection import GaussianRandomProjection # 处理 20 个新闻组的文本数据,采用高斯随机映射 # 高斯随机矩阵是从正态分布 N(0, 1000^-1) 中采样生成的,1000是结果的维度 # 使用 sci.crypt 分类,将文本数据转换为向量表示 data = fetch_20newsgroups(categories=['alt.atheism']) # 下载完会本地化,储存进 sklearn 模块 # 从 data 中创建一个 词-文档 矩阵,词频作为值 vectorizer = TfidfVectorizer(use_idf=False) vector = vectorizer.fit_transform(data.data) print(f'The Dimension of Original Data: {vector.shape}') # 使用随机映射降维到 1000 维 gauss_proj = GaussianRandomProjection(n_components=1000) gauss_proj.fit(vector) # 将原始数据转换到新的空间 vector_t = gauss_proj.transform(vector) print(f'The Dimension of Transformed Data: {vector_t.shape}') # 检验是否保持了数据点的距离 org_dist = euclidean_distances(vector) red_dist = euclidean_distances(vector_t) diff_dist = abs(org_dist - red_dist) # 上面的 diff_dist 返回一个 n x n 方阵,绘制成热力图: plt.figure(figsize=(8, 8)) plt.pcolor(diff_dist[0:100, 0:100]) plt.colorbar() plt.show()
euclidean_distances
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.pairwise.euclidean_distances.html
Considering the rows of X (and Y=X) as vectors, compute the distance matrix between each pair of vectors.
For efficiency reasons, the euclidean distance between a pair of row vector x and y is computed as:
dist(x, y) = sqrt(dot(x, x) - 2 * dot(x, y) + dot(y, y))This formulation has two advantages over other ways of computing distances. First, it is computationally efficient when dealing with sparse data. Second, if one argument varies but the other remains unchanged, then
dot(x, x)and/ordot(y, y)can be pre-computed.However, this is not the most precise way of doing this computation, because this equation potentially suffers from “catastrophic cancellation”. Also, the distance matrix returned by this function may not be exactly symmetric as required by, e.g.,
scipy.spatial.distancefunctions.
>>> from sklearn.metrics.pairwise import euclidean_distances >>> X = [[0, 1], [1, 1]] >>> # distance between rows of X >>> euclidean_distances(X, X) array([[0., 1.], [1., 0.]]) >>> # get distance to origin >>> euclidean_distances(X, [[0, 0]]) array([[1. ], [1.41421356]])
Feature agglomeration
特征凝结,使用层次聚类来分组表现相似的特征。
cluster.FeatureAgglomerationapplies Hierarchical clustering to group together features that behave similarly.
FeatureAgglomeration
Agglomerate features.
Similar to AgglomerativeClustering, but recursively merges features instead of samples.
>>> import numpy as np >>> from sklearn import datasets, cluster >>> digits = datasets.load_digits() >>> images = digits.images >>> X = np.reshape(images, (len(images), -1)) >>> agglo = cluster.FeatureAgglomeration(n_clusters=32) >>> agglo.fit(X) FeatureAgglomeration(n_clusters=32) >>> X_reduced = agglo.transform(X) >>> X_reduced.shape (1797, 32)
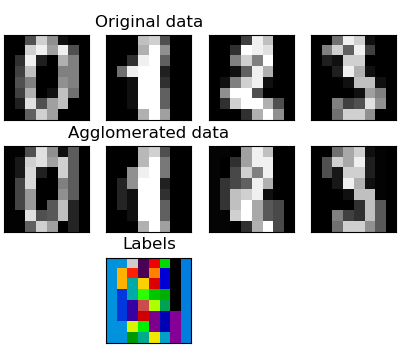
Feature agglomeration -- demo
https://scikit-learn.org/stable/auto_examples/cluster/plot_digits_agglomeration.html#sphx-glr-auto-examples-cluster-plot-digits-agglomeration-py
对图片进行特征凝结,然后还原。
These images how similar features are merged together using feature agglomeration.
print(__doc__) # Code source: Gaël Varoquaux # Modified for documentation by Jaques Grobler # License: BSD 3 clause import numpy as np import matplotlib.pyplot as plt from sklearn import datasets, cluster from sklearn.feature_extraction.image import grid_to_graph digits = datasets.load_digits() images = digits.images X = np.reshape(images, (len(images), -1)) connectivity = grid_to_graph(*images[0].shape) agglo = cluster.FeatureAgglomeration(connectivity=connectivity, n_clusters=32) agglo.fit(X) X_reduced = agglo.transform(X) X_restored = agglo.inverse_transform(X_reduced) images_restored = np.reshape(X_restored, images.shape) plt.figure(1, figsize=(4, 3.5)) plt.clf() plt.subplots_adjust(left=.01, right=.99, bottom=.01, top=.91) for i in range(4): plt.subplot(3, 4, i + 1) plt.imshow(images[i], cmap=plt.cm.gray, vmax=16, interpolation='nearest') plt.xticks(()) plt.yticks(()) if i == 1: plt.title('Original data') plt.subplot(3, 4, 4 + i + 1) plt.imshow(images_restored[i], cmap=plt.cm.gray, vmax=16, interpolation='nearest') if i == 1: plt.title('Agglomerated data') plt.xticks(()) plt.yticks(()) plt.subplot(3, 4, 10) plt.imshow(np.reshape(agglo.labels_, images[0].shape), interpolation='nearest', cmap=plt.cm.nipy_spectral) plt.xticks(()) plt.yticks(()) plt.title('Labels') plt.show()
使用 NMF 分解特征矩阵
前文使用主成分分析和矩阵分解技术进行降维,Non-negative Matrix Factorization(NMF)采用协同过滤算法进行降维。
用于协同过滤的推荐算法。
from collections import defaultdict from sklearn.decomposition import NMF import numpy as np import matplotlib.pyplot as plt # 数据集:电影影评数据 ratings = [ [5., 5., 4.5, 4.5, 5., 3., 2., 2., 0., 0.], [4.2, 4.7, 5., 3.7, 3.5, 0., 2.7, 2., 1.9, 0.], [2.5, 0., 3.3, 3.4, 2.2, 4.6, 4., 4.7, 4.2, 3.6], [3.8, 4.1, 4.6, 4.5, 4.7, 2.2, 3.5, 3., 2.2, 0.], [2.1, 2.6, 0., 2.1, 0., 3.8, 4.8, 4.1, 4.3, 4.7], [4.7, 4.5, 0., 4.4, 4.1, 3.5, 3.1, 3.4, 3.1, 2.5], [2.8, 2.4, 2.1, 3.3, 3.4, 3.8, 4.4, 4.9, 4.0, 4.3], [4.5, 4.7, 4.7, 4.5, 4.9, 0., 2.9, 2.9, 2.5, 2.1], [0., 3.3, 2.9, 3.6, 3.1, 4., 4.2, 0.0, 4.5, 4.6], [4.1, 3.6, 3.7, 4.6, 4., 2.6, 1.9, 3., 3.6, 0.] ] movie_dict = { 1: 'Star Wars', 2: 'Matrix', 3: 'Inception', 4: 'Harry Potter', 5: 'The hobbit', 6: 'Guns of Navarone', 7: 'Saving Private Ryan', 8: 'Enemy at the gates', 9: 'Where eagles dare', 10: 'Great Escape' } # 以下是模拟推荐系统的问题,通过用户对电影的评分,预测未知电影的评分。 A = np.asmatrix(ratings, dtype=float) print("------------ A ---------------") print(A) nmf = NMF(n_components=2, random_state=1) A_dash = nmf.fit_transform(A) print("------------ A_dash ---------------") print(A_dash) # 检查降维后的矩阵 for i in range(A_dash.shape[0]): print( "User id = {}, comp_1 score = {}, comp_2 score = {}".format( i+1, A_dash[i][0], A_dash[i][1] )) plt.figure(figsize=(5,5)) plt.title("User Concept Mapping") plt.scatter(A_dash[:,0], A_dash[:,1]) plt.xlabel("Component 1 Score"); plt.ylabel("Component 2 Score") plt.show() # 检查成分矩阵 F = nmf.components_ print("------------ F ---------------") print(F) plt.figure(figsize=(5,5)) plt.title("Movie Concept Mapping") plt.scatter(F[0,:], F[1,:]) plt.xlabel("Component 1 Score"); plt.ylabel("Component 2 Score") for i in range(F[0,:].shape[0]): plt.annotate(movie_dict[i+1], (F[0,:][i], F[1,:][i])) plt.show()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号