naive bayes of sklearn

naive bayes

首先贝叶斯定理是定义目标分类和依赖特征之间的概率转换关系的原理。

其次naive是朴素的意思，依赖的特征可能是多个，但是多个特征之间可能依赖，朴素的含义，是假设这些特征的依赖是不存在的。

朴素贝叶斯在实际应用中效果很好，尽管特征之间是存在依赖关系的。

reference：

https://scikit-learn.org/stable/modules/naive_bayes.html

略

http://www.imooc.com/article/259855

朴素贝叶斯算法是在贝叶斯公式的基础之上演化而来的分类算法，在机器学习中有着广泛的应用。朴素贝叶斯算法是条件化的贝叶斯算法，即在特征条件独立假说下的贝叶斯算法。

https://www.leiphone.com/news/201707/VyUNGYnEy3kXnkVb.html

1、贝叶斯定理

假设对于某个数据集，随机变量C表示样本为C类的概率，F1表示测试样本某特征出现的概率，套用基本贝叶斯公式，则如下所示：

上式表示对于某个样本，特征F1出现时，该样本被分为C类的条件概率。那么如何用上式来对测试样本分类呢？

举例来说，有个测试样本，其特征F1出现了（F1=1），那么就计算P(C=0|F1=1)和P(C=1|F1=1)的概率值。前者大，则该样本被认为是0类；后者大，则分为1类。

对该公示，有几个概念需要熟知：

先验概率（Prior）。P(C)是C的先验概率，可以从已有的训练集中计算分为C类的样本占所有样本的比重得出。

证据（Evidence）。即上式P(F1)，表示对于某测试样本，特征F1出现的概率。同样可以从训练集中F1特征对应样本所占总样本的比例得出。

似然（likelihood）。即上式P(F1|C)，表示如果知道一个样本分为C类，那么他的特征为F1的概率是多少。

对于多个特征而言，贝叶斯公式可以扩展如下：

分子中存在一大串似然值。当特征很多的时候，这些似然值的计算是极其痛苦的。现在该怎么办？

2、朴素的概念

为了简化计算，朴素贝叶斯算法做了一假设：“朴素的认为各个特征相互独立”。这么一来，上式的分子就简化成了：

P(C)P(F1|C)P(F2|C)...P(Fn|C)。

这样简化过后，计算起来就方便多了。

这个假设是认为各个特征之间是独立的，看上去确实是个很不科学的假设。因为很多情况下，各个特征之间是紧密联系的。然而在朴素贝叶斯的大量应用实践实际表明其工作的相当好。

例子

http://www.imooc.com/article/259855

例子如下，

网页上有详细的计算讲解过程，用于理解计算过程。

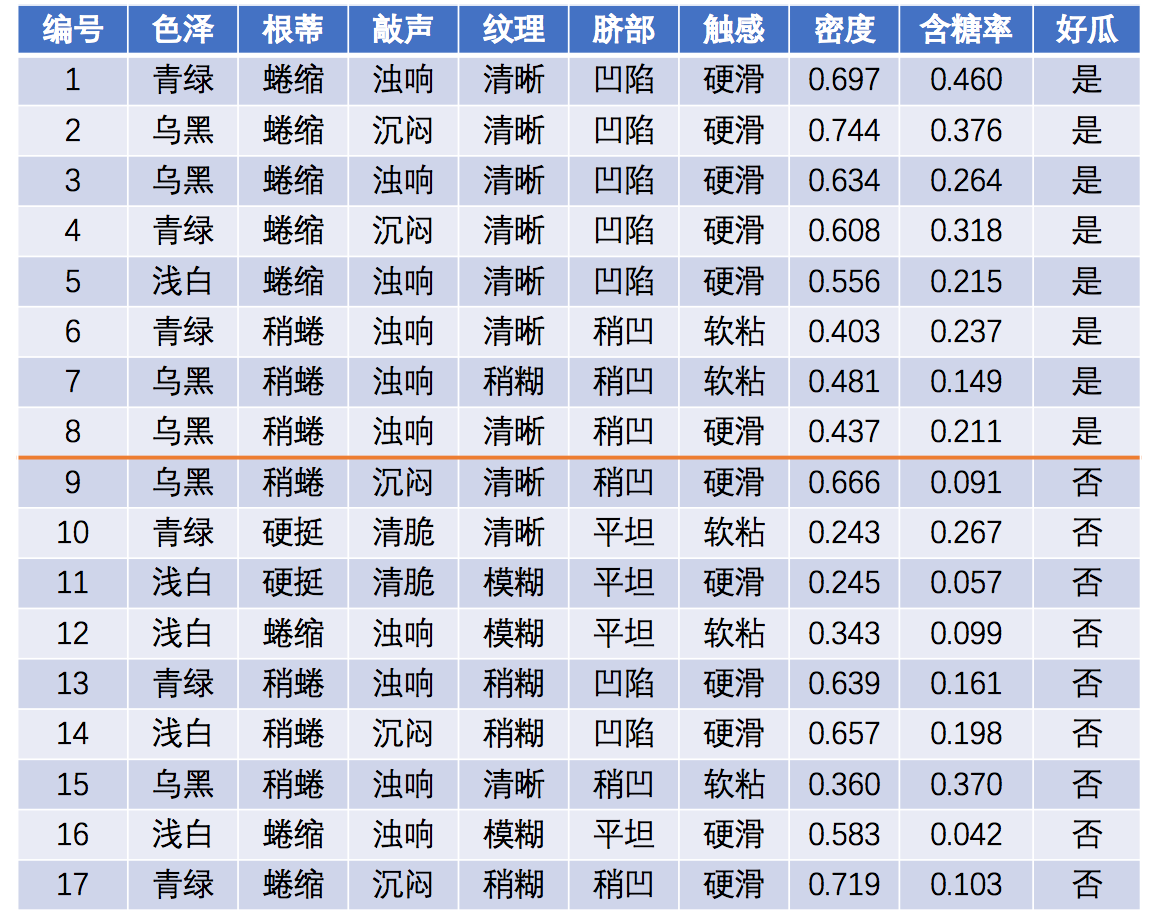
历史数据

预测样本

如何工作的？

https://www.datacamp.com/community/tutorials/naive-bayes-scikit-learn

从中可以看出，根据训练数据计算先验概率和条件概率（后验概率，已知结果，统计各个条件值的似然概率）是模型部分。

然后计算已知某些条件值得情况下，产生分类的似然概率。

First Approach (In case of a single feature)

Naive Bayes classifier calculates the probability of an event in the following steps:

Step 1: Calculate the prior probability for given class labels

Step 2: Find Likelihood probability with each attribute for each class

Step 3: Put these value in Bayes Formula and calculate posterior probability.

Step 4: See which class has a higher probability, given the input belongs to the higher probability class.

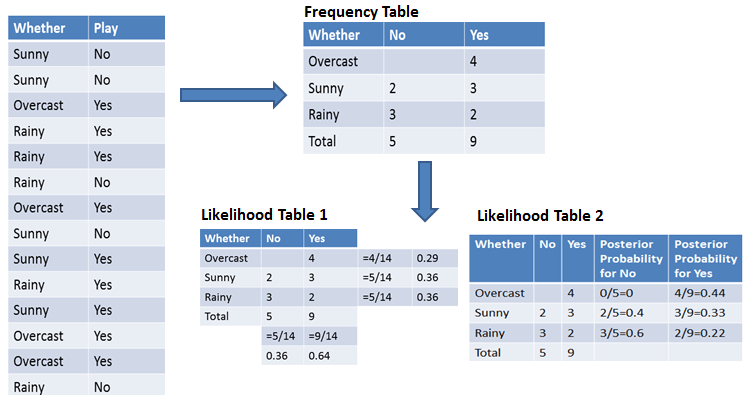
For simplifying prior and posterior probability calculation you can use the two tables frequency and likelihood tables. Both of these tables will help you to calculate the prior and posterior probability. The Frequency table contains the occurrence of labels for all features. There are two likelihood tables. Likelihood Table 1 is showing prior probabilities of labels and Likelihood Table 2 is showing the posterior probability.

Now suppose you want to calculate the probability of playing when the weather is overcast.

Probability of playing:

P(Yes | Overcast) = P(Overcast | Yes) P(Yes) / P (Overcast) .....................(1)

Calculate Prior Probabilities:

P(Overcast) = 4/14 = 0.29

P(Yes)= 9/14 = 0.64

Calculate Posterior Probabilities:

P(Overcast |Yes) = 4/9 = 0.44

Put Prior and Posterior probabilities in equation (1)

P (Yes | Overcast) = 0.44 * 0.64 / 0.29 = 0.98(Higher)

Similarly, you can calculate the probability of not playing:

Probability of not playing:

P(No | Overcast) = P(Overcast | No) P(No) / P (Overcast) .....................(2)

Calculate Prior Probabilities:

P(Overcast) = 4/14 = 0.29

P(No)= 5/14 = 0.36

Calculate Posterior Probabilities:

P(Overcast |No) = 0/9 = 0

Put Prior and Posterior probabilities in equation (2)

P (No | Overcast) = 0 * 0.36 / 0.29 = 0

The probability of a 'Yes' class is higher. So you can determine here if the weather is overcast than players will play the sport.

基于贝叶斯的单词拼写错误检测

http://www.imooc.com/article/259855

import re, collections
 
def words(text): return re.findall('[a-z]+', text.lower()) 
 
def train(features):
    model = collections.defaultdict(lambda: 1)
    for f in features:
        model[f] += 1
    return model
 
NWORDS = train(words(open('big.txt').read()))
 
alphabet = 'abcdefghijklmnopqrstuvwxyz'
 
def edits1(word):
    n = len(word)
    return set([word[0:i]+word[i+1:] for i in range(n)] +                     # deletion
               [word[0:i]+word[i+1]+word[i]+word[i+2:] for i in range(n-1)] + # transposition
               [word[0:i]+c+word[i+1:] for i in range(n) for c in alphabet] + # alteration
               [word[0:i]+c+word[i:] for i in range(n+1) for c in alphabet])  # insertion
 
def known_edits2(word):
    return set(e2 for e1 in edits1(word) for e2 in edits1(e1) if e2 in NWORDS)
 
def known(words): return set(w for w in words if w in NWORDS)
 
def correct(word):
    candidates = known([word]) or known(edits1(word)) or known_edits2(word) or [word]
    return max(candidates, key=lambda w: NWORDS[w])


#appl #appla #learw #tess #morw
correct('teal')

自动分析评价给评级

https://www.leiphone.com/news/201707/VyUNGYnEy3kXnkVb.html

https://github.com/RobTomb/pac_ai/blob/master/code/sentimentNaiveBayes.py

import os
from jieba import posseg as pseg
import pandas as pd



def getP(word,NBDict,flag):

    if(word in NBDict):
        return NBDict[word][flag]+1
    else:    
        return 1

def classify(wordsTest,NBDict):
    p0=p1=p2=1
    for words in wordsTest:
        print(words[0])
        print(p0,p1,p2)
        p0*=getP(words[0],NBDict,0)/(NBDict['evalation'][0]+len(wordsTest))
        p1*=getP(words[0],NBDict,1)/(NBDict['evalation'][1]+len(wordsTest))
        p2*=getP(words[0],NBDict,2)/(NBDict['evalation'][2]+len(wordsTest))
    p0*=NBDict['evalation'][0]/sum(NBDict['evalation'])
    p1*=NBDict['evalation'][1]/sum(NBDict['evalation'])
    p2*=NBDict['evalation'][2]/sum(NBDict['evalation'])
    p=[p0,p1,p2]
    return p.index(max(p))




def countNum(wordsList,trainSet):
    #print(wordsList,trainSet)
    NBDict={'evalation':[0,0,0]}
    for ix in trainSet.index:
        flag = trainSet.ix[ix,'pos_se_tag']
        NBDict['evalation'][flag]+=1
        for words in wordsList[ix]:
            if(words[0] in NBDict):
                NBDict[words[0]][flag]+=1
            else:
                NBDict[words[0]] = [0,0,0]
                NBDict[words[0]][flag]=1

    #print(NBDict)
    return NBDict



def tagTrainSet(trainSet):
    trainSet['pos_se_tag'] = 0
    for ix in trainSet.index:
        if(trainSet.ix[ix,'pos_se'] == '好'):
            trainSet.ix[ix,'pos_se_tag'] = 0

        elif(trainSet.ix[ix,'pos_se'] == '中'):
            trainSet.ix[ix,'pos_se_tag'] = 1

        elif(trainSet.ix[ix,'pos_se'] == '差'):
            trainSet.ix[ix,'pos_se_tag'] = 2


#def cutParagraphToWords(pa):

def getF(trainSet):
    dataSet=trainSet['content']
    wordsList=[]        
    for paragraph in dataSet.values:
        wordsList.append(cutParagraphToWords(paragraph))
    return wordsList

def cutParagraphToWords(paragraph):
    #print('step 1 cut paragraph to words')
    stopStrFileName='stopStr.txt'
    stopPath='{0}/dict/{1}'.format(os.path.dirname(os.getcwd()),stopStrFileName)

    with open(stopPath,'r') as stopStrFile:
        stopWords=stopStrFile.read().split(' ')

    wordsCutList=[]
    paragraphToWords=pseg.cut(paragraph.split('>').pop())
    
    for word,flag in paragraphToWords:
        if(word not in stopWords and word != ' ' and word != ''):    
            wordsCutList.append([word,flag])
    return wordsCutList





def main():
    dataFileName='data11.xlsx'
    dataFilePath='{0}/NaiveBayesData/{1}'.format(os.path.dirname(os.getcwd()),dataFileName)
    trainSet=pd.read_excel(dataFilePath)
    #print(trainSet)
    wordsList=getF(trainSet)    
    tagTrainSet(trainSet)
    NBDict=countNum(wordsList,trainSet)
    p=classify([['差', 'a'], ['连单', 'a']],NBDict)
    print('ae: %d' % p)


if __name__ == '__main__':
    main()

sklearn API

https://scikit-learn.org/stable/modules/classes.html?highlight=bayes#module-sklearn.naive_bayes

高斯贝叶斯接口面向连续性特征 -- 例如鸢尾花分类

Category接口面向离散型特征

贝努力接口面向真假型特征

The sklearn.naive_bayes module implements Naive Bayes algorithms. These are supervised learning methods based on applying Bayes’ theorem with strong (naive) feature independence assumptions.

User guide: See the Naive Bayes section for further details.

naive_bayes.BernoulliNB(*[, alpha, …])

Naive Bayes classifier for multivariate Bernoulli models.

naive_bayes.CategoricalNB(*[, alpha, …])

Naive Bayes classifier for categorical features

naive_bayes.ComplementNB(*[, alpha, …])

The Complement Naive Bayes classifier described in Rennie et al.

naive_bayes.GaussianNB(*[, priors, …])

Gaussian Naive Bayes (GaussianNB)

naive_bayes.MultinomialNB(*[, alpha, …])

Naive Bayes classifier for multinomial models

https://scikit-learn.org/stable/modules/naive_bayes.html

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
print("Number of mislabeled points out of a total %d points : %d"
      % (X_test.shape[0], (y_test != y_pred).sum()))

https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.CategoricalNB.html#sklearn.naive_bayes.CategoricalNB

import numpy as np
rng = np.random.RandomState(1)
X = rng.randint(5, size=(6, 100))
y = np.array([1, 2, 3, 4, 5, 6])
from sklearn.naive_bayes import CategoricalNB
clf = CategoricalNB()
clf.fit(X, y)

print(clf.predict(X[2:3]))

posted @ 2020-12-16 17:06 lightsong 阅读(174) 评论(0) 编辑收藏举报

刷新页面返回顶部

Stay Hungry,Stay Foolish!

lightsong

{Web: [React, Vue, NodeJS, HTTP]，DevOps:[Jenkins,Docker,K8S], Languages:[Python, JS, C, Lua, Shell, Groovy]}

naive bayes of sklearn

naive bayes

1、贝叶斯定理

2、朴素的概念

例子

如何工作的？

First Approach (In case of a single feature)

基于贝叶斯的单词拼写错误检测

自动分析评价给评级

sklearn API

公告

`naive_bayes.BernoulliNB`(*[, alpha, …])	Naive Bayes classifier for multivariate Bernoulli models.
`naive_bayes.CategoricalNB`(*[, alpha, …])	Naive Bayes classifier for categorical features
`naive_bayes.ComplementNB`(*[, alpha, …])	The Complement Naive Bayes classifier described in Rennie et al.
`naive_bayes.GaussianNB`(*[, priors, …])	Gaussian Naive Bayes (GaussianNB)
`naive_bayes.MultinomialNB`(*[, alpha, …])	Naive Bayes classifier for multinomial models