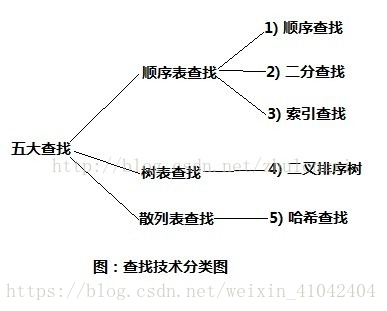
五大查找

一、顺序查找：

顺序查找的原理很简单，就是遍历整个列表，逐个进行记录的关键字与给定值比较，若某个记录的关键字和给定值相等，则查找成功，找到所查的记录。如果直到最后一个记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找失败。

public static int SequenceSearch(int[] arr, int key)
{
for (int i = 0; i < arr.Length; i++)
{
if (arr[i] == key)
{
return i;
}
}
return -1;
}

二、折半查找（二分查找）：

时间复杂度为O(LogN)。

二分查找的基本思想是，在有序表中，取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续查找；若给定值大于中间记录的关键字，则在中间记录的右半区继续查找。不断重复上述过程，直到找到为止。

从二分查找的定义我们可以看出，使用二分查找有两个前提条件：

1，待查找的列表必须有序。

2，必须使用线性表的顺序存储结构来存储数据。

public static int BinarySearch(int[] arr, int key,int low,int high)
{
while (low <= high)
{
int middle = (low + high) / 2;
//判断中间记录是否与给定值相等
if (key == arr[middle])
return middle;
else
{
// 在中间记录的左半区查找
if (key < arr[middle])
high = middle - 1;
// 在中间记录的左半区查找
else
low = middle + 1;
}
}
return -1;
}

三、分块查找（索引顺序查找）：

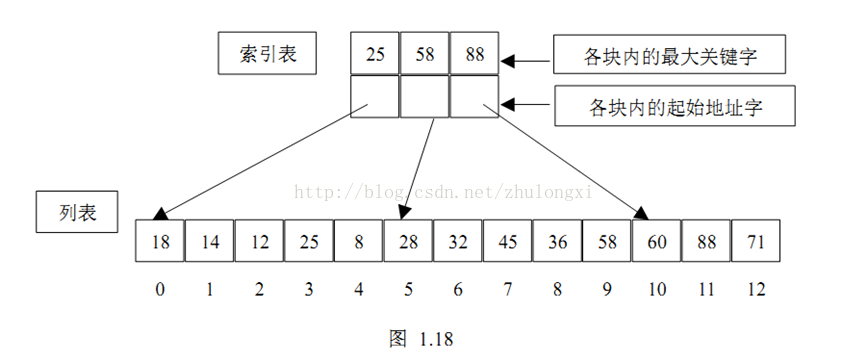
索引查找又称为分块查找，是一种介于顺序查找和二分查找之间的一种查找方法，

分块查找的基本思想是：分块查找把线性表分成若干块，每块中的元素存储顺序是任意的，但是块与块之间必须按照关键字大小有序排列，即前一块中的最大关键字要小于后一块中的最小关键字。对顺序表进行分块查找需要额外建立一个索引表，表中的每一项对应线性表中的一块，每个索引项都有键值分量和链值分量，键值分量存放对应块的最大关键字，链值分量存放指向本块第一个元素和最后一个元素的指针（即在数组中的下标）。显然索引表中的所有索引项都是按照其关键字递增顺序排列的。

首先查找索引表，可用二分查找或顺序查找，然后在确定的块中进行顺序查找。

/// <summary>
/// 分块
/// </summary>
/// <param name="arr"></param>
///<param name="blockSize">每块大小</param>
/// <returns></returns>
public static IndexItem[] DividBlock(int[] arr, int blockSize)
{
int totalBlock = (int)Math.Ceiling(arr.Length * 1.0 / blockSize);//块的总数
IndexItem[] blocks = new IndexItem[totalBlock];
//确定每一块的信息
int j = 0;//数组的索引
int k = 0;
int s = 0;
for (int i = 0; i < totalBlock; i++)
{
s = j * blockSize;
k = s + blockSize - 1;
blocks[i].start = s;
if (k>arr.Length - 1)
{
k = arr.Length - 1;
}
blocks[i].end = k;
blocks[i].key = arr[k];
j++;
}
return blocks;
}
public static int IndexSearch(int[] arr,int key,int blockSize)
{
IndexItem[] indexItem = DividBlock(arr, blockSize);//对数组进行分块，得到索引列表
int i=0;
while (i < indexItem.Length && key > indexItem[i].key)//从索引列表中查找key所在的索引列表
{
i++;
}
if (i >= indexItem.Length)
return -1;
int j = indexItem[i].start;
int k = indexItem[i].end;
for (int l = j ; l <=k; l++)//根据key所在的索引列表的索引进行顺序查找key在数组中的位置
{
if (key == arr[l])
{
return l;
}
}
return -1;
}
}
/// <summary>
/// 索引表：存储主表分块后的每一块信息
/// </summary>
public struct IndexItem
{
public int key;//存放对应块中的最大关键字
public int start;//存放对应块的第一个元素位置
public int end;//存放对应块的最后一个元素位置
}

四、二叉排序树（二叉搜索树）：
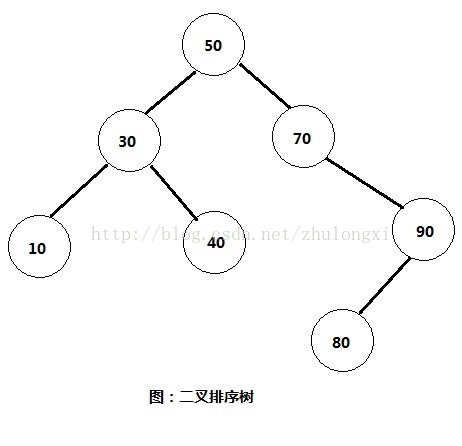
什么是二叉排序树呢？二叉排序树具有以下几个特点。
1，若根节点有左子树，则左子树的所有节点都比根节点小。
2，若根节点有右子树，则右子树的所有节点都比根节点大。
3，根节点的左，右子树也分别为二叉排序树。

下面是二叉排序树常见的操作及思路。

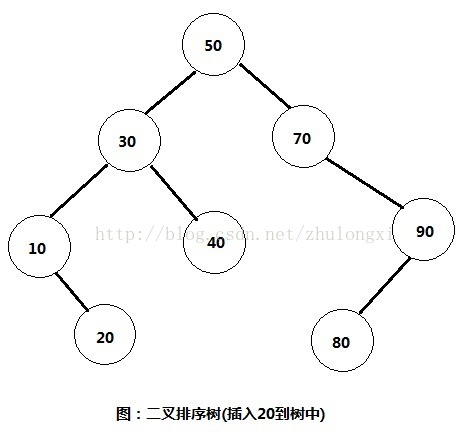
1，插入节点

思路：比如我们要插入数字20到这棵二叉排序树中。那么步骤如下：

1) 首先将20与根节点进行比较，发现比根节点小，所以继续与根节点的左子树30比较。

2) 发现20比30也要小，所以继续与30的左子树10进行比较。

3) 发现20比10要大，所以就将20插入到10的右子树中。

此时二叉排序树效果如图：

2，查找节点

比如我们要查找节点10，那么思路如下：

1) 还是一样，首先将10与根节点50进行比较大小，发现比根节点要小，所以继续与根节点的左子树30进行比较。

2) 发现10比左子树30要小，所以继续与30的左子树10进行比较。

3) 发现两值相等，即查找成功，返回10的位置。

过程与插入相同，这里就不贴图了。

3，删除节点

删除节点的情况相对复杂，主要分以下三种情形：

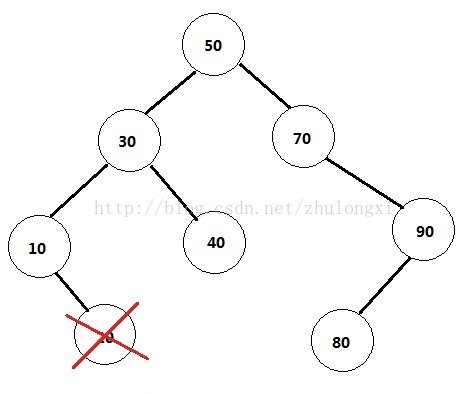
1) 删除的是叶节点(即没有孩子节点的)。比如20，删除它不会破坏原来树的结构，最简单。如图所示。

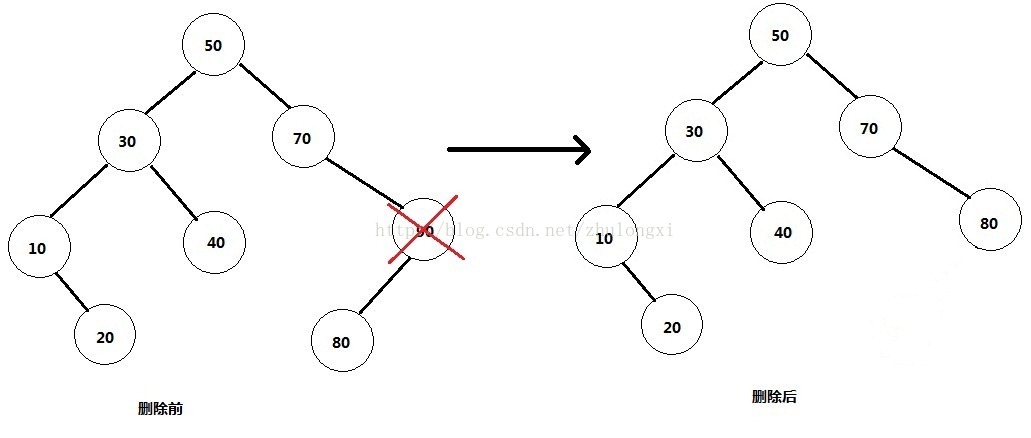
2) 删除的是单孩子节点。比如90，删除它后需要将它的孩子节点与自己的父节点相连。情形比第一种复杂一些。

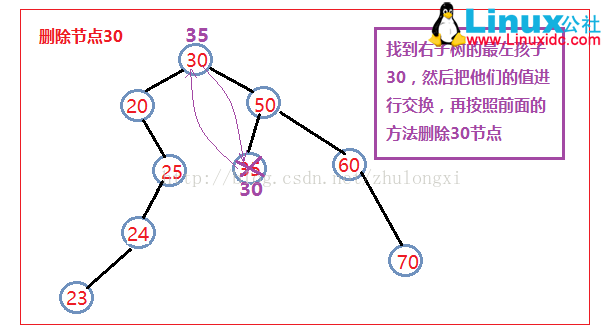
3) 删除的是有左右孩子的节点。

1、找到该节点的右子树中的最左孩子（也就是右子树中序遍历的第一个节点），作为删除节点左右孩子的根结点。
2、把它的值和要删除的节点的值进行交换
3、然后删除这个节点即相当于把我们想删除的节点删除了，返回true；

/// <summary>
/// 创建二叉排序树
/// </summary>
/// <param name="arr"></param>
/// <returns></returns>
public static BSTree CreateBSTree(int[] arr)
{
if (arr == null || arr.Length == 0) return default(BSTree);
BSTree bsTree = new BSTree()
{
Data = arr[0],
Left = null,
Right = null
};
for (int i = 1; i < arr.Length; i++)//0位置已经给根节点了
{
bool isExcute = false;
InsertBSTree(bsTree, arr[i], ref isExcute);
}
return bsTree;
}
/// <summary>
/// 插入节点
/// </summary>
/// <param name="tree"></param>
/// <param name="key"></param>
/// <param name="isExcute"></param>
public static void InsertBSTree(BSTree tree, int key, ref bool isExcute)
{
if (tree == null) return;
if (tree.Data > key)
InsertBSTree(tree.Left, key, ref isExcute);
else
InsertBSTree(tree.Right, key, ref isExcute);
if (!isExcute)
{
BSTree current = new BSTree
{
Data = key,
Left = null,
Right = null
};
if (tree.Data > key) tree.Left = current;
else tree.Right = current;
isExcute = true;
}
}
/// <summary>
/// 中序遍历二叉排序树
/// </summary>
/// <param name="tree"></param>
public static void LDR(BSTree tree)
{
if (tree == null) return;
LDR(tree.Left);
Console.Write(tree.Data + "\t");
LDR(tree.Right);
}
/// <summary>
/// 查找结点
/// </summary>
/// <param name="tree"></param>
/// <param name="key"></param>
/// <returns></returns>
public static bool SearchBSTree(BSTree tree, int key)
{
if (tree == null) return false;
if (tree.Data == key) return true;
if (key < tree.Data) return SearchBSTree(tree.Left, key);
else return SearchBSTree(tree.Right, key);
}
/// <summary>
/// 删除结点
/// </summary>
/// <param name="tree"></param>
/// <param name="key"></param>
public static void DeleteNode(ref BSTree tree, int key)
{
if (tree == null) return;
//判断是否是要删除的节点
if (key == tree.Data)
{
//第一种情况：叶子节点(没有孩子节点)
if (tree.Left == null && tree.Right == null)
{
tree = null;
return;
}
//第二种情况：仅有左子树
if (tree.Left != null && tree.Right == null)
{
tree = tree.Left;
return;
}
//第三种情况：仅有右子树
if (tree.Left == null && tree.Right != null)
{
tree = tree.Right;
return;
}
//第四种情况：有左，右子树
if (tree.Left != null && tree.Right != null)
{
//利用中序遍历找到右节点的左子树的最左孩子
var node = tree.Right;
while (node.Left != null)
{
node = node.Left;
}
node.Left = tree.Left;
//if (node.Right == null)
//{
// DeleteNode(ref tree, node.Data);
// node.Right = tree.Right;
//}
tree = node;
}
}
//遍历找到要删除的节点
if (key < tree.Data) { DeleteNode(ref tree.Left, key); }
else DeleteNode(ref tree.Right, key);
}

/// <summary>
/// 二叉树
/// </summary>
public class BSTree
{
public int Data;
public BSTree Left;
public BSTree Right;
}

五、哈希查找（散列查找）：

根据给定的关键字来计算关键字在表中的地址。

哈希技术是在记录的存储位置和记录的关键字之间建立一个确定的对应关系f，使得每个关键字key对应一个存储位置f(key)。查找时，根据这个确定的对应关系找到给定值的映射f(key),若查找集合中存在这个记录，则必定在f(key)的位置上。哈希技术既是一种存储方法，也是一种查找方法。

六种哈希函数的构造方法：

1，直接定址法：
函数公式：f(key)=a*key+b (a,b为常数)
这种方法的优点是：简单，均匀，不会产生冲突。但是需要事先知道关键字的分布情况，适合查找表较小并且连续的情况。
2，数字分析法：
比如我们的11位手机号码“136XXXX7887”，其中前三位是接入号，一般对应不同运营公司的子品牌，如130是联通如意通，136是移动神州行，153是电信等。中间四们是HLR识别号，表示用户归属地。最后四们才是真正的用户号。
若我们现在要存储某家公司员工登记表，如果用手机号码作为关键字，那么极有可能前7位都是相同的，所以我们选择后面的四们作为哈希地址就是不错的选择。
3，平方取中法：
故名思义，比如关键字是1234，那么它的平方就是1522756，再抽取中间的3位就是227作为哈希地址。
4，折叠法：
折叠法是将关键字从左到右分割成位数相等的几个部分(最后一部分位数不够可以短些)，然后将这几部分叠加求和，并按哈希表表长，取后几位作为哈希地址。
比如我们的关键字是9876543210，哈希表表长三位，我们将它分为四组，987|654|321|0 ，然后将它们叠加求和987+654+321+0=1962，再求后3位即得到哈希地址为962，哈哈，是不是很有意思。
5，除留余数法：
函数公式：f(key)=key mod p (p<=m)m为哈希表表长。
这种方法是最常用的哈希函数构造方法。

6，随机数法：
函数公式：f(key)= random(key)。
这里random是随机函数，当关键字的长度不等是，采用这种方法比较合适。

两种哈希函数冲突解决方法：
我们设计得最好的哈希函数也不可能完全避免冲突，当我们在使用哈希函数后发现两个关键字key1!=key2，但是却有f(key1)=f(key2)，即发生冲突。
方法一：开放定址法：
在开放定址法中，以发生冲突的Hash地址为自变量，通过某种冲突解决函数得到一个新的空闲的Hash地址方法有很多种，一下的是常用的两种：

1.线性探查法：

从发生冲突的地址（设为d）开始，依次探查d的下一个地址（当到达下标为m-1的Hash表表尾时，下一个探查的地址是表首地址0），知道找到一个空位置为止，当m>=n(n是表中的关键字的个数)时一定能找到一个空位置。

线性探查法的公式为：Hi(key)=(H(key)+i) Mod m(1<=i<=m-1)

线性探查法容易产生堆积问题，因为当连续出现若干同义词后，设第一个同义词占用单元d,这连续的若干同义词将占用Hash表的d,d+1,d+2等单元，此时，随后任何d+1，d+2等单元上的Hash映射都会由于前面的同义词堆积而产生冲突，尽管所有这些关键字并没有同义词。

2.平方探查法：

设发生冲突的地址为d，则用平方探查法所得到的新的地址序列为：d+1^2,d-1^,d+2^2,d-2^2,...，平方探查法是一种较好的处理冲突的方法，可以避免出现堆积问题。它的缺点是不能探查到Hash表上的所有单元，但至少能探查到一半的单元。

方法二：链地址法：

链地址法是把所有的同义词用单链表连接起来的方法，在这种方法中，hash表每个单元中存放的不再是记录本身，而是相应同义词单链表的表头指针。

/// <summary>
/// hash表插入
/// </summary>
/// <param name="hastTable"></param>
/// <param name="key"></param>
public static void InsertHashTable(int[] hashTable, int key)
{
int hashAddress = Hash(hashTable, key);
while (hashTable[hashAddress] != 0)
{
hashAddress = (++hashAddress + 1) % hashTable.Length;
}
hashTable[hashAddress] = key;
}
/// <summary>
/// hash查找
/// </summary>
/// <param name="hashTable"></param>
/// <param name="key"></param>
public static int HashSearch(int[] hashTable, int key)
{
int hashAddress = Hash(hashTable, key);
while (hashTable[hashAddress]!=key)
{
hashAddress = (hashAddress + 1) % hashTable.Length;
if (hashTable[hashAddress] == 0 || hashAddress == Hash(hashTable, key)) return -1;
}
return hashAddress;
}
/// <summary>
/// hash函数（除留余数法）
/// </summary>
/// <param name="hashTalbe"></param>
/// <param name="data"></param>
/// <returns></returns>
private static int Hash(int[] hashTalbe, int data)
{
return data % hashTalbe.Length;
}

posted @ 2018-07-04 14:39 lightmare 阅读(453) 评论(0) 编辑收藏举报

刷新页面返回顶部

Lightmare

五大查找

公告