树
摘自《数据结构算法与应用：C++语言描述》第二版 P271
1 树
[软件工程] 考察另一种层次数据——软件工程中的模块化技术。通过模块化，可以把大的复杂的任务分成一组小的不太复杂的任务。模块化的目标是把软件系统分成许多功能不相关的部分或模块以便于进行相对独立的开发。由于解决几个小问题比解决大问题更容易一些，因此模块化方法可以缩短整个软件的开发时间。另外，不同的程序员可以同时开发不同的模块。如果有必要，每个模块可以再细分，从而得到如图 8 - 4所示的用树形表示的模块层次结构。该树给出了某文字处理器的一种可行的模块分解图。
文字处理器的模块层次结构
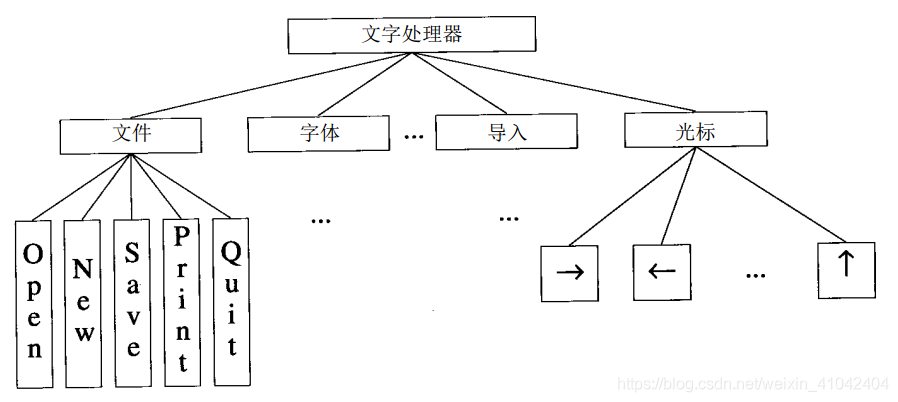
文字处理器的最顶层模块被划分为下一层的几个模块，在图 8 - 4中只给出4个。
文件模块完成与文本文件有关的操作，如打开一个已存在文件（O p e n），打开一个新文件（N e w），保存文件（S a v e），打印文件（P r i n t），从文字处理器中退出（Q u i t）。在层次结构中下一层的每一个模块分别代表一个函数。
字体模块处理与字体有关的所有功能。这些功能包括改变字体、大小、颜色等。若把具有这些功能的模块在图中画出的话，那么它们一定出现在字体模块之下。
导入模块用于处理图形、表格以及其他格式的文本文件。
光标模块处理屏幕上光标的移动。
在接口完全设计好后，程序员可以以相对独立的方式分析、设计和开发每个模块。当一个软件系统以模块化方式划分好之后，可以很自然地以模块为单位来开发该系统。在最终完成的软件系统中，所含有的模块数与模块层次结构中节点数一样多。模块化可以促进对欲解决问题的智能化管理。通过把一个大问题系统地分解成小而相对独立的小问题，可以使大问题的解决更省力。可以将独立的问题分配给不同的人同时解决。而在一个单一模块上进行分工是非常困难的。
开发模块化软件的另一好处是，分开测试一些小而独立的模块比测试一个大的模块要容易得多。层次结构清晰地给出了模块间的关系。
树的另一常用术语为级（l e v e l）。
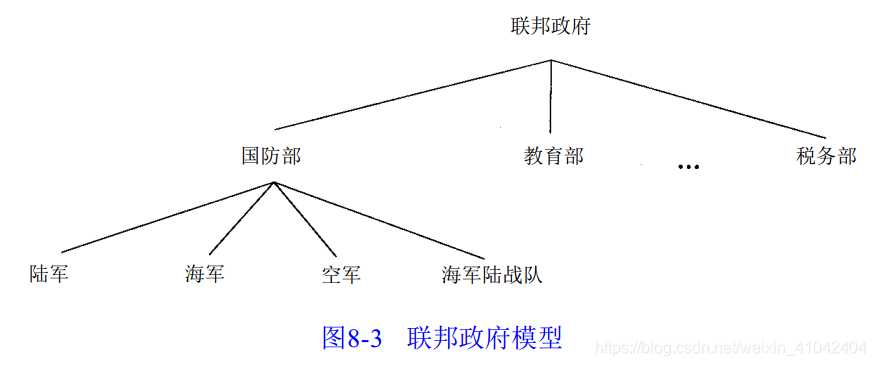
指定树根的级为 1，其孩子（如果有）的级为 2，孩子的孩子为3，等等。在图8 - 3中，联邦政府在第1级，国防部、教育部、税务部在第 2级，陆军、海军、空军和海军陆战队在第3级。
树的高度或深度，是树的级的个数。
元素的度（degree of an element）是指其孩子的个数。叶节点的度为 0，在图8 - 4中文件模块的度为5。
树的度（degree of a tree）是其元素度的最大值。
2 二叉树
2.1 二叉树和树的根本区别
• 二叉树可以为空，但树不能为空。
• 二叉树中每个元素都恰好有两棵子树（其中一个或两个可能为空）。而树中每个元素可有若干子树。
• 在二叉树中每个元素的子树都是有序的，也就是说，可以用左、右子树来区别。而树的子树间是无序的。
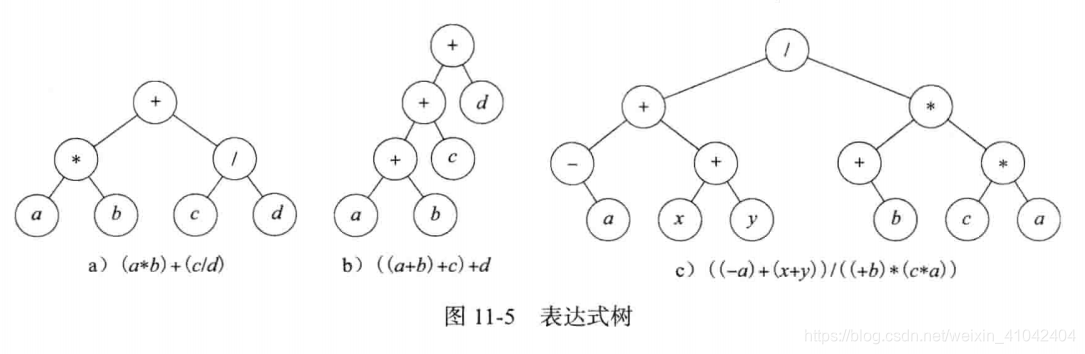
2.2 数学表达式树
每个操作符（十，一， *， /）可以有一个或两个操作数。左操作数是操作符的左子树，右操作数是操作符的右子树。树中的叶节点为常量或变量。
注意在数学表达式树中没有括号。
数学表达式二叉树的一个应用是产生一个表达式的优化代码。
3.二叉树的特性
特性1 含n (n> 0 )个元素的二叉树边数为n-1。
证明 二叉树中每个元素 (除了根节点) 有且只有一个父节点。在子节点与父节点间有且只有一条边，因此边数为n-1。
特性2 若二叉树的高度为h， h≥0，则该二叉树最少有h个元素，最多有( 2^h -1 )个元素。
证明 因为每一层最少要有1个元素，因此元素数最少为h。每元素最多有2个子节点，则第i 层节点元素最多为2^i - 1个， i > 0。 h= 0时，元素的总数为0，也就是2^0 - 1。当h> 0时，元素的总数不会超过( 2^h -1 )。
等比求和：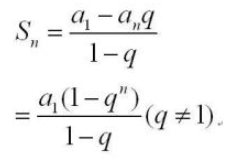
特性3 包含n 个元素的二叉树的高度最大为n，最小为
。
证明 因为每层至少有一个元素，因此高度不会超过 n。由特性2，可以得知高度为h 的二叉树最多有2^h-1个元素。
因为n≤2^h -1，因此h≥l o g2 (n+ 1 )。由于h 是整数，所以h≥。
当高度为h 的二叉树恰好有2^h - 1个元素时，称其为满二叉树（full binary tree）。假设对高度为 h 的满二叉树中的元素按从第上到下，从左到右的顺序从 1到 2^h- 1进行编号（如图8 - 6所示）。
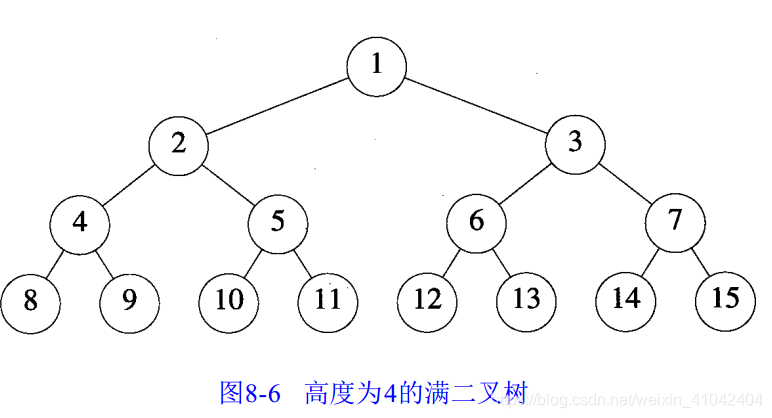
假设从满二叉树中删除 k个元素，其编号为 2^h -i, 1≤i≤k，所得到的二叉树被称为完全二叉树（complete binary tree）。
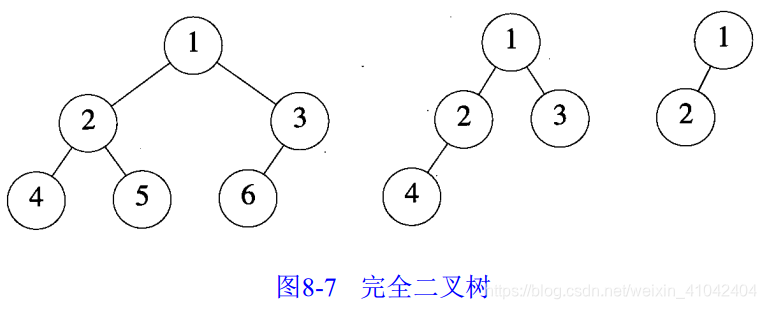
注意满二叉树是完全二叉树的一个特例，并且，注意有 n个元素的完全二叉树的深度为。
在完全二叉树中，一个元素与其孩子的编号有非常好的对应关系。其关系在特性 4中给出。
特性4 设完全二叉树中一元素的序号为i, 1≤i≤n。则有以下关系成立：
1) 当i = 1时，该元素为二叉树的根。若i > 1，则该元素父节点的编号为
。
2) 当2i >n时，该元素无左孩子。否则，其左孩子的编号为 2i。
3) 若2i + 1 >n，该元素无右孩子。否则，其右孩子编号为 2i + 1。
证明 通过对i 进行归纳即可得证。
