Qt绘图（使用QPainter）翻转图像的两种方法

我想要创造一个小人，它可以向四个方向走。我用定时器实现了绘图的循环执行，并从这个图片中把各个帧裁切下来并画出来。

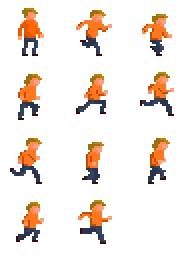
但是，我发现小人的行走动画是向右的。当小人向左走的时候就非常不自然。我想要在这种时候把图像翻转。

于是我尝试着在QPainter中找到一个flip函数——结果居然没有！翻转这样一个非常常用的功能居然没有！

方法一

没有的话，我们就只能自己实现了。我所熟悉的对坐标系进行变形的函数四个：

void shear(qreal sh, qreal sv);
void scale(qreal sx, qreal sy);
void rotate(qreal angle);
void translate(qreal dx, qreal dy)

其中最麻烦的是剪切函数shear。经过探索，它对于右手系的改变相当于乘上一个矩阵：（使用笛卡尔坐标系而不是默认坐标系）

\[\left[ \begin{array}{l} 1 &-sh\\ -sv &1 \end{array} \right] \]

而对于左手系的改变则是：

\[\left[ \begin{array}{l} 1 & sh\\ sv &1 \end{array} \right] \]

这是四个函数中唯一一个可以改变坐标系两个基底的夹角的函数。因为翻转需要我们改变整个坐标系的手性，所以这个函数是必不可少的。

对于放缩函数scale，显然它对坐标系的改变相当于乘上一个矩阵：

\[\left[ \begin{array}{l} sx &0 \\ 0 & sy \end{array} \right] \]

要是sx可以为负数，我的问题其实就已经解决了。但是这个函数不支持负数。

对于旋转函数rotate，它对坐标系的改变相当于乘上一个矩阵：

\[\left[ \begin{array}{l} cos \alpha & -sin \alpha \\ sin \alpha & cos \alpha \end{array} \right] \]

translate的作用是改变原点位置，不是对坐标系进行线性变换，所以与矩阵无关。

于是下面就是数学推导。把初始两个基底向量\((1, 0)\)和\((0, 1)\)变成竖向，放在矩阵里（参考3b1b的线性代数相关视频）：

\[\left[ \begin{array}{l} 1 & 0 \\ 0 & 1 \end{array} \right] \]

不妨进行shear(2, 2)：

\[\left[ \begin{array}{l} 1 & -2\\ -2 & 1 \end{array} \right] \]

此时坐标系就已经变成左手系了。还需要进行一些转换。进行rotate(-90)：

\[\left[ \begin{array}{l} -2 & -1\\ 1 & 2 \end{array} \right] \]

记它为矩阵\(A\)。

我们的目标是水平翻转，所以目标坐标系的两个基底向量是\((-1, 0)\)和\((0, 1)\)。所以现在我们要找到一个矩阵\(X\)，使得\(X \cdot A = \left[\begin{array}{l}-1&0\\0&1\end{array}\right]\)。

求出\(A\)的逆元为：

\[A^{-1}= \left[ \begin{array}{l} -\frac{2}{3} & -\frac{1}{3}\\ \frac{1}{3} & \frac{2}{3} \end{array} \right] \]

所以可得

\[X = \left[\begin{array}{l}-1&0\\0&1\end{array}\right] \cdot A^{-1} = \left[ \begin{array}{l} \frac{2}{3} & \frac{1}{3}\\ \frac{1}{3} & \frac{2}{3} \end{array} \right] = \left[ \begin{array}{l} \frac{2}{3} & 0\\ 0 & \frac{2}{3} \end{array} \right] \cdot \left[ \begin{array}{l} 1 & \frac{1}{2}\\ \frac{1}{2} & 1 \end{array} \right] \]

所以再分别进行一次shear(0.5, 0.5)和scale(2.0/3, 2.0/3)就可以完成翻转了。

综上所述，要在一个以\((cx,cy)\)为左上角的区域内输出一个宽wid的被水平翻转的QPixmap变量frame，使用以下代码：

void drawPixmapFlippedHorizentally(QPainter &qpainter, int cx, int cy, int wid, const QPixmap &frame) {
        qpainter.translate(cx + wid - 1, cy);
        qpainter.shear(2, 2);
        qpainter.rotate(-90);
        qpainter.shear(0.5, 0.5);
        qpainter.scale(2.0/3, 2.0/3);

        qpainter.drawPixmap(QPoint(0, 0), frame);

        qpainter.shear(2, 2);
        qpainter.rotate(-90);
        qpainter.shear(0.5, 0.5);
        qpainter.scale(2.0/3, 2.0/3);
        qpainter.translate(-cx - wid + 1, -cy);
}

打包成一个函数就可以了。真是不容易啊。

方法二

使用QPainter自带的setViewport函数，对展示的坐标系进行转换。

void setViewport(int x, int y, int width, int height)

作用是把画布转换为以\((x,y)\)为原点，\(width\)为宽，\(height\)为高的画布。

原始的画布的原点是\((0,0)\)，宽是\(width()\)，高是\(height()\)（注：这两个函数返回的是窗口的宽和高）。所以，执行函数qpainter.setViewport(0, 0, width(), height())就等于把画布还原到默认状态。

这个函数也能实现坐标系的变换。改变原点位置与矩阵无关，故只有后面的两个参数对坐标系需要纳入考虑。相当于下面这个矩阵：

\[\left[ \begin{array}{l} \frac{width}{width()} & 0\\ 0 & \frac{height}{height()} \end{array} \right] \]

其中\(width\)和\(height\)是函数的参数，而\(width()\)和\(height()\)则是窗口的大小。

所以，只需要以下代码就可以输出一个翻转的图像：

void drawPixmapFlippedHorizentally(QPainter &qpainter, int cx, int cy, int wid, const QPixmap &frame) {
        qpainter.setViewport(cx + wid - 1, cy, -width(), height());
        qpainter.drawPixmap(QPoint(0, 0), frame);
        qpainter.setViewport(0, 0, width(), height())；
}

这是我第一次在生活实践中大量使用线性代数的知识。