蒙提霍尔问题简单粗暴的理解掉
蒙提霍尔问题简单粗暴的理解掉
蒙提霍尔问题,亦称为蒙特霍问题、山羊问题或三门问题,是一个源自博弈论的数学游戏问题,大致出自美国的电视游戏节目Let's Make a Deal。问题的名字来自该节目的主持人蒙蒂·霍尔。与非常类似的有三囚问题。
这个游戏的玩法是:参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车或者是奖品,选中后面有车的那扇门就可以赢得该汽车或奖品,而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,知道门后情形的节目主持人会开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的几率?如果严格按照上述的条件的话,答案是会。换门的话,赢得汽车的几率是2/3。
唔,偶个人用许多的文字理解和阐述是非分困难,换个角度直接从概率和图解的方式来理解更直接简单粗暴嘤嘤嘤,话不多说,上图。
这张图的黄字解释是两个重难点:
1:假设第一次摸到的是羊,那么主持人只能从两只羊中的另一只羊抽取出来展示,那么剩下的另一扇门就必然是汽车了,只要换门就能选上汽车。
0:假设第一次摸到的是汽车,另外两个门里就是两只咩咩了~换门后必然是抽到羊咩咩。

可能还是有些抽象233来看看维基百科介绍的部分
玛丽莲·沃斯·莎凡特在1980年代中期因跻身《吉尼斯世界纪录》中的智商纪录保持人而成名(结果为185)。当时她的答复在《大观杂志》刊出之后引起举世关注。她的解答彻底违反直觉,并引起众多数学家的质疑。但随后的阐释让质疑者颜面无光。显然,莎凡特的答案是正确的-当参赛者转向另一扇门而不是继续维持原先的选择时,赢得汽车的机会将会加倍。
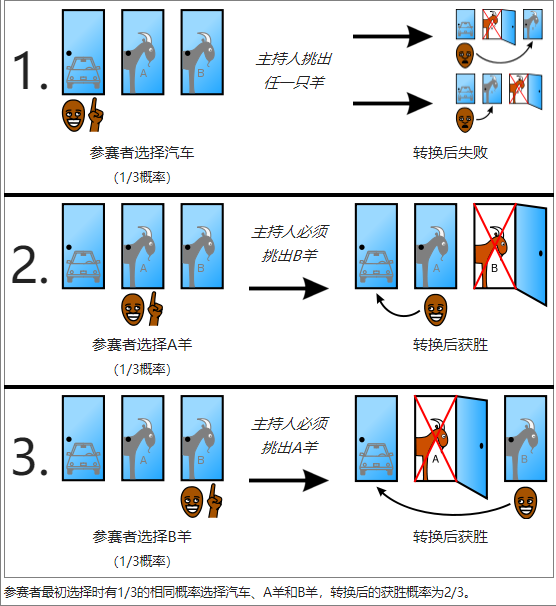
有三种可能的情况,全部都有相等的可能性(1/3):
- 参赛者挑汽车,主持人挑两头羊的任何一头。转换将失败。
- 参赛者挑A羊,主持人挑B羊。转换将赢得汽车。
- 参赛者挑B羊,主持人挑A羊。转换将赢得汽车。
大概就这样吧多多折磨一下概率计算就明白了QAQ文字逻辑自然也就顺了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号