Sculpture (UVa 12171) bfs + 离散化

题意： 某雕塑由 n (n<=50) 个边平行于坐标轴的长方体组成。每个长方体用 6 个整数 x0, y0, z0, x, y, z 表示(1<= x0, y0, z0, x, y, z <= 500)。 x0 为长方体顶点中，x 坐标的最小值，x 表示长方体在 x 方向的长度。其他 4 个值类似定义。统计这个雕像的体积和表面积。注意，雕像内部可能会有密闭的空间，其体积应该算在总体积中。

例样输入：

2
2
1 2 3 3 4 5
6 2 3 3 4 5
7
1 1 1 5 5 1
1 1 10 5 5 1
1 1 2 1 4 8
2 1 2 4 1 8
5 2 2 1 4 8
1 5 2 4 1 8
3 3 4 1 1 1

例样输出：

188 120
250 250

 

解题思路：由于雕塑内部存在密闭空间，不能直接用 bfs 计算雕塑体积。在雕塑周围围上上一圈空气，用广搜遍历空气，体积 = 总体积 - 空气体积，表面积 = 空气与雕塑的接触面积。

注意点：

1、 根据输入数据，需要建立 1000 * 1000 * 1000 的三维坐标系，数据量为 10^9 ，会超内存，因此采用离散化数据的方式。50个长方体最多可能有100 个不同的坐标，因此建立的坐标系为 100 * 100 * 100 的坐标系，数据量为 10^6。

　　离散化： 只关心要用的数据，将大量的或无穷的数据转化成有限个数据，将连续的数据转化成有限个区间，每个区间只存在一种状态。  例如：

　　 

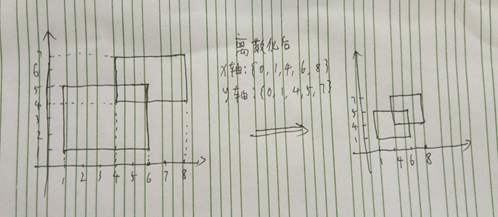
2、 用一个点表示一个长方体。

　　

 

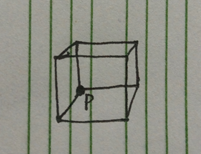
AC代码：

/*  Sculpture (UVa12171) */ 
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;

const int maxn = 105;
const int maxr = 1005;
int dx[] = {1,-1, 0, 0, 0, 0};
int dy[] = {0, 0, 1,-1, 0, 0};
int dz[] = {0, 0, 0, 0, 1,-1};

struct Point{
    int x, y, z;
    Point(int x, int y, int z): x(x), y(y), z(z){}
    Point(){}
};

Point p[maxn];
int x[maxn], y[maxn], z[maxn];        //离散化后的坐标轴
int a[maxn][maxn][maxn];            //离散坐标系
int vis[maxn][maxn][maxn];            //标记是否访问  
int n, nx, ny, nz;                    //数据量以及离散坐标轴的长度
int v, s;

void input();                                    //输入 
void build();                                    //填格子 
void bfs();                                        //广搜求 v 和 s 
int getArea(int tx, int ty, int tz, int dir);    //计算 tx ty tz 长方体在 dir 方向上的面积（与空气的接触面积） 
    
int main(){
    //freopen("input.txt", "r", stdin);
    int T;
    cin >> T;
    while(T--){
        input();
        build();
        bfs();
        cout << s << " " << v << endl;
    }
}

void input(){
    memset(a, 0, sizeof(a));
    memset(vis, 0, sizeof(vis));
    v = 0;    s = 0;
    cin >> n;
    
    for(int i=1; i<=2*n; i+=2){
        cin >> p[i].x    >> p[i].y    >> p[i].z;
        cin >> p[i+1].x    >> p[i+1].y    >> p[i+1].z;
        p[i+1].x += p[i].x;
        p[i+1].y += p[i].y;
        p[i+1].z += p[i].z;        //算出坐标
        
        x[i] = p[i].x;        y[i] = p[i].y;        z[i] = p[i].z;
        x[i+1] = p[i+1].x;    y[i+1] = p[i+1].y;    z[i+1] = p[i+1].z;
    }
    x[0] = 0;             y[0] = 0;              z[0] = 0;
    //将坐标轴排序去重
    sort(x, x+2*n+1);    
    sort(y, y+2*n+1);    
    sort(z, z+2*n+1);
    nx = unique(x, x+2*n+1) - x; 
    ny = unique(y, y+2*n+1) - y;
    nz = unique(z, z+2*n+1) - z;
    //在周围围上空气
    x[nx++] = maxr;        y[ny++] = maxr;     z[nz++] = maxr;
}

void build(){
    for(int i=1; i<=2*n; i++){
        int x1, x2, y1, y2, z1, z2;        //长方体在离散化后的坐标系中的位置
        
        x1 = lower_bound(x, x+nx, p[i].x) - x;
        x2 = lower_bound(x, x+nx, p[i+1].x) - x;
        y1 = lower_bound(y, y+ny, p[i].y) - y;
        y2 = lower_bound(y, y+ny, p[i+1].y) - y;
        z1 = lower_bound(z, z+nz, p[i].z) - z;
        z2 = lower_bound(z, z+nz, p[i+1].z) - z;
        
        for(int i=x1; i<x2; i++)    //左闭右开区间填格子
            for(int j=y1; j<y2; j++)
                for(int k=z1; k<z2; k++)
                    a[i][j][k] = 1; 
    }
}

void bfs(){
    queue<Point> q;
    q.push(Point(0, 0, 0));
    vis[0][0][0] = 1;
    
    while(!q.empty()){
        Point t = q.front();    q.pop();
        //如果这一点为空气，则累加空气体积
        if(a[t.x][t.y][t.z] == 0)
            v += (x[t.x+1] - x[t.x]) * (y[t.y+1] - y[t.y]) * (z[t.z+1] - z[t.z]);
        for(int i=0; i<6; i++){
            int tx, ty, tz;        //与 t 点相邻的点
            tx = t.x + dx[i];
            ty = t.y + dy[i];
            tz = t.z + dz[i];
            if(tx<0 || tx>=nx-1 || ty<0 || ty>=ny-1 || tz<0 || tz>=nz-1)    //过滤掉出界的情况
                continue;
            if(a[tx][ty][tz] == 1){        //为长方体，则计算接触面积并累加
                s += getArea(tx, ty, tz, i); 
            }else if(a[tx][ty][tz] == 0 && vis[tx][ty][tz] == 0){        //为空气并且没访问过，则加入队列 
                q.push(Point(tx, ty, tz));
                vis[tx][ty][tz] = 1;
            }
        }
    }
    
    v = maxr*maxr*maxr - v;
}

int getArea(int tx, int ty, int tz, int dir){
    //不同方向的接触面，面积不同 
    if(dx[dir] != 0){            
        return (y[ty+1]-y[ty]) * (z[tz+1]-z[tz]);
    }else if(dy[dir] != 0){
        return (x[tx+1]-x[tx]) * (z[tz+1]-z[tz]);
    }else{
        return (x[tx+1]-x[tx]) * (y[ty+1]-y[ty]);
    }
}