数值分析第三章 常微分方程的差分方法
常微分方程的差分方法重点回顾:
- 差分方法是一类重要的数值解法,这类方法是要寻求一系列离散结点上的近似解h为步长。一般来说,假定h为定数。
- 能求解的常微分方程的条件。A.两个方程B.满足李普希兹条件C.f(x,y)适当光滑。这样可以保证解存在且唯一。
- 数值解法的第一步是设法消除其导数项,这项手续称“离散化”。由于差分是微分的近似计算,实现离散化的基本途径就是用差商来替代导数。
- 欧拉格式需要熟练掌握。
- 欧拉格式仅为一阶方法(证明是用泰勒公式)
- 隐式欧拉格式也是一阶方法需要掌握
- 两步欧拉格式:调用了前面的两步的信息,是一个二阶方法。
- 梯形格式需要掌握。实质上是欧拉格式和隐式欧拉格式的算术平均。
- 改进的欧拉格式:综合欧拉方法和梯形方法。先用欧拉方法求得一个初步的近似值,即为预报值。然后用它代替梯形方法yn+1进行计算。就得到了预报-校正系统。可以写成嵌套的方式。或者表示为平均化形式
- 龙格库塔方法(背四阶龙格库塔方法)
- 亚当姆预报-校正系统
- 欧拉方法是收敛的
- 欧拉方法是条件稳定的
- 隐式欧拉格式恒稳定(无条件稳定的)
下图是我对教材99页公式的证明
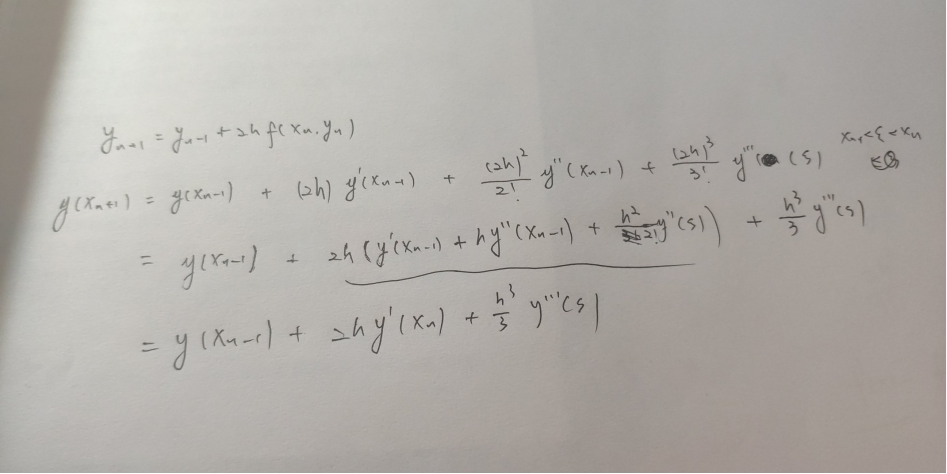
作者:LightAc
出处:https://www.cnblogs.com/lightac/
联系:
Email: dzz@stu.ouc.edu.cn
QQ: 1171613053
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号