现代密码学(对称密码——第一部分)
第三章对称密码(第一部分)
本部分重点:
掌握随机的含义
掌握一次一密的工作原理、实用性不强的原因
掌握流密码的工作原理
掌握完善保密性的含义
掌握语义安全性的含义、安全模型及证明方法
掌握相关定理和推论
一.古典密码->现代密码☆
古典密码
手工或机械方式对字符或单词进行处理
明文一般是有意义的自然语言文本
现代密码
面向计算机和和芯片,对比特、字节或字进行处理
明文可以是任意比特串
二.技术->科学☆
1949年,《保密系统的通信原理》拉开密码学从技术进化到科学的序幕(用信息论研究密码安全性)
三.加密体制的安全性☆
讨论加密体制的安全性时,需要考虑两点:
- 攻击能力:能抵抗攻击者什么类型的攻击
唯密文攻击,已知明文攻击......
- 攻击目的:能阻止攻击者实现什么样的目的
找到密钥,回复特定明文,区分两个明文......
攻击者的攻击能力越强,要实现的目的越低,越难对付。
四.加密体制的分类☆
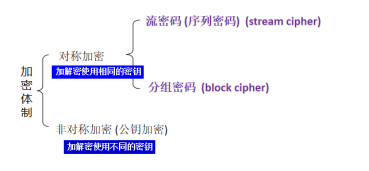
五.对称加密体制的定义☆
定义:对称加密体制是一对高效可计算的算法E和D
E:K × M ->C
D:K × C ->M
满足Dk(Ek(m)) = m, ∀ m ∈ M,k ∈ K
六.随机性☆
随机性的概念在密码学中占有极其重要的地位
随机数不仅可以作为密钥使用
在随机化加密、数字签名等密码体制和协议中也得到广泛应用
七.是否存在真正的随机?☆
是否存在真正的随机性,这是一个哲学问题
量子力学告诉我们:现实世界中存在真随机性
八.随机序列☆
性质:不能可靠重复产生
用完全同样的输入操作两次,得到两个不相关的序列
数学解释:概率服从均匀分布
- 产生每个比特的概率为1/2
- 任意两个比特统计上相互独立
九.如何产生随机序列☆
- 使用一种专门的设备(随机数发生器)
- 输入是不断变化的,输出也就不可重复
- 没人能预测下一个数因为他必须重构输入信号。
十.计算机不能产生真正的随机序列☆
相同计算环境下,对于相同输入,计算机只能产生相同的输出
- 计算机产生的一系列所谓的随机序列是周期性的(周期可以很大)
- 任何周期性的东西都是可以预测的,可预测的就不是随机的
- 要产生真正的随机序列,需要随机的输入,但计算机本身无法提供随机输入
十一.任何人考虑用数学的方法产生随机数肯定是不合理的☆
十二.计算机本身只能产生伪随机序列☆
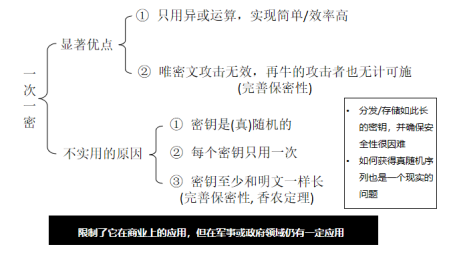
十三.一次一密☆
加解密很简单
加密:明文流与密钥流对应比特异或
解密:密文流与密钥流对应比特异或
密钥流是随机序列,且不重复使用(故得名“一次一密”)
十四.唯密文攻击下密文不能泄露任何信息☆
十五.完善保密性☆
如果一个对称加密体制满足以下条件,则它具有完善保密性
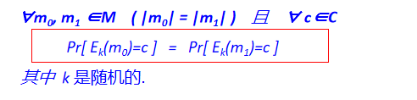
对于任意两个明文,给定密文,攻击者无法确定密文对应哪个明文
及时拥有无限计算资源也无法从密文获得明文的任何信息
唯密文攻击无效
十六.香农定理☆
完善保密性->|K|>=|M|
即使拥有无限计算资源也无法从密文获得明文任何信息(唯密文攻击,无效无条件安全)
密钥至少要和明文一样长(香农定理)
告诉我们:要满足完善保密性,所需密钥至少和明文一样长
给定明文m和其密文c,对应的密钥k有多少个? 1个
十七.一次一密具有完善保密性☆
如何证明加密体制具有完善保密性?
∀ m, c,|k: Ek(m)=c | 是常数,则该加密体制具有完善保密性
不实用!!!
是否可以改造一次一密,让它更实用?
完善保密性->密钥至少要和明文一样长(香农定理)
解决思路:
降低安全性要求->缩短密钥长度
十八.流密码☆
基本思想:
使用“伪随机”密钥流代替“随机”密钥流
使用工具:
“伪随机序列发生器”(PRG)
实现方法:
利用一个短的随机密钥(称作“种子”)作为PRG的输入,由PRG产生伪随机密钥流,再与明文流异或。
十九.PRG☆
G是一个高效可计算的确定性函数,如果G是一个PRG,则
PRG的功能:利用一个短输入 (种子) 产生一个很长的输出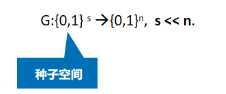
- PRG必须是不可预测的
不可预测性:给定以前输出的某些比特,高效预测下一比特的成功概率可忽略
如果是可预测的,会泄露明文信息
- PRG的安全性:设G是一个PRG,如果对于任何高效的可计算的算法,成功区分G的输出和等长的随机序列的概率都是可忽略的(计算上不可区分),则G是一个安全的PRG
- 一个PRG是安全的->他是不可预测的
- 一个PRG是不可预测的->他是安全的
二十.流密码不具有完善保密性☆
流密码是否能达到完善保密性?
不能,因为密钥比明文短
如何衡量流密码的安全性?
需要换个思路定义“安全” (语义安全性)
总结:完善保密性
- 唯密文攻击无效
- 无条件安全(即使拥有无限计算资源,唯密文攻击也无法破译)
语义安全性:
- 选择明文攻击无效(密钥只用一次)
- 计算上安全(攻击者的计算资源有限,更符合现实)
二十一.语义安全性的定义☆
如果一个对称加密体制是语义安全的,它应满足以下条件是可忽略的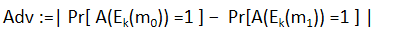
等价于 对于任何高效可计算的攻击者选择的明文m0,m1 { Ek(m0) } ≈c { Ek(m1) }在计算上不可区分
等价的定义
对于任何高效可计算的攻击者选择的明文 m0 , m1 猜中b的优势可以忽略不计
定理:
一次一密是语义安全的
PRG具有不可预测性->相应的流密码是语义安全的
二十二.如果重复使用密钥,流密码不是语义安全的☆
如果重复使用密钥,已知明文攻击下,流密码也很容易被破译
若攻击者获得了一个密文 c 和对应明文 m 时,就很容易得出密钥流。
若重复使用该密钥,就很不安全。
如果重复使用密钥,即使唯密文攻击下,它们仍不安全
好的解决方法
每帧使用一个伪随机密钥
永远不要直接重复使用流密码的密钥!!
网络通信:为每次会话协商一个新密钥
磁盘文件:最好不要用流密码 (修改文件可能泄露文件内容)
二十三.攻击者可能尝试重构生成密钥流的种子☆
攻击原理:
攻击者完全可以知道你收集种子的方法 (柯克霍夫斯原则)
如果你使用的种子不够 “好”,就很容易被攻击者重构。
必须使用“好”的种子,使之具有不可预测性
如何收集种子才是安全的?
毫秒计的时间
用户的输入
鼠标点击的位置,…
它们混合在一起便有了不可预测性,可以抵抗种子猜测攻击

想重复使用密钥时,不要“直接”使用流密码!!!
习题:
随机序列满足 (概率均匀分布) 性质
以下说法正确的是 (攻击目的越容易实现,越难抵抗)
A. 攻击目的越容易实现,越难抵抗
B. 攻击能力越强,越容易抵抗
C. 011100101比10101010随机
D. 以上答案都不对
以下哪种加密体制可以达到完善保密性 ( D )
A. Rabbit B. Salsa20 C. RC4 D. one-time pad
如果一个加密体制达到完善保密性,则 (C )
A. 密钥必须长于明文
B. 密钥可以短于明文
C. 唯密文攻击对它无效
D. 选择明文攻击对它无效


 浙公网安备 33010602011771号
浙公网安备 33010602011771号