Educational Codeforces Round 62 (Rated for Div. 2) 2019年3月23日

Example

Input

9
1 3 3 6 7 6 8 8 9
Output

 1 #include <iostream>
 2 
 3 using namespace std;
 4 
 5 int main () {
 6     int n;
 7     cin >> n;
 8     int a[10010];
 9     for(int i = 0;i < n;i++){
10         cin >> a[i];
11     }
12     int day = 0;
13     int t = 0;
14     for(int i = 1;i <= n;i++){
15         t = max(a[i - 1],t);
16         if(i == t)
17             day++;
18     }
19     cout << day << endl;
20     return 0;
21 }

Example

Input

3
2
<>
3
><<
1
>
Output

1
0
0

 1 // 本题问的是先删除后再按照上述判断 进而看是否能构成
 2 #include <bits/stdc++.h>
 3 
 4 using namespace std;
 5 
 6 int main(){
 7     ios_base::sync_with_stdio(0);
 8     cin.tie(0);
 9     cout.tie(0);
10     int t;
11     cin >> t;
12     while (t--) {
13         int n;
14         cin >> n;
15         string s;
16         cin >> s;
17         int l = 0;
18         int r = n - 1;
19         while(l < n && s[l] == '<')
20             l++;
21         cout << "l :" << l << endl;
22         while(r >= 0 && s[r] == '>')
23             r--;
24         cout << "r " << r << endl;
25         cout << min(l, n - r - 1) << endl;
26         // 从左边开始‘<’的连续个数与从右边开始‘>’的连续个数 两者的最小值即为答案
27         // 因为除去这个边界之后的下一个数一定与它相反 通过它就可以实现转化
28     }
29 }

Examples

Input

4 3
4 7
15 1
3 6
6 8
Output

78
Input

5 3
12 31
112 4
100 100
13 55
55 50

Output
10000

#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+1;
long long n, k, x, y, s, A;
 
pair<int,int>p[N];
 
priority_queue<int>q;
// 优先队列就是大顶堆，队头元素最大
int main(){
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {           // 从第一个开始进行存入
        cin >> x >> y;
        p[i] = make_pair(y, x);
    }
    sort(p + 1, p + n + 1);                     // pair 默认对first升序，当first相同时对second升序（就是对beauty values进行排序）
    for(int i = n; i >= 1; i--) {
        s += p[i].second;               // 将 lengths 从大到小相加
        q.push(-p[i].second);       // 将length的相反数放入队列中
        if (q.size() > k) {              // 当压入的数目超过最大个数时
            s += q.top();                   // s加上最上面压入的元素（正值最小的）
            q.pop();                        // 弹出最上面的
        }                               
        A = max(A, p[i].first * s);         // p[i].first一定是该状态下的最大值
    }
    cout << A << endl;
    return 0;
}

// 一个多变形最多能被分成 n - 2个不重合的三角形
#include <bits/stdc++.h>
 
using namespace std;
 
int main () {
    int n;
    cin >> n;
    int sum = 0;
    for (int i = 2;i < n; i++) {
        sum += i * (i + 1);
    }
    cout << sum << endl;
}

待补！！！

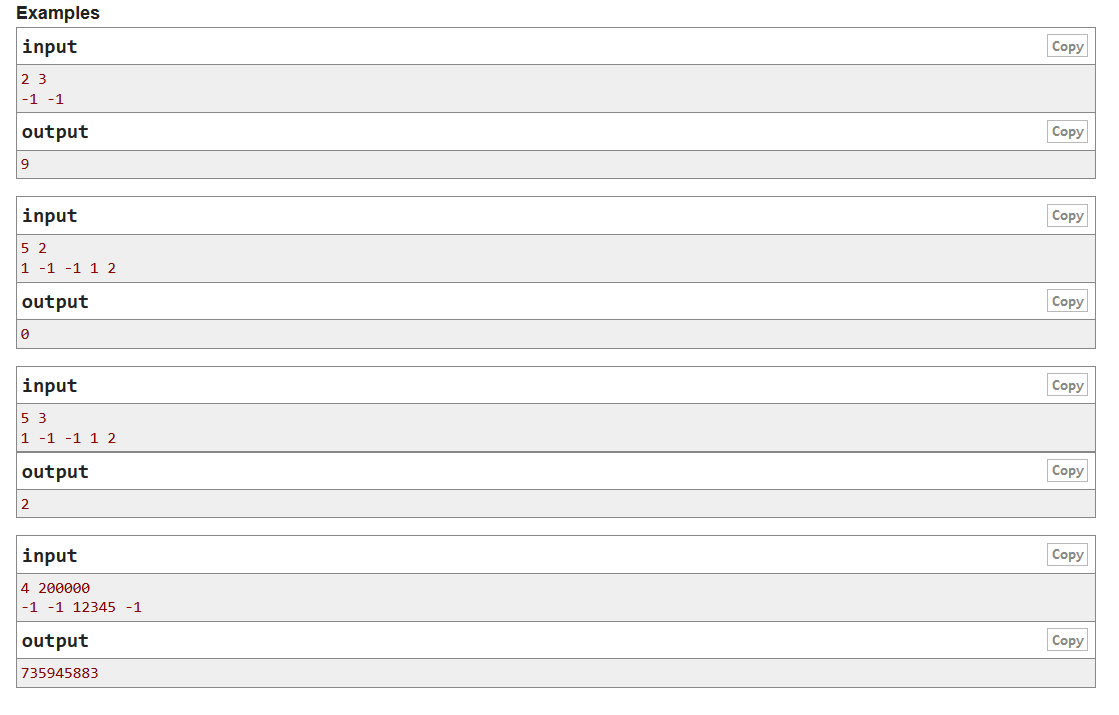
#include <bits/stdc++.h>
 
using namespace std;
 
#define MOD 998244353
 
int n, k, x[2], at;
long long dp[2][2];
int ta;
 
int main() {
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i++) {
        at = i & 1;
        scanf("%d", &ta);
        if (ta == -1) {
            if (x[at] == 0) {
                x[at] = 1;
                dp[at][0] = dp[at][1] = 1;
            } else {
                long long tmp = dp[at][0];
                dp[at][0] = (dp[at][0] * (k - 2) + dp[at][1]) % MOD;
                dp[at][1] = tmp * (k - 1) % MOD;
            }
        } else {
            if (x[at] == 0)
                dp[at][1] = 1;
            else if (ta == x[at])
                dp[at][1] = dp[at][0] * (k - 1) % MOD;
            else
                dp[at][1] = (dp[at][0] * (k - 2) + dp[at][1]) % MOD;
            dp[at][0] = 0;
            x[at] = ta;
        }
    }
    for (int i = 0; i < 2; i++)
        dp[i][0] = (dp[i][0] * (k - 1) + dp[i][1]) % MOD;
    printf("%lld\n", dp[0][0] * dp[1][0] % MOD);
}

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define f(i, x, n) for (int i = x; i < (int)(n); ++i)
 
int const N = 300000;
int q;
vector<pair<int, int> > s[N << 2];
map<pair<int, int>, int> edtm;
vector<pair<int, int> > p;
ll an[N + 1];
 
void adsg(pair<int, int> e, int x, int y, int l = 1, int r = q, int id = 1){
    if (l > y || r < x)return;
    if (l >= x && r <= y) { s[id].push_back(e); return; }
    int m = l + r >> 1, a = id << 1, b = a | 1;
    adsg(e, x, y, l, m, a);
    adsg(e, x, y, m + 1, r, b);
}
 
int pa[N << 1 | 1];
pair<int, int> sz[N << 1 | 1];
stack<pair<int, int> > st;
ll can;
 
int P(int p) { while (pa[p])p = pa[p]; return p; }
void adan(pair<int, int> p) { can += (ll)p.first * p.second; }
void sban(pair<int, int> p) { can -= (ll)p.first * p.second; }
 
void fn(int l = 1, int r = q, int id = 1){
    int undc = 0;
    for (auto &t: s[id]){
        int a = P(t.first), b = P(t.second);
        if (a == b)continue;
        if (sz[a].first + sz[a].second < sz[b].first + sz[b].second)swap(a, b);
        pa[b] = a;
        sban(sz[a]);
        sban(sz[b]);
        sz[a].first += sz[b].first;
        sz[a].second += sz[b].second;
        adan(sz[a]);
        st.push(make_pair(a, b));
        ++undc;
    }
    if (l == r)an[l] += can;
    else {
        int m = l + r >> 1, a = id << 1, b = a | 1;
        fn(l, m, a);
        fn(m + 1, r, b);
    }
    while (undc--){
        int a = st.top().first, b = st.top().second;
        st.pop();
        sban(sz[a]);
        sz[a].first -= sz[b].first;
        sz[a].second -= sz[b].second;
        adan(sz[a]);
        adan(sz[b]);
        pa[b] = 0;
    }
}

100

101

102

103

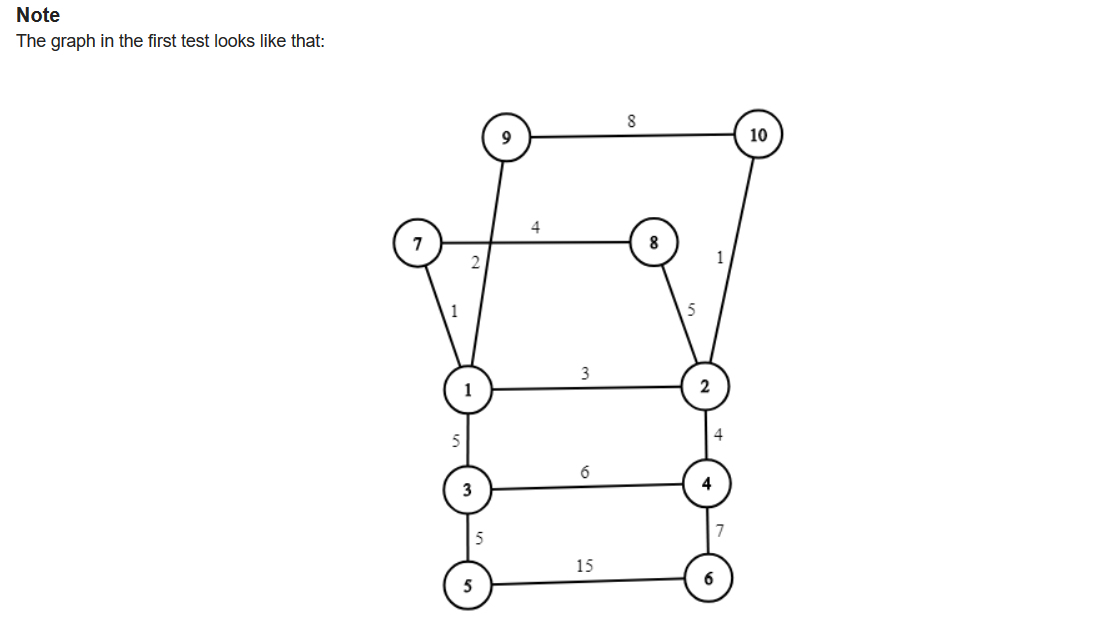
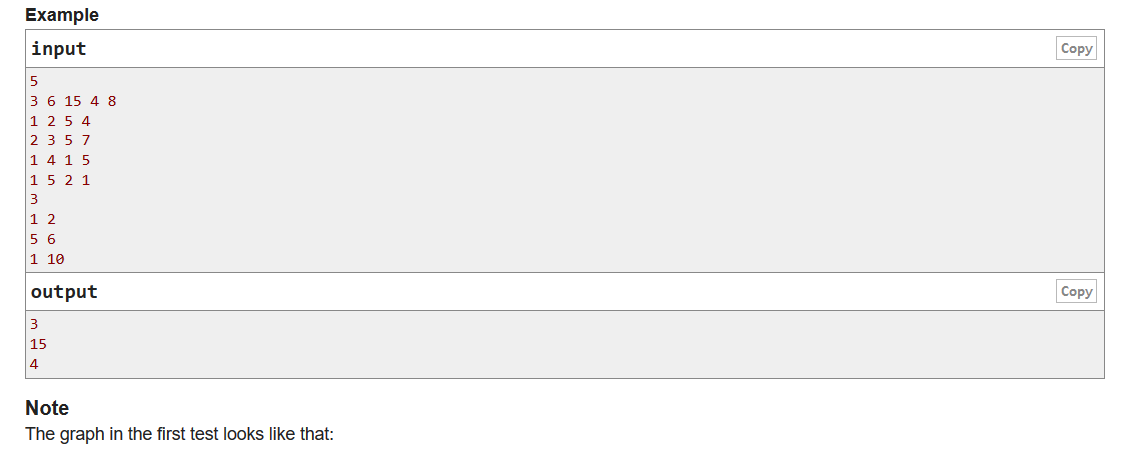
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define f(i, x, n) for (int i = x; i < (int)(n); ++i)
 
ll const inf = 1e18;
int const N = 300000, B = 19;
ll wsd[N + 1], w[N + 1][B][2][2];
int pa[N + 1][B], dp[N + 1];
 
struct E{
    int u;
    ll w[2];
    E(int a, ll b, ll c):u(a) { w[0] = b, w[1] = c; }
};
 
vector<E> tr[N + 1];
 
struct D{
    ll w[2];
    D(int v) { w[0] = w[1] = 0; w[v & 1] = inf; }
    void operator +=(ll c[][2]){
        ll nw0 = min(w[0] + c[0][0], w[1] + c[1][0]);
        w[1] = min(w[0] + c[0][1], w[1] + c[1][1]);
        w[0] = nw0;
    }
};
 
void J(ll a[][2], ll b[][2], ll c[][2]){
    f(i, 0, 2)f(j, 0, 2)c[i][j] = inf;
    f(i, 0, 2)f(j, 0, 2)f(k, 0, 2)c[i][j] = min(c[i][j], a[i][k] + b[k][j]);
}
 
void pl1(int v = 1, int p = 0){
    for (E &t: tr[v])if (t.u != p)pl1(t.u, v);
    for (E &t: tr[v])if (t.u != p)wsd[v] = min(wsd[v], wsd[t.u] + t.w[0] + t.w[1]);
}
 
void pl2(int v = 1, int p = 0) { for (E &t: tr[v])if (t.u != p)wsd[t.u] = min(wsd[t.u], wsd[v] + t.w[0] + t.w[1]), pl2(t.u, v); }
 
void pl3(int v = 1, int p = 0){
    pa[v][0] = p;
    dp[v] = dp[p] + 1;
    int k = 1, z;
    while (k < B && (z = pa[v][k - 1])){
        pa[v][k] = pa[z][k - 1];
        J(w[v][k - 1], w[z][k - 1], w[v][k]);
        ++k;
    }
    for (E &t: tr[v]){
        if (t.u == p)continue;
        w[t.u][0][0][0] = min(t.w[0], t.w[1] + wsd[v] + wsd[t.u]);
        w[t.u][0][0][1] = min(t.w[0] + wsd[v], wsd[t.u] + t.w[1]);
        w[t.u][0][1][0] = min(t.w[1] + wsd[v], wsd[t.u] + t.w[0]);
        w[t.u][0][1][1] = min(t.w[1], t.w[0] + wsd[v] + wsd[t.u]);
        pl3(t.u, v);
    }
}
 
ll wan[2][2];
 
ll go(int a, int b){
    D ca(a), cb(b);
    a = a + 1 >> 1, b = b + 1 >> 1;
    if (dp[a] < dp[b])swap(a, b), swap(cb, ca);
    int d = dp[a] - dp[b], j = 0;
    while (d){
        if (d & 1)ca += w[a][j], a = pa[a][j];
        ++j;
        d >>= 1;
    }
    if (a != b){
        for (int i = B - 1; i >= 0; --i)if (pa[a][i] != pa[b][i])ca += w[a][i], cb += w[b][i], a = pa[a][i], b = pa[b][i];
        ca += w[a][0], cb += w[b][0];
        a = pa[a][0];
    }
    ll an = inf;
    f(i, 0, 2)f(j, 0, 2)an = min(an, ca.w[i] + cb.w[j] + (i != j ? wsd[a] : 0));
    return an;
}
 
int main(){
    int n;
    scanf("%d", &n);
    f(i, 1, n + 1)scanf("%lld", wsd + i);
    f(i, 1, n){
        int a, b;
        ll w1, w2;
        scanf("%d%d%lld%lld", &a, &b, &w1, &w2);
        tr[a].push_back(E(b, w1, w2));
        tr[b].push_back(E(a, w1, w2));
    }
    pl1();
    pl2();
    pl3();
    int q;
    scanf("%d", &q);
    while (q--){
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%lld\n", go(a, b));
    }
}