2021杭电多校第一场
【Maximal submatrix】
题面:给出一个N * M矩阵,求出最大的列上升子矩阵
1.矩阵处理
for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(mp[i][j] >= mp[i-1][j]) mp1[i][j] = mp1[i-1][j] + 1; else mp1[i][j] = 1; } }
接下来问题转换为 对该矩阵求最大的子矩阵大小
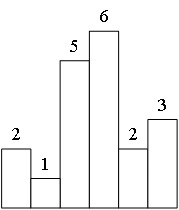
如上图,我们可以把每一行的数字考虑为一个高为mp1[i][j]的方块,利用单调栈分别求解每一行的最大子矩形面积复杂度为O(N * M)

#include <iostream> #include <stdio.h> #include <string.h> #include <stack> #include <queue> #include <map> #include <set> #include <vector> #include <math.h> #include <bitset> #include <algorithm> #include <climits> #include<functional> #include<time.h> #include<stdlib.h> #include<sstream> #include <iomanip> #include<list> #include "assert.h" using namespace std; #define Pair pair<int, int> #define ULL unsigned long long #define LS l,mid,lson #define RS mid+1,r,rson #define MEM(a,x) memset(a,x,sizeof(a)) #define gcd(a,b) __gcd(a,b) #define ll long long #define esp 1e-8 #define lowbit(x) (x&-x) #define girlfriend zy #define E exp(1.0) #define PI acos(-1.0) //#define int long long #define pb(x) push_back(x) #define debug(x) cout<<#x<<" "<<x<<endl; #define rtf return false; #define rtt return true; // lower_bound(a.begin(),a.end(),tmp,greater<ll>()) 第一个小于等于的 void puty(){puts("YES");} void putn(){puts("NO");} const int maxn = 4e5 + 10; const int MOD = 1e9 + 7; const int mod = 998244353; const int INF = 0x3f3f3f3f; ///1 061 109 567 const int maxx = 1e7 + 10; int mp[2020][2020]; int mp1[2020][2020]; int n,m; struct node { int val,cnt; }; node x[2020]; int getarea(int a[]) { int ans = 0; for(int i = 1 ;i <= m;i++) { x[i].val = a[i]; x[i].cnt = i; } stack<node> st; x[m+1].val = 0; st.push(x[1]); for(int i=1;i<=m+1;i++) { if(x[i].val > st.top().val) st.push(x[i]); else { int left = 0; while(!st.empty() && x[i].val <= st.top().val) { node j; j = st.top(); st.pop(); ans = max(ans,(i - j.cnt) * j.val); left = j.cnt; } x[i].cnt = left; st.push(x[i]); } } return ans; } int main() { int t; scanf("%d",&t); while(t--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { scanf("%d",&mp[i][j]); } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(mp[i][j] >= mp[i-1][j]) mp1[i][j] = mp1[i-1][j] + 1; else mp1[i][j] = 1; } } int ans = 0; for(int i=1;i<=n;i++) { ans = max(ans,getarea(mp1[i])); } printf("%d\n",ans); } }
【Xor sum】
题面:给出n个数,找到最短的区间异或和大于等于K 若没有则输出" - 1 "
思路:01字典树处理区间异或最大值,同时更新区间长度和左右端点
(1)区间异或处理:处理整个数组的前缀异或和(每个前缀和的值与整个字典树查找最大值与K的关系) 操作完成之后再将这个值插入字典树
————原理(假设当前枚举到的前缀和在数组中的位置为R 众所周知a[r] ^ a[l] = a[l —> r -1]的异或和 )
由X xor X = 0 ; 0 xor Y = Y;所有【l,r】 = 【1,r】 XOR 【1,l - 1】
这样在一颗加入了r 前的所有前缀异或和的01字典树上查找【1,r】就能得到以r为右边界的最大异或和
(2)然后你需要一个Cnt数组 记录 当前这个节点的值 在数组中最靠右边的位置 因为你要区间最小(好好理解)

#include <iostream> #include <stdio.h> #include <string.h> #include <stack> #include <queue> #include <map> #include <set> #include <vector> #include <math.h> #include <bitset> #include <algorithm> #include <climits> #include<functional> #include<time.h> #include<stdlib.h> #include<sstream> #include <iomanip> #include<list> #include "assert.h" using namespace std; #define Pair pair<int, int> #define ULL unsigned long long #define LS l,mid,lson #define RS mid+1,r,rson #define MEM(a,x) memset(a,x,sizeof(a)) #define gcd(a,b) __gcd(a,b) #define ll long long #define esp 1e-8 #define lowbit(x) (x&-x) #define girlfriend zy #define E exp(1.0) #define PI acos(-1.0) //#define int long long #define pb(x) push_back(x) #define debug(x) cout<<#x<<" "<<x<<endl; #define rtf return false; #define rtt return true; // lower_bound(a.begin(),a.end(),tmp,greater<ll>()) 第一个小于等于的 void puty(){puts("YES");} void putn(){puts("NO");} const int maxn = 1e7 + 10; const int MOD = 1e9 + 7; const int mod = 998244353; const int INF = 0x3f3f3f3f; ///1 061 109 567 int tree[maxn][2]; int a[maxn]; int cnt[maxn]; int tot = 0; int k; void insert(int x,int pos) { int s = 0,tmp; for(int i=31;i>=0;i--) { tmp = x >> i & 1; if(!tree[s][tmp]) tree[s][tmp] = ++tot; s = tree[s][tmp]; cnt[s] = max(cnt[s],pos); } } int get(int x) { int s = 0,tmpk,tmpx; int l = 0; for(int i=31;i>=0;i--) { tmpx = x >> i & 1; tmpk = k >> i & 1; if(!tmpx) { if(!tmpk) { l = max(l,cnt[tree[s][1]]); if(!tree[s][0]) return l; s = tree[s][0]; } else { if(!tree[s][1]) return l; s = tree[s][1]; } } else { if(!tmpk) { l = max(l,cnt[tree[s][0]]); if(!tree[s][1]) return l; s = tree[s][1]; } else { if(!tree[s][0]) return l; s = tree[s][0]; } } } return l = max(l,cnt[s]); } int main() { int t; scanf("%d",&t); while(t--) { int n; scanf("%d%d",&n,&k); for(int i=0;i<=tot;i++) { tree[i][0] = tree[i][1] = 0; cnt[i] = 0; } tot = 0; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); a[i] ^= a[i-1]; } int ans = INF; int ansl = 0,ansr = 0; insert(0,0); for(int i=1;i<=n;i++) { int l = get(a[i]); if(l && i - l < ans) { ans = i - l; ansl = l + 1; ansr = i; } insert(a[i],i); } if(ans != INF) { printf("%d %d\n",ansl,ansr); } else { printf("-1\n"); } } }
【KD-Graph】
思路:按边从小到大排序,维护连通块数量 等于K时 答案 = e[i-1].val 然后跟 e[i].val比较 如果相等 输出 “-1" 不相等输出e[i-1].val

#include <iostream> #include <stdio.h> #include <string.h> #include <stack> #include <queue> #include <map> #include <set> #include <vector> #include <math.h> #include <bitset> #include <algorithm> #include <climits> #include<functional> #include<time.h> #include<stdlib.h> #include<sstream> #include <iomanip> #include<list> #include "assert.h" using namespace std; #define Pair pair<int, int> #define ULL unsigned long long #define LS l,mid,lson #define RS mid+1,r,rson #define MEM(a,x) memset(a,x,sizeof(a)) #define gcd(a,b) __gcd(a,b) #define ll long long #define esp 1e-8 #define lowbit(x) (x&-x) #define girlfriend zy #define E exp(1.0) #define PI acos(-1.0) //#define int long long #define pb(x) push_back(x) #define debug(x) cout<<#x<<" "<<x<<endl; #define rtf return false; #define rtt return true; // lower_bound(a.begin(),a.end(),tmp,greater<ll>()) 第一个小于等于的 void puty(){puts("YES");} void putn(){puts("NO");} const int maxn = 1e7 + 10; const int MOD = 1e9 + 7; const int mod = 998244353; const int INF = 0x3f3f3f3f; ///1 061 109 567 struct node { int from,to,val; node(int u,int v,int w) { from = u,to = v,val = w; } node(){}; }e[maxn]; int head[maxn]; int pre[maxn]; int find(int x) { if(x == pre[x]) return x; return pre[x] = find(pre[x]); } void uoin(int x,int y) { int fx = find(x); int fy = find(y); if(fx == fy) return; pre[fx] = fy; } int cmp(node a,node b) { return a.val < b.val; } int main() { // freopen("1.in","r",stdin); //freopen("1.out","w",stdout); int t; scanf("%d",&t); while(t--) { int n,m,k; scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;i++) { head[i] = -1; pre[i] = i; } for(int i=1;i<=m;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); e[i] = {node{u,v,w}}; } sort(e+1,e+1+m,cmp); int ans = 0; int comp = 0; int tot = n; for(int i=1;i<=m;i++) { int fx = find(e[i].from); int fy = find(e[i].to); if(tot == k) { ans = e[i-1].val; comp = e[i].val; } if(fx != fy) { uoin(fx,fy); tot--; } } if(comp == ans) { printf("-1\n"); } else { printf("%d\n",ans); } } }
【zoto】
思路:莫队按x轴分块维护每一个块的区间,然后用树状数组维护(线段树T了 Orz)对跟Y轴平行方向上的点的个数

#include <iostream> #include <stdio.h> #include <string.h> #include <stack> #include <queue> #include <map> #include <set> #include <vector> #include <math.h> #include <bitset> #include <algorithm> #include <climits> #include<functional> #include<time.h> #include<stdlib.h> using namespace std; #define Pair pair<int, int> #define ULL unsigned long long #define LS l,mid,lson #define RS mid+1,r,rson #define MEM(a,x) memset(a,x,sizeof(a)) #define gcd(a,b) __gcd(a,b) #define ll long long #define N 10 #define EXP 1e-8 #define lowbit(x) (x&-x) #define girlfriend zy #define E exp(1.0) #define PI acos(-1.0) //#define int long long #define pb(x) push_back(x) #define debug(x) cout<<#x<<" "<<x<<endl; void puty(){puts("YES");} void putn(){puts("NO");} const int maxn = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; int fx[100010],b[100010]; int vis[100010],ans[100010],fen[100010]; void modify(int x,int k) { for(int i=x; i<100010; i+=lowbit(i)) b[i]+=k; } int get(int x) { int ans = 0; for(int i=x; i; i-=lowbit(i)){ ans+=b[i]; } return ans; } int query(int x,int y) { return get(y)-get(x-1); } struct sut{ int id,lx,ly,rx,ry; }a[100010]; bool cmp(sut m,sut n){ return fen[m.lx]==fen[n.lx]?m.rx<n.rx:fen[m.lx]<fen[n.lx]; } void add(int x){ if(!vis[fx[x]]){ modify(fx[x],1); } vis[fx[x]]++; } void delet(int x){ if(vis[fx[x]]==1){ modify(fx[x],-1); } vis[fx[x]]--; } int main(){ ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); int t; cin>>t; while(t--) { memset(vis,0,sizeof vis); memset(b,0,sizeof(b)); int n,m; cin>>n>>m; for(int i=1;i<=n;i++){ cin>>fx[i]; fx[i]++; fen[i]=(i -1 )/ sqrt(n) + 1; } for(int i=1;i<=m;i++){ int lx,ly,rx,ry; cin>>lx>>ly>>rx>>ry; ly++; ry++; a[i]={i,lx,ly,rx,ry}; } sort(a+1,a+1+m,cmp); int xl=1,xr=0; for(int i=1;i<=m;i++){ while(a[i].lx<xl){ add(--xl); } while(a[i].rx>xr){ add(++xr); } while(a[i].lx>xl){ delet(xl++); } while(a[i].rx<xr){ delet(xr--); } ans[a[i].id]=query(a[i].ly,a[i].ry); } for(int i=1;i<=m;i++){ cout<<ans[i]<<endl; } } return 0; }



