倍增优化DP Codeforces 1175E

9:38am;

初步设想：线段树覆盖

 

 

 

从根节点开始 对已给区间进行染色 如果查询区间 有未被染色部分 则输出 -1

 

10:24am;

但我寻思着？咋统计最小个数？

 

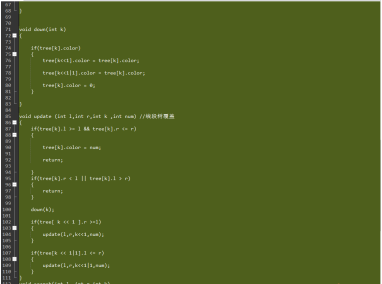
CTRL + A

 

 

 

 

10:40

灵光乍现

 

 

从查询的左节点依次开始往后覆盖，如果后面节点的长度 > 查询节点节点覆盖的最长 长度 那我ans++；

 

那就不需要线段树存状态了，依次查询就行了。

 

11:00am

 

一直在存状态，但是需要一输入就进行处理，（自闭一会，不会写了）

 

 

好家伙写了一半 又觉得像线段树了。查询这个区间是否覆盖。

 

 

好家伙线段树写了一半觉得这个又处理不了

（自闭了）

 

 

 

 

 

 

 

 

 

然后面对CSDN编程

 

 

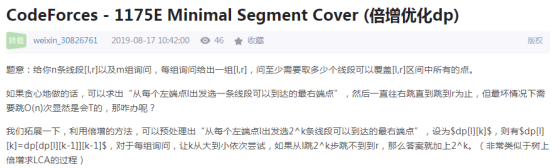
什么？不是线段树 那没事了

 

 

哦 是DP那没事了

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

我：

 

 

 

 

 

好家伙 （明白了 这就去写线段树）

 

 

 

 

 

12:32

 

啥都不会

 

这就去请教 数据结构 大佬

 

 

 

 

 

 

开始自闭学习 倍增优化DP

 

14:40

 

（1）为什么这道题要使用倍增

 

（2）倍增的基本思想

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

第一点：

 

给你n条线段[l,r]以及m组询问，每组询问给出一组[l,r]，问至少需要取多少个线段可以覆盖[l,r]区间中所有的点。

如果贪心地做的话，可以求出“从每个左端点l出发选一条线段可以到达的最右端点”，然后一直往右跳直到跳到r为止，

 

 

 

 

 

 

 

这种复杂度是o(n)的，然后满心欢喜的写上去 你最终发现

 

 

 

 

 

 

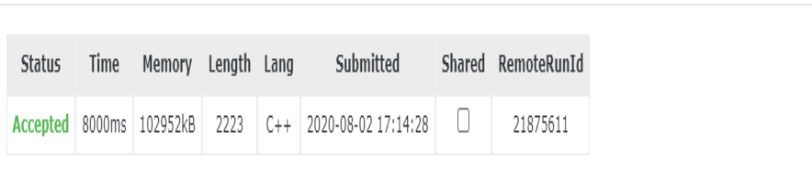
然后你就会

以8000ms的时间通过这道题（雾

我开玩笑的

 

 

你就会

 

 

 

 

 

引入倍增这个思想

 原博客地址 ：https://blog.csdn.net/dong_qian/article/details/81702697

15：22

 

 

 

 

这个兔子想从A ————> B

 

有一个2B小白兔，左右反复横跳

 

有一个普通小白兔 一步一步的往B跳

 

有一个超级小白兔 就直接飞一步到位

 

啊这时候就有人问了，这超级小兔子怎么一步到位呢？

 

那当然是前一天晚上 他先学普通小兔子一步一步跳，然后拿上宋毅学姐发给他的小抄本 记录下了这个位置

第二天直接一步飞过去

 

但是如果小白兔的目的地多了，宋毅学姐送他的小抄本就不够用

这个时候怎么办呢

他就需要宋毅学姐继续送他小抄本，但是宋毅学姐很忙，他又没钱自己买小抄本

 

所以他请教了王永琪大佬，想问问他有什么新的打小抄方式

 

 

 

 

 

 

 

 

 

 

他告诉小白兔

从A出发跳1步到1（记到小本本上）

从1出发跳1步到2（记到小本本上）

跳一步的就记录完了

 

 从A出发跳2步？就是从A出发跳1步再跳1步的到的地方，翻看小抄，直接誊写从1出发跳1步会到的2这个格子作为A跳2步会到的格子。

从1出发跳2步？跟刚才一样，直接誊写。

（跳2步的记录完毕）

 

从A出发跳4步？不会真去跳4步吧？不，它也就是等于从A出发跳2步到的2号点再跳2步会到的格子，那么我们直接誊写2号格子跳2步会到的格子就可以了。

 

 

 

 

 

 

 

然后

 

利用倍增的方法，可以预处理出

从每个左端点l出发选2^k条线段可以到达的最右端点，设为dp[l][k]，

 

则有

dp[l][k]=dp[dp[l][k−1]][k−1]dp[l][k]=dp[dp[l][k−1]][k−1]，

 

 

对于每组询问，让k从大到小依次尝试，如果从l跳2^k步跳不到r，那么答案就加上2^k。

 

16:12分 题目A了