Adaboost：原理及python实现
Table of Contents
Adaboost概述
Boosting提升方法是集成学习的另一种策略。
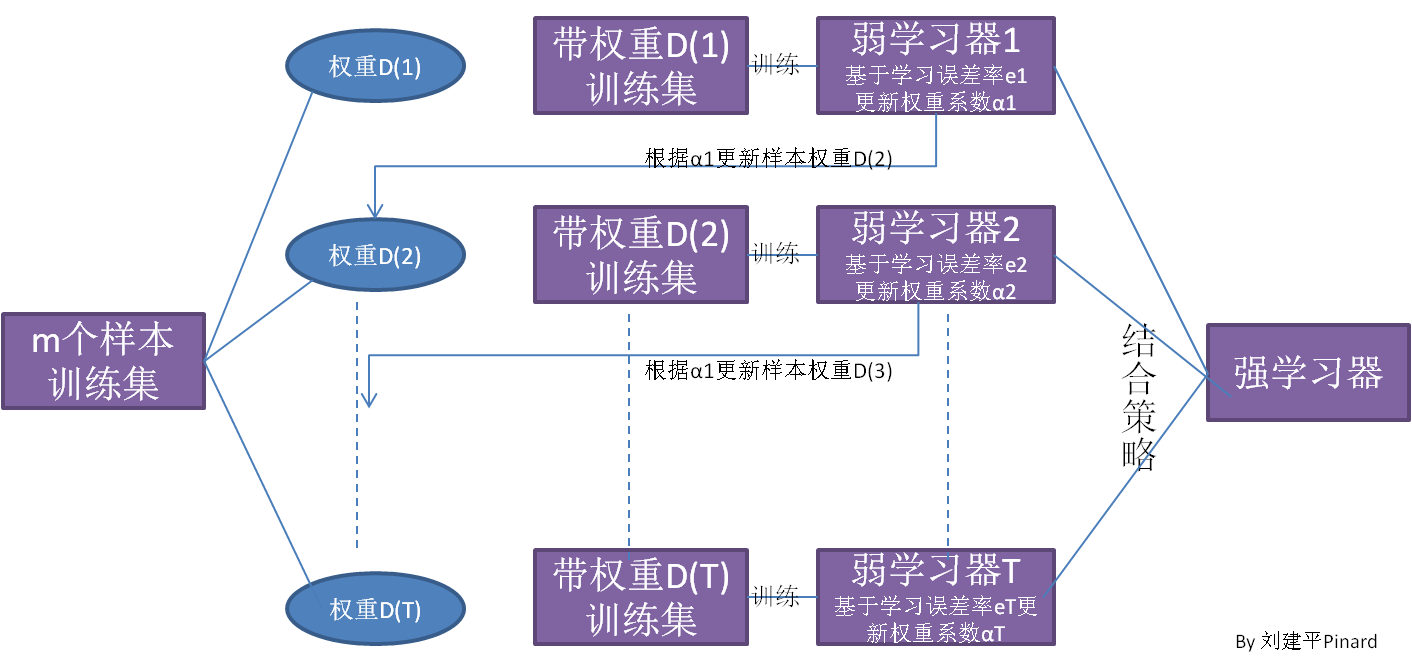
Adaboost的整体流程如上图所示。首先，训练一个弱学习器，其样本权重是相同的，根据训练结果，对样本的权重重新赋值，对于分类错误的样本提高其样本权重，然后使用更新后的样本训练第二个学习器，一直重复直到结束。最后，使用结合策略将几个弱学习器结合起来，形成最终的模型
Adaboost的核心思想就是，对于错误样本，赋予更高的权重，使模型更关注错误样本。对于错误率高的学习器，结合时候，给与更低的权重，使更准确的学习器有更多的话语权。
分类
算法流程
上一节大致讲了Adaboost的算法思路，但是有几个问题需要详细解决：
- 如何获取更新权重系数\(\alpha\)来更新样本权重
- 使用什么方法获得强学习器
Adaboost算法
输入：训练集\(T=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m),y\in\{1,-1\}\)
输出：最终分类器\(G（x）\)
- 初始化样本权重
\[D_1=（w_{11},w_{12},...,w_{1m}）,w_{1i}=\frac1m
\]
- 对于\(k = 1,2,3,...,K\)
- 使用权重系数为\(D_k\)的样本集学习，获得弱分类器\(G_k(x)\)
- 计算分类器错误率e
\[e_k =\sum_{i=1}^{m}w_{ki}I(G_k(x_i)\neq y_i)
\]
其中
\[I(G_k(x_i)\neq y_i)=\left\{
\begin{aligned}
1, G_k(x_i)\neq y_i\\
0, G_k(x_i)= y_i\\
\end{aligned}
\right.\]
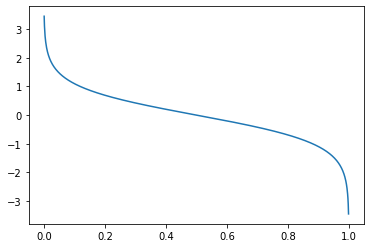
- 计算分类器权重\(\alpha_k\)
\[\alpha_k = \frac12log\frac{1-e_k}{e_k}
\]
这个权重函数的图像如下所示，随着错误率增加，权重不断降低。当分类错误率为50%，也就是说这个分类器是随机分类时，该分类器的权重就是0。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
x = np.linspace(0,1,1000,endpoint=False)
y = 0.5 * np.log((1-x)/x)
plt.plot(x,y)
plt.show()
- 计算下一轮样本权重
\[D_{k+1}=(w_{k+1,1},w_{k+1,2},...,w_{k+1,m})
\]
\[w_{k+1,i} = \frac{w_{ki}}{Z_k}e^{-\alpha_ky_iG_k(x_i)}
\]
或者也可以写为
\[w_{k+1,i} = \left\{\begin{aligned}
\frac{w_{ki}}{Z_k}e^{-\alpha_k},G_k(x_i)=y_i\\
\frac{w_{ki}}{Z_k}e^{\alpha_k},G_k(x_i)\neq y_i
\end{aligned}\right.\]
其中
\[Z_k = \sum_{i=1}^m w_{ki}e^{-\alpha_ky_iG_k(x_i)}
\]
可以看出，每次跟新权重后，权重和仍然为1，由于通常情况下，\(\alpha_k>0\)，所以，当分类错误时，样本的权重增加。
- 构建基分类器的组合
\[f(x)=\sum_{k=1}^{K}\alpha_kG_k(x)
\]
得到最终分类器
\[G(x) = sign(f(x))
\]
Adaboost的前向分步算法解释
Adaboost使用加法模型
\[f(x)=\sum_{k=1}^{K}\alpha_kG_k(x)
\]
优化问题可表示为
\[min \sum_{i=1}^mL(y_i,f(x_i))
\]
通常这是一个复杂的优化算法，前向分步算法的思想是：对于加法模型，每次只优化一个基分类器，然后逐步逼近目标函数。具体的，每次只优化以下函数：
\[min \sum_{i=1}^mL(y_i,\alpha_kG_k(x_i))
\]
Adaboost使用指数损失函数：
\[L = \sum_{i=1}^me^{-y_if(x_i)}
\]
第k轮的优化就是
\[L = \sum_{i=1}^me^{-y_if_k(x_i)}=\sum_{i=1}^me^{-y_i[f_{k-1}（x_i）+\alpha_kG_k(x_i)]}= \sum_{i=1}^mw_{ki}e^{-\alpha_ky_iG_k(x_i)}
\]
显然,使用的基分类器\(G_k(x)\)是错误率最低的分类器即为最优，因此，只需要优化分类器权重\(\alpha_k\)。同上，损失函数可以拆分为\(G_k(x)\)为{1，-1}的两部分：
\[L = \sum_{y_i=G_k(x_i)}w_{ki}e^{-\alpha_k}+\sum_{y_i\neq G_k(x_i)}w_{ki}e^{\alpha_k}
\]
由于
\[\sum_{y_i\neq G_k(x_i)}w_{ki}e^{\alpha_k}=e^{\alpha_k}\sum_{i=1}^mw_{ki}I(y_i\neq G_k(x_i))
\]
\[\sum_{y_i=G_k(x_i)}w_{ki}e^{-\alpha_k}=e^{-\alpha_k}\sum_{i=1}^mw_{ki}-e^{-\alpha_k}\sum_{i=1}^mw_{ki}I(y_i\neq G_k(x_i))
\]
故
\[L = (e^{\alpha_k}-e^{-\alpha_k})\sum_{i=1}^mw_{ki}I(y_i\neq G_k(x_i))+e^{-\alpha_k}\sum_{i=1}^mw_{ki}
\]
\[\frac{\partial L}{\partial \alpha_k}=(e^{\alpha_k}+e^{-\alpha_k})\sum_{i=1}^mw_{ki}I(y_i\neq G_k(x_i))-e^{-\alpha_k}\sum_{i=1}^mw_{ki}=0
\]
将错误率
\[e_k = \frac{\sum_{i=1}^mw_{ki}I(y_i\neq G_k(x_i))}{\sum_{i=1}^mw_{ki}}
\]
代入上式得
\[(e^{2\alpha_k}+1)e_k-1=0
\]
\[\alpha_k=\frac12ln(\frac 1{e_k}-1)
\]
对于权重
\[w_{ki}=e^{-y_if_{k-1}（x_i）}=w_{k-1,i}e^{-y_i\alpha_{k-1}\space G_{k-1}\space\space(x_i)}
\]
跟前面得更新权重只差了一个\(Z_{k-1}\)，对于每一轮更新\(Z_{k-1}\)是常数，因此是等价的。
python实现
这里使用sklearn的DecisionTreeClassifier为基模型，实现了Adaboost算法，可以看出，与Sklearn实现准确率相近。
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_classification
from sklearn.ensemble import AdaBoostClassifier as ADASklern
class AdaboostClassifier:
def __init__(self, X, y, n_estimator=100):
self.X = np.array(X)
self.y = np.array(y).reshape(-1, 1)
self.y[self.y == 0] = -1
self.n_estimator = n_estimator
self.estimators = []
self.estimator_weights = np.ones(self.n_estimator)
self.estimator_errors = np.zeros(self.n_estimator)
self.sample_weights = np.ones(self.X.shape[0]) / self.X.shape[0]
def fit(self):
for i_estimator in range(self.n_estimator):
base_estimator = DecisionTreeClassifier(max_depth=1).fit(
self.X, self.y, self.sample_weights)
self.estimators.append(base_estimator)
y_pre = base_estimator.predict(self.X)
error_rate = sum(self.sample_weights * \
(np.ravel(y_pre) != np.ravel(self.y)).astype(int)) / self.sample_weights.sum()
estimator_weight = 0.5 * np.log((1 - error_rate) / error_rate)
self.estimator_errors[i_estimator] = error_rate
self.estimator_weights[i_estimator] = estimator_weight
self.sample_weights = self.sample_weights * \
np.exp(- estimator_weight * np.ravel(y_pre) * np.ravel(self.y)) / self.sample_weights.sum()
# def predict_vec(self, vec):
# predict_vec = [i.predict(vec.reshape()) for i in self.estimators]
# value = sum(predict_vec * self.estimator_weights)
# if value > 0:
# return 1
# else:
# return -1
def predict(self, X):
result_matrix = np.array([i.predict(X) for i in self.estimators]).T
result_vec = (result_matrix * self.estimator_weights).sum(axis=1)
return np.where(result_vec >= 0, 1, -1)
# if len(X.shape) == 1:
# return self.predict_vec(X)
# else:
# return_ = np.zeros(X.shape[0])
# for i in range(len(X)):
# return_[i] = self.predict_vec(X[i])
def score(self, y_true, y_pre):
return (y_true.ravel() == y_pre.ravel()).sum() / len(y_true)
if __name__ == '__main__':
X, y = make_classification(n_samples=1000, n_features=4,
n_informative=2, n_redundant=0,
random_state=0, shuffle=False)
ada = AdaboostClassifier(X, y)
ada.fit()
ada_sklearn = ADASklern().fit(X, y)
print(f"本例准确率：{ada.score(ada.y, ada.predict(X))}")
print(f"sklearn准确率：{ada_sklearn.score(X,y)}")
本例准确率：0.96
sklearn准确率：0.975
回归
回归与分类的流程类似，主要有以下几个区别
- 错误率e
回归的错误率首先计算预测值与实际值的偏差，然后归一化，然后有三种处理方式，分别是线性误差、平方误差和指数误差：
\[E_k= max|y_i - G_k(x_i)|\;i=1,2...m
\]
\[e_{ki}= \frac{|y_i - G_k(x_i)|}{E_k}
\]
\[e_{ki}= \frac{(y_i - G_k(x_i))^2}{E_k^2}
\]
\[e_{ki}= 1 - exp（\frac{-|y_i - G_k(x_i)|}{E_k}）
\]
- 模型权重\(\alpha\)
\[\alpha_k =\frac{e_k}{1-e_k}
\]
- 样本权重
\[w_{k+1,i} = \frac{w_{ki}}{Z_k}\alpha_k^{1-e_{ki}}
\]
- 结合策略
\[\sum ln(\frac 1{\alpha_k})g(x)
\]
其中\(g(x)\)是\(\alpha_kh_k(x)\)的中位数
sklearn中使用的是按权重加权平均。
