随机森林：原理及python实现
Table of Contents
随机森林概述
如图所示,随机森林是一种使用Bagging(Bootstrap Aggregating)方法的集成模型(Ensemble Model).其基本思路是,将基模型看作定义在相应模型空间里的随机变量,通过取得独立同分布的不同模型来投票决定最终的预测结果.随机森林的基模型是决策树,整个过程中,会训练多个决策树模型,然后融合模型预测的结果给出一个预测结果.
集成模型有两个关键部分:基模型和结合策略
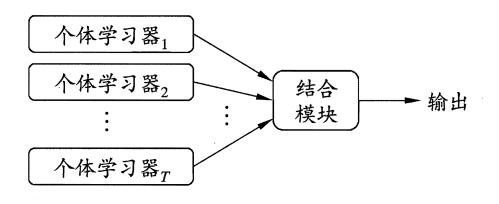
个体学习器
个体学习器可以分为同质和异质两种：
- 同质指的是不同个体学习器属于同一种类，比如都是决策树。
- 异质指的是个体学习器属于不同种类，比如既有决策树又有SVM。
目前来说，同质个体学习器的应用是最广泛的，一般我们常说的集成学习的方法都是指的同质个体学习器，而同质个体学习器使用最多的模型是CART决策树和神经元。
同质学习器按照个体学习器之间是否存在依赖关系可分为两类：
- 存在强依赖关系：学习器串行生成，即新学习器是在上一个学习器基础上生成的，代表就是boosting系列
- 不存在强依赖关系：学习器并行生成，各个学习器之间没有太大的依赖关系，代表就是bagging系列
集成策略
- 平均值：针对回归问题，对多个个体学习器的结果计算平均值作为最终结果，可以使用算数平均值、加权平均值等。
- 投票法：针对分类问题，对多个个体分类器的结果使用投票作为最终结果，可以使用少数服从多数、绝对多数、加权投票等。
- 学习法：对个体学习器结果再使用一个学习器来处理，即stacking
随机森林的一些相关问题
偏差（Bias）与方差(Variance)
假设某样本真实值为\(y\),\(f(x)\)为总体回归方程(PRF，Population Regression Function)，随机扰动\(\epsilon\sim N(0,\sigma^2)\)，且偏差与样本特征独立。\(\hat f(x)\)为样本回归方程(SRF,Sample Regression Function)，特征向量\(x\)，则有
\[y = f(x) + \epsilon
\]
使用MSE作为损失函数，有
\[\begin{split}l &= \frac 1n (y-\hat f(x))^2 \\& =E(y-\hat f(x))^2 \\&=Ey^2-2Ey\hat f(x)+E\hat f^2(x)\end{split}
\]
首先看第一项：
\[Ey^2 = E(f(x)+\epsilon)^2=Ef^2(x)+2E\epsilon f(x)+E\epsilon^2
\]
由于\(f(x)\)是PRF，对于总体数据而言，模型函数形式确定意味着PRF确定，因此，
\[Ef^2(x)=f^2(x)
\]
由于\(\epsilon\)与样本特征独立，因此，
\[E\epsilon f(x) = E\epsilon Ef(x)=0
\]
又有
\[E\epsilon^2=D\epsilon+(E\epsilon)^2=\sigma^2
\]
故
\[Ey^2 = f^2(x) + \sigma^2
\]
然后第二项：
由于SRF受样本影响，本质上是一个随机变量，因此，
\[-2Ey\hat f(x)=-2E(f(x)+\epsilon)\hat f(x)=-2f(x)E\hat f(x)
\]
最后第三项：
\[E\hat f^2(x) = D\hat f(x) + (E\hat f(x))^2
\]
把以上代入原式得
\[\begin{split}l &= f^2(x)-2f(x)E\hat f(x)+(E\hat f(x))^2 + D\hat f(x)+\sigma^2\\&=[f(x)-E\hat f(x)]^2+D\hat f(x)+\sigma^2\\&=Bias^2+Variance+\sigma^2\end{split}
\]
也就是说，实际值与真实值的偏差由三部分组成：SRF的方差、SRF的偏差以及随机扰动。在随机森林中，SRF就是一个一个的个体分类器（决策树）。
Bias代表模型的准确度，模型越复杂，Bias越低。Variance代表模型的不同程度，模型越复杂，越容易过拟合，不同样本训练出的SRF差别越大，Variance也就越大，如下图所示。因此，想要降低偏差平方和，可以从降低偏差、降低方差两个方面着手。
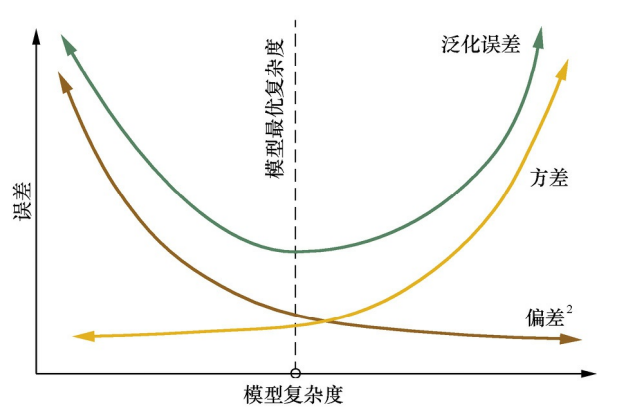
RF通过降低方差提高预测准确性
前面说到，Bagging通过训练多颗独立同分布的决策树，然后对其取平均作为预测结果，以此获得更准确的结果。为什么要追求独立同分布呢？首先，决策树模型同分布自不必多说，每颗树（SRF）都是由于不同的样本获取到的PRF的近似。
对于同分布的\(n\)个随机变量\(X_i,i=1,2,3,...,n\).其均值的方差
\[D\frac {\sum_{i=1}^nX_i}{n} = \frac 1{n^2}D\sum X_i=\frac 1{n^2}(nDX_i+\sum\limits_{k=1}^n\sum\limits_{j=k}^nCOV(X_k,X_j))=\frac 1{n^2}(n\sigma^2+n(n-1)\rho\sigma^2)=\frac {\sigma^2}n+\frac{n-1}{n}\rho\sigma^2=\rho\sigma^2+\frac{(1-\rho)\sigma^2}n
\]
在随机森林中，随机变量数量\(n\)代表决策树的数量，可以看出，随着树的数量\(n\)的增大，方差减小。在树的棵树一定时，相关系数\(\rho\)越大，方差越大，当\(\rho=0\)时，方差最小。因此，各颗树越不相关，方差越小。
注意:这里的\(\sigma\)指的是不同的树预测值的方差，即上文中的\(D\hat f(x)\)，与上面的随机扰动\(\epsilon\)的方差不同。
Bootstrap(自助采样)
顾名思义，随机森林使用了Bagging(Bootstrap Aggregating)方法，自然也就使用了Booststrap，其流程如下：
每颗树训练时，对于样本容量为\(m\)的训练集，有放回地从中抽取\(m\)个样本，作为这棵树的训练集合。当样本容量\(m\)足够大时，大约有36.8%的样本未被取到：
\[P = (1-\frac 1m)^m
\]
\[\lim\limits_{m \rightarrow+\infty}P =\frac 1e
\]
自助采样过程还给 Bagging 带来了另一个优点：由于每个基学习器只使用了初始训练集中约63.2％的样本，剩下约36.8％的样本可用作验证集来对泛化性能进行“包外估计 ”(out-of-bag estimate)。oob可以用来在决策树生长的过程中来辅助剪枝。
特征采样
随机森林对Bagging方法的一个小小改进就是不仅对样本进行自助采样，同时对特征进行了随机采样，通常情况下，采样特征数量\(k = log_2n\),\(n\)为特征数量
随机森林的实现
python实现
基于cart树的随机森林，不知道哪里有问题，有带佬发现了麻烦指教一下（不管了，编码一直是弱项ORZ，自己实现一方面是为了练习coding能力，另一方面主要还是为了加深对算法的理解）。
from sklearn.metrics import r2_score
from multiprocessing import Pool
import numpy as np
import sklearn.ensemble
from sklearn.datasets import load_diabetes
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings('ignore')
class DTNode:
'''
定义节点类用于存储决策树节点。
'''
def __init__(self, data):
# 用于存储节点数据
if len(data.shape) == 1:
self.data = data.reshape([1, -1])
else:
self.data = data
# 最优划分特征index
self.best_feature = None
# 节点划分特征数据类型
self.feature_type = None
# 节点划分条件
self.judge_value = None
# 左子节点
self.left_node = None
# 右子节点
self.right_node = None
# 节点划分后SE
self.se_split = np.inf
# 节点划分前SE
self.se_node = np.sum((data[:, -1] - np.mean(data[:, -1])) ** 2)
# 节点均值
self.value = np.mean(self.data[:, -1])
# 是否叶节点
self.leaf = False
# 随机采样到的列索引，只有根节点不是None
self.chosen_columns = None
class RandomForestRegressor:
def __init__(self, X, y, n_estimators=20, min_mse=1,
oob=False, feature_size=None):
self.features = np.array(X).reshape(len(X), -1)
self.labels = np.array(y).reshape(len(y), -1)
self.data = np.hstack([self.features, self.labels])
# 决策树数量
self.n_estimators = n_estimators
# 最小MSE，MSE低于这个值不再进行节点划分
self.min_mse = min_mse
self.oob = oob
# 特征采样数量
if feature_size is None:
self.feature_size = np.int32(np.log2(self.features.shape[1]))
else:
self.feature_size = feature_size
# 用于存储随机森林，训练完成后，决策树被存在长为n_estimator的列表里
self.forests = None
def bootstrap(self, data, oob=None):
'''
自助采样
:param data: 待采样数据，最后一列为标签的增广矩阵
:param oob: 是否保留袋外值，用于剪枝，暂时未使用
:return: 自助采样后的数据集
'''
X = np.array(data).reshape(len(data), -1)
if oob is None:
oob = self.oob
chosen_index = np.random.randint(0, len(data), len(data))
if oob is True:
oob_index = list(set(range(len(data))) - set(chosen_index))
return data[chosen_index, :], data[oob_index, :]
else:
return data[chosen_index, :]
def choose_feature(self, data):
'''
特征选择
:param data: 带有标签的增广矩阵
:return: 采样后增广矩阵,采样特征所在列索引（一维数组，包括y）
'''
data = np.array(data).reshape(len(data), -1)
if data.shape[1] == 2:
return data
else:
size = self.feature_size
chosen_col = np.random.randint(0, data.shape[1]-1, size)
chosen_col = np.append(chosen_col, data.shape[1]-1)
return data[:, chosen_col], chosen_col
def isCategorical(self, vec):
'''
判断是否为分类变量
:param vec: 待判断数据列
:return: True为分类变量，False为连续变量
'''
vec = np.array(vec)
if all(np.int32(vec) == vec):
return True
else:
return False
def calSE(self, array):
'''
计算输入数组的偏差平方和
:param array:数组
:return: 输入数组与均值的偏差平方和
'''
return np.sum((array - np.mean(array)) ** 2)
def bestSplitCat(self, X, y, index):
'''
节点使用分类变量特征最优划分方法
:param X: 特征矩阵
:param y: 标签向量
:param index:划分特征所在列索引
:return: node类实例，使用最优划分后的节点
'''
data = np.hstack([X, y])
node = DTNode(data)
node.best_feature = index
node.feature_type = 'Categorical'
diff_val = np.unique(data[:, index])
# 如果分类变量只有一个值，那么将节点标记为叶节点并返回
if len(diff_val) == 1:
node.leaf = True
return node
# 如果标签数据只有一个值，也就是偏差平方和为0，标记为叶节点并返回
if len(np.unique(y)) == 1:
node.leaf = True
return node
# 遍历所有可能的二划分方法，如果划分后的偏差平方和小于当前节点偏差平方和，则更新节点信息
for i in range(1, 2 ** len(diff_val)-1):
bin_i = bin(i)[2:]
len_i = len(bin_i)
num_zero = len(diff_val) - len_i
if num_zero < 0:
num_zero = 0
final_i = '0' * num_zero + bin_i
chosen_index = np.array([int(j) for j in final_i])
chosen_value = diff_val[chosen_index.astype(bool)]
filter_ = np.in1d(X[:, index], chosen_value)
left_node = data[filter_]
right_node = data[~filter_]
SE = self.calSE(left_node[:, -1]) + self.calSE(right_node[:, -1])
if SE < node.se_split:
node.left_node = DTNode(left_node)
node.right_node = DTNode(right_node)
# 对于分类变量，judge_value第一个值是左节点中的值，第二个是右节点中的值
node.judge_value = [chosen_value,
np.setdiff1d(diff_val, chosen_value)]
node.se_split = SE
# 如果划分后偏差平方和仍然大于等于节点偏差平方和，那么标记为叶节点
if node.se_split >= node.se_node:
node.leaf = True
return node
def bestSplitCon(self, X, y, index):
'''
连续变量特征的最优划分方法
:param X: 特征矩阵
:param y: 标签向量
:param index: 待划分特征所在列索引
:return:node类实例，使用划分后的最优节点
'''
data = np.hstack([X, y])
node = DTNode(data)
node.best_feature = index
node.feature_type = 'Continuous'
feature_data = X[:, index]
sorted_feature = sorted(feature_data)
thresholds = [np.mean([sorted_feature[j], sorted_feature[j+1]])
for j in range(len(sorted_feature)-1)]
if len(np.unique(feature_data)) == 1:
node.leaf = True
return node
for thresh in thresholds:
filter_ = feature_data > thresh
left_node = data[filter_]
right_node = data[~filter_]
SE = self.calSE(left_node[:, -1]) + self.calSE(right_node[:, -1])
if SE < node.se_split:
node.left_node = DTNode(left_node)
node.right_node = DTNode(right_node)
node.se_split = SE
node.judge_value = thresh
return node
def fit_regression_tree(self, node_data, chosen_columns=None):
'''
训练一颗决策树
:param node_data: 输入的特征采样后的数据
:param chosen_columns: 特征采样的列索引，预测时使用
:return:node类对象实例，决策树根节点
'''
X = np.array(node_data[:, :-1]).reshape(len(node_data), -1)
y = np.array(node_data[:, -1]).reshape(len(node_data), -1)
data = np.hstack([X, y])
node = DTNode(data)
node.chosen_columns = chosen_columns
if len(node_data) == 1:
node.leaf = True
return node
if node.se_node < node.data.shape[0] * self.min_mse:
node.leaf = True
return node
if len(np.unique(y)) == 1:
node.leaf = True
return node
if len(np.unique(X, axis=0).reshape(-1, X.shape[1])) == 1:
node.leaf = True
return node
for i in range(X.shape[1]):
if self.isCategorical(X[:, i]):
n = self.bestSplitCat(X, y, i)
if n.se_split < node.se_split:
node = n
node.chosen_columns = chosen_columns
else:
n = self.bestSplitCon(X, y, i)
if n.se_split < node.se_split:
node = n
node.chosen_columns = chosen_columns
# if node.se_split == np.inf:
if node.leaf is True:
return node
node.left_node = self.fit_regression_tree(node.left_node.data)
node.right_node = self.fit_regression_tree(node.right_node.data)
return node
def fit_forest(self, ind):
data = self.bootstrap(self.data)
data, columns = self.choose_feature(data)
return self.fit_regression_tree(data, columns)
def fit(self):
with Pool() as p:
forests = p.map(self.fit_forest, list(range(self.n_estimators)))
self.forests = forests
def tree_predict(self, vec, node):
if node.leaf is True:
return node.value
else:
if node.feature_type == 'Categorical':
if vec[node.best_feature] in node.judge_value[0]:
next_node = node.left_node
else:
next_node = node.right_node
elif vec[node.best_feature] > node.judge_value:
next_node = node.left_node
else:
next_node = node.right_node
return self.tree_predict(vec, next_node)
def predict_vec(self, vec):
vec = np.array(vec)
l = []
for node in self.forests:
vec_ = vec[node.chosen_columns[:-1]]
l.append(self.tree_predict(vec_, node))
return np.mean(l)
def predict(self, data):
if len(data.shape) == 1:
return self.predict_vec(data)
else:
r = []
for i in data:
r.append(self.predict_vec(i))
return r
if __name__ == '__main__':
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
rf = sklearn.ensemble.RandomForestRegressor().fit(X, y)
pre = rf.predict(X)
score = mean_squared_error(pre, y)
print(f"sklearn的MSE:{score}")
print(f"sklearn的可决系数:{r2_score(pre,y)}")
print()
rfm = RandomForestRegressor(X, y, 20)
rfm.fit()
p = rfm.predict(X)
print(f"自写的MSE:{mean_squared_error(p, y)}")
print(f"自写的可决系数:{r2_score(p,y)}")
sklearn的MSE:483.6802142533937
sklearn的可决系数:0.8779661780599455
自写的MSE:730.1600067207331
自写的可决系数:0.7926145660075448
Sklearn实现
随机森林分类的一个例子
下面的例子是一个使用随机森林进行分类的示例：
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
#在two_moon数据集上构造5棵树组成的随机森林
import seaborn as sns
import mglearn
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
X,y = make_moons(n_samples=100,noise=0.25,random_state=3)
X_train,X_test,y_train,y_test = train_test_split(X,y,stratify=y,random_state=42)
RFC = RandomForestClassifier(n_estimators=100,random_state=2).fit(X_train,y_train)
# 将每棵树及总预测可视化
fig,axes = plt.subplots(2,3,figsize=(20,10))
for i,(ax,tree) in enumerate(zip(axes.ravel(),RFC.estimators_)):
ax.set_title('Tree{}'.format(i))
mglearn.plots.plot_tree_partition(X_train,y_train,tree,ax=ax)
mglearn.plots.plot_2d_separator(RFC,X_train,fill=True,ax=axes[-1,-1],alpha=.4)
axes[-1,-1].set_title('Random Forest')
mglearn.discrete_scatter(X_train[:,0],X_train[:,1],y_train)
plt.show()
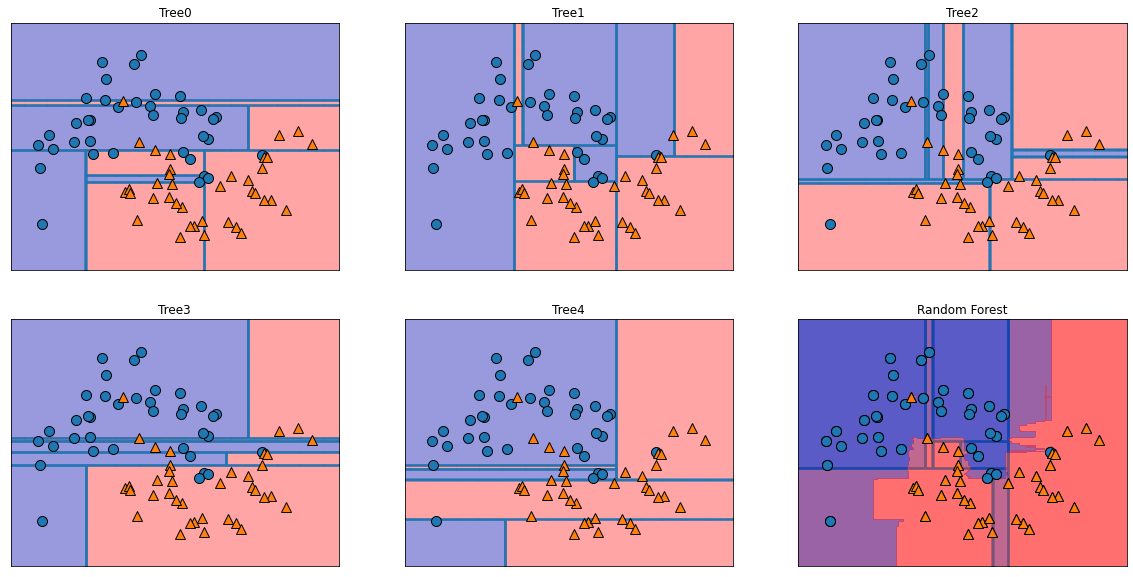
可以看出，随机森林也是实现了曲线边界
使用oob
# 在乳腺癌数据上构建随机森林
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train,X_test,y_train,y_test=train_test_split(cancer.data,cancer.target,stratify=cancer.target,random_state=0)
RFC = RandomForestClassifier(n_estimators=100,max_features=5,oob_score=True,random_state=88).fit(X_train,y_train)
print('训练精度：{}'.format(RFC.score(X_train,y_train)))
print('测试精度：{}'.format(RFC.score(X_test,y_test)))
print('袋外分数：{}'.format(RFC.oob_score_))
训练精度：1.0
测试精度：0.958041958041958
袋外分数：0.9624413145539906
特征重要性
随机森林的特征重要性，sklean使用的是跟之前提到的决策树的特征重要性相同，只是对不同树的特征重要性取了平均值。
fig = plt.figure(dpi=100)
plt.barh(range(len(RFC.feature_importances_)),RFC.feature_importances_)
plt.yticks(range(len(RFC.feature_importances_)),cancer.feature_names)
plt.xlabel("Feature Importance")
plt.show()
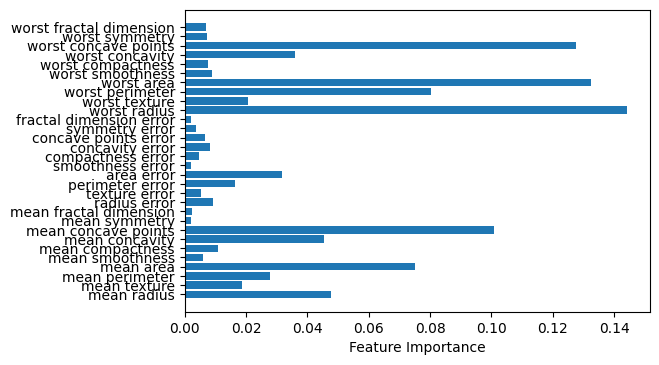
随机森林的推广
extra tree
Extra Tree与Random Forest十分类似，区别就是Extra Tree不使用boostrap对样本进行随机采样，但是，在选择特征的时候，随机在所有特征中选择一个进行特征划分。这进一步增强了树之间的独立性，但是会导致偏差增大。
from sklearn.ensemble import ExtraTreesClassifier
ETC = ExtraTreesClassifier(n_estimators=100,random_state=88).fit(X_train,y_train)
print('训练精度：{}'.format(ETC.score(X_train,y_train)))
print('测试精度：{}'.format(ETC.score(X_test,y_test)))
训练精度：1.0
测试精度：0.9370629370629371
TRTE(Totally Random Trees Embedding，数据转换方法)
TRTE是一种非监督的数据转换方法。其原理是，比如，训练10棵树，每棵树都有5个叶节点，对于一条样本，在某棵树中被分配到第3个叶节点中，那这个样本点在这棵树的表示就是（0，0，1，0，0），使用One-Hot表示，然后，将10棵树的样本向量拼接起来，即得到转换后的样本向量。与FB经典的gbdt+lr算法十分类似。
如下所示，选用了10棵树构建的随机森林，由于没有限制最大叶子节点数，因此，不同树的叶节点数量不同，X_train原始为\(426\times30\)的矩阵，转换后变成了\(426*176\)的矩阵。sklearn中RandomTreesEmbedding类在fit时没有y，它的y是使用np.uniform生成的在0-1上的服从均匀分布的向量，长度跟X相同。也就是说，在构建树时，随机挑选特征构建。
from sklearn.ensemble import RandomTreesEmbedding
display(X_train.shape)
RTE = RandomTreesEmbedding(n_estimators=10,random_state=50).fit(X_train)
r = RTE.transform(X_train)
r
(426, 30)
<426x176 sparse matrix of type '<class 'numpy.float64'>'
with 4260 stored elements in Compressed Sparse Row format>
Isolation Forest（iForest，异常检测算法）
iFroest基于这样一种思想，如下图所示，对于非异常点\(x_i\)，周围的数据点比较多，使用决策树对其进行划分，当它进入叶节点时，通常需要经过更多的层数。而异常点，如下\(x_o\),在比较浅层的时候就被分入了叶节点。因此，所在叶节点越“浅”，越有可能是异常点。
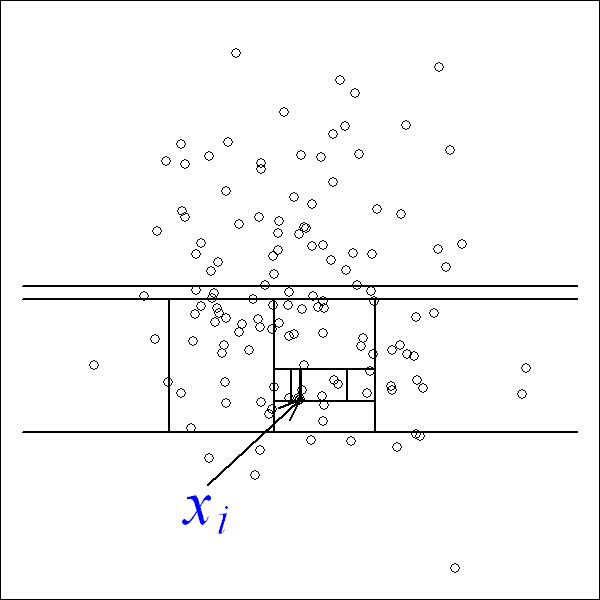
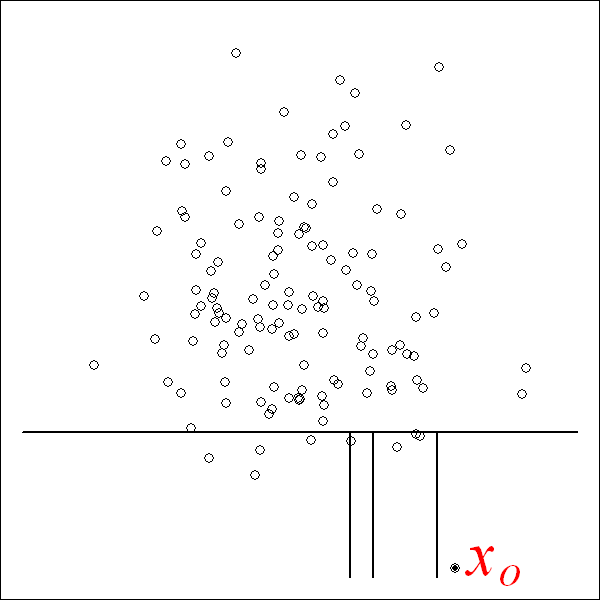
对于某样本点，其为异常值的概率可以表示为：
\[s(x,m) = 2^{-\frac{h(x)}{c(m)}}
\]
其中:
\[c(m) = 2H(m-1)-\frac{2(m-1)}n
\]
H(i)可近似估算：
\[H(i) = ln(i)+\xi ；\xi为欧拉常数
\]
\(h(x)\)——样本x的叶节点所在树深均值
\(c(m)\)——样本量为m的数据集，样本点所在叶节点深度的均值
from sklearn.ensemble import IsolationForest
X = [[-1.1], [0.3], [0.5], [100]]
clf = IsolationForest(random_state=0).fit(X)
clf.predict([[0.1], [0], [90]])
array([ 1, 1, -1])
