决策树:原理以及python实现
Table of Contents
决策树概述
决策树的决策方式
如下图所示,决策树的决策过程本质上是一系列的if/then语句,通过学习到的规则来做出决策。在下图的邮件分类应用中,我们的规则是如果邮件来自myEmployer.com那么邮件就被分类为“无聊的时候再读”,否则再判断邮件内容是否包含“曲棍球”,如果是,那么就是来自朋友的邮件,被分类为“立刻阅读”,否则被分类为“垃圾邮件”。
显然,决策树的决策规则具有一个重要性质:互斥且完备。这意味着,对于每一个样本,有且只有一条路径使其从根节点走到某个叶节点。同时,由于对样本特征不断的进行一系列的条件\(X_i\)的判断,决策树也可以理解为对\(P(y_i|X_i)\)的条件概率的求解。比如下面这个例子可以理解为,在邮件来自myEmployer.com时,邮件属于“无聊的时候再读”的概率是100%。
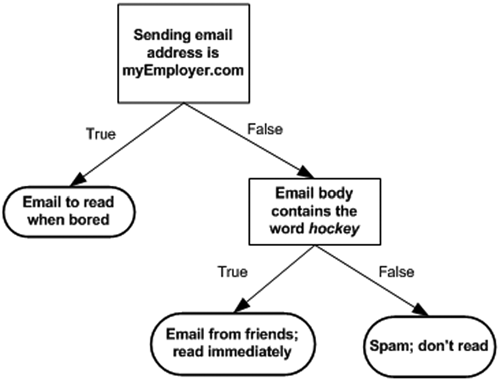
决策树的规则学习过程
为了构造决策树,算法遍历所有可能询问的问题,找出对于目标变量来说信息量最大的一个,将数据集分为两部分,重复此过程直到结束,其原理如下:
输入:训练集\(D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}\)
属性集\(A=\{a_1,a_2,a_3,...,a_n\}\)
createBranch()方法:
检测数据集\(D\)中的所有数据的分类标签\(A\)是否相同:
If so return 类标签
Else:
从A中寻找最优划分特征
划分数据集
创建分支节点
for 每个划分的子集
调用函数 createBranch(创建分支的函数)并增加返回结果到分支节点中
return 分支节点
特征选择
上一节说到,决策树在划分节点时,选择一个最佳特征将样本数据划分到不同的节点中,那么,该如何选择最优特征呢?
信息熵
第二节中的算法中,某个节点停止划分成为叶节点的条件是,节点内所有样本均属于同一类别。也就是节点是“纯净的”。因此,在选择特征进行划分时,使得节点越纯净的特征就是越好的特征。我们使用信息熵(Entropy)来衡量一组样本的“纯净度”。
对于离散型随机变量X,其分布为:
则其信息熵为
那么为什么信息熵能够衡量纯净度呢?
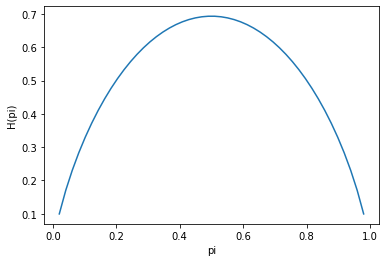
二分类
首先,考虑二分类,即
则有
当\(\frac12\leq p_i\leq1\)时,\(H'(p_i)\leq0\),\(H\)递减。
当\(0\leq p_i\leq\frac12\)时,\(H'(p_i)\leq0\),\(H\)递增。
当\(p_1=\frac 12\)时,信息熵有最大值。
如下图所示,也就是说,信息熵越大,两个类别的样本数量也就越接近。举一个极端的例子,A类样本50%,B类样本50%的节点纯净程度显然不如A类100%,B类0%的节点纯净度。也就是说,可以认为,信息熵越大,节点的“纯净度”就越低。因此,对于二分类,信息熵越小越好。
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
x = np.linspace(0,1)
y = -x*np.log(x)-(1-x)*np.log(1-x)
plt.xlabel('pi')
plt.ylabel('H(pi)')
plt.plot(x,y)
plt.show()
多分类
对于多分类,同样的有这样一个结论:对于\(H(X) = - \sum\limits_{i=1}^kp_ilnp_i,\sum\limits_{i=1}^kp_i=1\),当\(p_i=\frac 1k\)时,信息熵\(H\)有最大值。
约束条件下的极值很自然的想到使用拉格朗日乘数法证明:
还有一个有意思的证明:http://www.math345.com/blog/article/17
信息增益
上一节中提到了使用信息熵来衡量叶节点的纯净度,很自然的,在最优特征选择的时候,可以选择使得信息熵变得最小的特征作为最优特征。
信息增益(Information Gain):特征\(A\)对于节点数据\(D\)的信息增益
可以看出,由于信息熵的绝对大小只与变量的分布有关。因此,在划分了多个节点之后,使用每个节点的样本数量占上一级节点样本数的比例作为权重对信息熵进行加权,然后计算加权信息熵与划分前的信息熵的差,作为信息熵的增量,也就是信息增益。
信息增益比
使用信息增益作为划分数据集的特征,偏向于选择类别多的特征。考虑一个极端的二分类问题,假设当前节点有20个样本,正负样本各占一半,某个特征\(A\)刚好有20个类别,将其划分为20个纯净的节点,信息增益达到最大。另一个特征\(B\)只将训练数据划分为2个节点,并且节点不纯净。按照信息增益准则,将选择特征\(A\)作为划分特征,但是,在预测时,特征\(A\)很可能因为过拟合而泛化性能变低。因此,可使用信息增益比作为划分标准。
由于对于
当\(p_i=\frac 1k\)时候,有
也就是说,随着随机变量\(X\)类别的增加\(H_{max}\)是增加的。因此,可以用信息增益与特征\(A\)的固有值\(IV\)之比来作为划分标准。但是,根据周志华老师的说法,信息增益比会偏好分类类别较少的特征,这应当是由固有值增长的速度较快导致的。
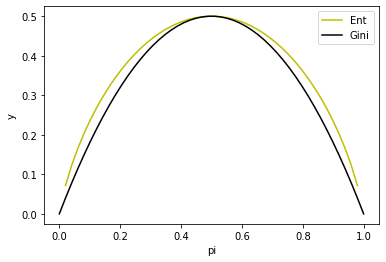
基尼系数
定义基尼系数:
基尼系数表示的是在一个节点中,随机选取两个样本点,其类别不同的概率。节点越纯净,概率就越低。如下所示是在二分类的情况下,Gini系数与信息熵的一半(以2为底)的图像。可以看出,二者十分相似。可以采用第一节中的方法证明,gini系数与信息熵有类似的性质。
x = np.linspace(0,1)
ent = (-x*np.log2(x)-(1-x)*np.log2(1-x))/2
gini = 2*x*(1-x)
plt.xlabel('pi')
plt.ylabel('y')
plt.plot(x,ent,c='y',label='Ent')
plt.plot(x,gini,c='black',label='Gini')
plt.legend()
plt.show()
ID3
算法流程
ID3是经典的机器学习算法,使用信息增益选择划分特征。其方法是:从根节点开始,计算所有可能的特征的信息增益,然后选择信息增益最大的特征对节点进行划分。然后递归地对每一个节点使用此划分方法,直到信息增益为0或小于阈值,或无可用特征。
在进行预测时,只需按照已经构建好的树逐一判断条件,将待预测样本分入相应的叶节点中,然后选择节点中类别较多的类别作为预测类别。
Python实现
这里实现的是完全生长的决策树,可以增加阈值\(\epsilon\),当信息增益\(G<\epsilon\)时,即停止生长。
import collections
import numpy as np
class ID3:
def __init__(self, X, y, feature_name):
self.features = X
self.labels = y
self.data = np.hstack((self.features, self.labels))
self.feature_label = feature_name
self.tree = {}
def calEntropy(self, data):
'''
计算信息熵
:param data:列表等序列
:return:输入数据的信息熵
'''
entropy = 0
c = collections.Counter(np.array(data).ravel())
total = len(data)
for i in c.values():
entropy -= i/total * np.log(i/total)
return entropy
def splitdata(self, data, col, value):
'''
:param data:
:param col:待划分特征列的数字索引
:param value:
:return:返回输入data的col列等于value的去掉col列的矩阵
'''
data_r = data[data[:, col] == value]
data_r = np.hstack((data_r[:, :col], data_r[:, col+1:]))
return data_r
def getBestFeature(self, data):
'''
:param data: 形式为[X y]的矩阵
:return: 最优特征所在列索引
'''
entropy_list = []
numberAll = data.shape[0]
for col in range(data.shape[1]-1):
entropy_splited = 0
for value in np.unique(data[:, col]):
y_splited = self.splitdata(data, col, value)[:, -1]
entropy = self.calEntropy(y_splited)
entropy_splited += len(y_splited)/numberAll*entropy
entropy_list.append(entropy_splited)
return entropy_list.index(min(entropy_list))
def CreateTree(self, data, label):
'''
:param data: 形如[X y]的矩阵
:param feature_label:
:return: 决策树字典
'''
feature_label = label.copy()
if len(np.unique(data[:, -1])) == 1:
return data[0, -1]
if data.shape[1] == 1:
return collections.Counter(data[:, -1]).most_common()[0][0]
bestFeature = self.getBestFeature(data)
bestFeatureLabel = feature_label[bestFeature]
treeDict = {bestFeatureLabel: {}}
del feature_label[bestFeature]
for value in np.unique(data[:, bestFeature]):
sub_labels = feature_label[:]
splited_data = self.splitdata(data, bestFeature, value)
treeDict[bestFeatureLabel][value] = self.CreateTree(splited_data, sub_labels)
return treeDict
def fit(self):
self.tree = self.CreateTree(self.data, self.feature_label)
def predict_vec(self, vec, input_tree=None):
if input_tree==None:
input_tree = self.tree
featureIndex = self.feature_label.index(list(input_tree.keys())[0])
secTree = list(input_tree.values())[0]
vec_feature_val = str(vec[featureIndex])
if type(secTree.get(vec_feature_val)) != dict:
return secTree.get(vec_feature_val)
else:
return self.predict_vec(vec, secTree.get(vec_feature_val))
def predict(self, X):
out_put=[]
for i in X:
out_put.append(self.predict_vec(i))
return out_put
def main():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
X = np.array(dataSet)[:, :-1]
y = np.array(dataSet)[:, -1].reshape(-1, 1)
id3 = ID3(X, y, labels)
id3.fit()
print(id3.tree)
print(id3.predict_vec([1, 0]))
print(id3.predict(X))
if __name__ == '__main__':
main()
{'no surfacing': {'0': 'no', '1': {'flippers': {'0': 'no', '1': 'yes'}}}}
no
['yes', 'yes', 'no', 'no', 'no']
小结
ID3在当时提出了一个新的思路,但是仍然有很多问题。比如,只能处理分类变量,每个特征只能使用一次,信息增益偏好类别多的特征,容易过拟合等。
C4.5
C4.5是对ID3的改进,李航老师的《统计学习方法》中提到的改进,只有使用了信息增益比来代替信息增益。@刘建平Pinard 老师的博客中,提到了一些其他的优化方法也是C4.5所采用的。总体有以下几个方面:
连续值的处理
连续值采用机器学习中常用的方法:连续变量离散化,即对连续值进行分箱操作。决策树算法中,选定一个阈值,将连续变量分为两类,大于阈值的属于类别1,小于阈值的属于类别0。具体方法如下,对于输入矩阵\(X_{m\times n}\),某连续特征\(A\)的取值从小到大排列为序列\(a_1,a_2,...,a_m\),考察包括\(m-1\)个划分点的集合
也就是分别选取两个相邻值得中位数作为划分阈值,将特征映射为两个类别。然后按照前面所说得离散变量的处理方法,选择信息增益最大的划分方法。
特征选择
ID3使用的是前面提到的信息增益作为划分标准,C4.5使用了前面提到的信息增益比。周志华老师书中提到,信息增益比偏好划分类别较少的特征,信息增益偏好类别较多的特征,因此,可以先选取信息增益高于平均值的特征,然后再从中选择信息增益率最高的特征。
缺失值的处理
在构造决策树的时候,对于有缺失值的特征的处理,需要解决以下两个问题:
- 如何在属性值缺失的情况下进行划分属性选择?
- 给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?
问题1
对于节点,样本集合为\(D\),假设某特征\(A\)有部分缺失,用\(D_{缺失}\)代表特征\(A\)缺失的样本集合,\(D_{未缺失}\)代表属性\(A\)未缺失的集合。在计算属性\(A\)的信息增益时,使用\(D_{未缺失}\)计算信息增益\(G_{未缺失}\),然后,乘以一个权重作为最终的信息增益。
可以看出,这个方法的思路是,使用未缺失的那部分样本来计算信息增益。但是由于只使用了部分数据,在跟其他特征“竞争”最优特征的时候是不公平的。因此,对这个信息增益乘以一个权重,做一个缩小,以减弱缺失特征的“竞争力”,这个权重使用的是特征\(A\)的“完备率”,也就是说,缺失越严重,信息增益越低,这个特征也就越不可能被选为最优特征。
问题2
上一个问题解决了选择最优特征的时候缺失值的处理方法,如果\(A\)特征没被选为最优特征,那缺失值对之后的数据划分并没有影响。但是,当特征\(A\)被选为最优划分特征的时候,缺失值的样本该划分到哪个分支中呢?
这里,选择将含有缺失值的样本同时划分到所有分支中,但是,每个样本并不是完整的样本,而是样本的“一部分”。在计算集合信息熵的时候,每个类别的概率\(p_k\)使用的其实是古典概型的频率,比如,节点共有100个样本,属于类别1的样本有70个,每个样本的权重都是1,则\(p_1=0.7\)。而对于进入这个节点的“一部分样本”却不能占有1的权重,只能占有一部分权重。这个权重就是缺失样本进入该节点的期望权重,也就是进入该节点的概率,也就是进入该节点的样本点数量与总数量之比。
举个例子,某个节点共100个样本,其中特征\(A\)缺失的有20个,根据特征\(A\)进行了划分,其中节点1有30个样本,节点2有50个样本。在对缺失的20个样本划分的时候,每个样本都进入了节点1和2,也就是说,节点1中最终有50个样本,节点2中有70个样本。但是在节点1中,含缺失值的样本的权重不是1,而是0.375,同理,在节点2中,这些样本的权重是0.625。
同理,在进行预测时,如果输入变量某特征缺失,则采用同样的方法,最终样本点可能被分配到不同的节点中,对节点按照节点概率\(P\)以及前面所说的权重加权即可。
剪枝的策略
充分生长的决策树由于复杂度很高,很容易对训练集过拟合,导致泛化能力差。因此,需要控制决策树复杂度,降低过拟合程度,提高泛化能力。其主要策略有两种:预剪枝和后剪枝。
预剪枝
预剪枝是指在决策树生成的过程中进行的剪枝操作。在每次划分节点时,通过对预先留出的验证集的预测精度的对比,决定是否要划分该节点。比如,在节点划分前,用决策树对验证集分类的准确度是80%,划分后只有70%,那么就会停止该节点的继续生长。
可以看出,预剪枝使得很多分支没有展开,这不仅降低了过拟合的风险,同时,使得决策树的训练时间显著降低。但是,由于预剪枝使用的是一种贪心算法,即虽然在本层划分不会提高精度,但是当节点二次划分的时候可能会提高精度,因此,可能会有欠拟合的风险。
后剪枝
后剪枝是一种先构建完整的决策树,再去除部分节点的方法。其方法是,构建一颗决策树,假设决策树深度为k,则第k层为叶节点,选择第k-1层的节点,去除其第k层划分,如果验证集精度上升,则删除该划分,否则保留。
不难看出,后剪枝比预剪枝更为优越,通常它会保留更多的节点并具有更强的泛化能力,但是,由于需要构建完整的树并且验证多个节点,模型的复杂程度会更高。
CART(Classification And Regression Tree)
分类树
CART分类树与前面的算法相比主要有以下几点不同:
- 特征选择:使用基尼系数作为特征选择标准,避免了大量对数计算。
- 特征划分:对于连续特征,使用的方法与C4.5相同,都是进行离散化二分,不同的是可以在后续继续使用。对于离散特征,也进行二分划分。
回归树
回归树与分类树的基本结构十分相似,主要有以下两个不同:
- 无论是基尼系数还是信息增益都是针对分类变量的评价方式,针对连续变量,要使用偏差平方和等。
- 预测时,分类树是使用每个节点内,样本数量最多的类别作为节点的预测类别,连续变量使用节点内样本均值作为预测值。
预测值的选择
对于每一个节点,为什么要选择均值作为预测值呢?
假设节点\(t\)的预测值为\(C_t\),节点有\(n\)个样本,则该节点的损失
则有
即对于所有的常数\(C_t\),使得损失\(L_t\)最小的常数就是均值。
特征选择
由于Cart是二叉树,在回归时,使用使得划分后的两节点的均方误差和最小的划分组合:
中括号内的最小化指的是针对某个具体的特征,在各种不同的切分节点(针对连续变量)或二分方式(针对离散变量)中,使得损失最小的那种,外层最小化指的是,针对不同的特征,选择最优的划分特征。
python实现
如下所示,这里实现了三个剪枝方法,分别是min_samples_split(某节点样本数小于该值时停止划分)、min_leaf_sample(划分后子节点小于该值舍弃此次划分)、min_impurity_decrease(划分后,偏差平方和增量绝对值小于该值舍弃此次划分)。这里min_impurity_decrease=0.01很小,没有起到作用,这时,可以看出,再最小划分数为4以及叶片最小样本数为4的情况下,MSE为0.02426与sklearn结果相同。
import numpy as np
import pandas as pd
import json
from sklearn.tree import DecisionTreeRegressor
class RegressionTree:
def __init__(self, X, y, min_samples_split=4, min_impurity_decrease=0.01, min_leaf_sample=4):
self.features = np.array(X).reshape(X.shape[0], -1)
self.labels = np.array(y).reshape(y.shape[0], -1)
self.data = np.hstack((self.features, self.labels))
self.min_samples_split = min_samples_split
self.min_impurity_decrease = min_impurity_decrease
self.min_leaf_sample = min_leaf_sample
def calSE(self, array):
'''
:param array:
:return: 输入数组与均值的偏差平方和
'''
return np.sum((array-np.mean(array))**2)
def bestFeatCat(self, data, index):
'''
这里在循环遍历的时候其实是遍历了两倍的数量
:param data: 输入矩阵,形式为[X y],其中y为连续变量,是回归的目标值
:param index: 类别变量所在的列索引
:return: 最小偏差平方和,最小偏差平方和对应的划分[list1,list2]
'''
best_split = []
best_se = np.inf
original_se = self.calSE(data)
uniqueVlaue = np.unique(data[:, index])
n = len(uniqueVlaue)
for i in range(1, 2**n-1):
chooseKey=[]
for j in range(n):
if (i >> j) % 2 == 1:
chooseKey.append(j)
filter = pd.Series(data[:, index]).isin(uniqueVlaue[chooseKey])
left_node = data[filter]
right_node = data[~filter]
if len(left_node) < self.min_leaf_sample:
continue
if len(right_node) < self.min_leaf_sample:
continue
SE = self.calSE(left_node[:, -1]) + self.calSE((right_node[:, -1]))
if SE < best_se:
best_se = SE
best_split = [uniqueVlaue[chooseKey], np.setdiff1d(uniqueVlaue, uniqueVlaue[chooseKey])]
if original_se - best_se < self.min_impurity_decrease:
return None, np.mean(data[:, -1])
return best_se, best_split
def bestFeatCon(self, data, index):
'''
大于阈值划分为左节点
:param data: 输入矩阵,形式为[X y],其中y为连续变量,是回归的目标值
:param index: 连续变量特征所在列索引
:return: 最小偏差平方和,最小偏差平方和对应的阈值
'''
sorted = data[:, index].copy()
sorted.sort()
threshold = []
best_se = np.inf
original_se = self.calSE(data)
best_split = None
for i in range(sorted.shape[0]-1):
avg = sorted[[i, i+1]].mean()
threshold.append(avg)
for j in threshold:
series = pd.Series(data[:, index])
filter = series > j
left_node = data[filter]
right_node = data[~filter]
if len(left_node) < self.min_samples_split:
continue
if len(right_node) < self.min_samples_split:
continue
SE = self.calSE(left_node[:, -1]) + self.calSE((right_node[:, -1]))
if SE < best_se:
best_se = SE
best_split = j
if best_se == np.inf:
return None, np.mean(data[:, -1])
if original_se - best_se < self.min_impurity_decrease:
return None, np.mean(data[:, -1])
return best_se, best_split
def chooseBestFeat(self, data):
'''
用于选择最优划分特征
:param data:输入矩阵,形式为[X y],其中y为连续变量,是回归的目标值
:return: 最优特征所在列的索引,最小的SE,最佳特征对应的划分(分类特征为)
'''
if len(data) <= self.min_samples_split:
return None, None, data[:, -1].mean(), None
best_feat = -1
best_se = np.inf
best_split = -1
for i in range(data.shape[1]-1):
if all(data[:, i].astype(int) == data[:, i]):
se = self.bestFeatCat(data, i)[0]
split = self.bestFeatCat(data, i)[1]
type = 'categorical'
else:
se = self.bestFeatCon(data, i)[0]
split = self.bestFeatCon(data, i)[1]
type = 'continuous'
if se is None:
continue
if (se < best_se) or (se is None):
best_feat = i
best_se = se
best_split = split
if best_se == np.inf:
best_feat = None
best_split = np.mean(data[:, -1])
return best_feat, best_se, best_split, type
def splitData(self, data, feature, values, FeatType):
if FeatType == 'categorical':
left = data[pd.Series(data[:, feature]).isin(values[0])]
right = data[pd.Series(data[:, feature]).isin(values[1])]
if FeatType == 'continuous':
left = data[pd.Series(data[:, feature]) > values]
right = data[pd.Series(data[:, feature]) <= values]
return left, right
def createTree(self, data):
'''
:param data:
:return:
'''
if len(data) <= self.min_leaf_sample:
return np.mean(data[:, -1])
feature, se, values, FeatType = self.chooseBestFeat(data)
if feature is None:
return values
tree = dict()
tree['splitInd'] = feature
tree['splitValue'] = values
tree['FeatType'] = FeatType
left, right = self.splitData(data, feature, values, FeatType)
tree['left'] = self.createTree(left)
tree['right'] = self.createTree(right)
return tree
def fit(self):
self.tree = self.createTree(self.data)
def predict_vec(self, x, tree=None):
x = np.array(x)
if tree is None:
tree = self.tree
if x[tree.get('splitInd')] > tree.get('splitValue'):
if isinstance(tree.get('left'), dict):
return self.predict_vec(x, tree.get('left'))
else:
return tree.get('left')
else:
if isinstance(tree.get('right'), dict):
return self.predict_vec(x, tree.get('right'))
else:
return tree.get('right')
def predict(self, data):
l = []
for i in data:
l.append(self.predict_vec(np.array(i)))
return np.array(l)
def calMSE(self, y_true, y_pre):
y_true = np.array(y_true)
y_pre = np.array(y_pre)
return np.mean((y_true-y_pre)**2)
if __name__ == '__main__':
data = pd.read_csv('./ex00.txt', sep='\t', header=None)
tree = RegressionTree(data[0], data[1])
a = tree.splitData(data.values, 0, 0.498035, 'continuous')[0]
b = tree.splitData(data.values, 0, 0.498035, 'continuous')[1]
tree.fit()
y_pre = tree.predict(data.iloc[:, 0].values.reshape(-1, 1))
print(f"MSE:{tree.calMSE(y_pre, data.iloc[:, -1])}")
dt = DecisionTreeRegressor(min_samples_split=4,
min_samples_leaf=4).fit(data.iloc[:, 0].values.reshape(-1, 1), data.iloc[:,1])
y_pre_dt = dt.predict(data.iloc[:, 0].values.reshape(-1, 1))
print(f"SKlearnMSE:{tree.calMSE(y_pre_dt, data.iloc[:, -1])}")
MSE:0.024262198879467293
SKlearnMSE:0.024262198879467293
多变量决策树
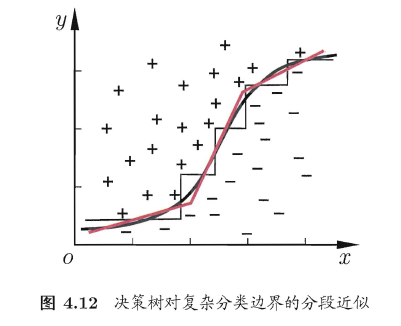
假设现在输入数据只有两个连续特征,且特征可重复使用。由于在划分的时候,划分条件是诸如\(FeatureA>40\),因此,如下图所示,使用决策树进行决策的过程,可以看作将二维平面不断使用垂直于两坐标轴的直线进行分割。
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import mglearn
X,y = make_moons(n_samples=100,noise=0.25,random_state=3)
X_train,X_test,y_train,y_test = train_test_split(X,y,stratify=y,random_state=42)
DSC = DecisionTreeClassifier().fit(X_train,y_train)
mglearn.plots.plot_tree_partition(X_train,y_train,DSC)
plt.show()
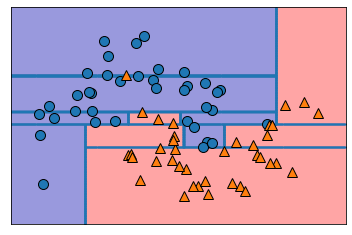
如下图所示,多变量决策树改变了\(FeatureA>40\)的划分方式,使用诸如
的方法进行划分,使得决策边界可以是倾斜的直线或曲线。
Sklearn决策树
sklearn构造决策树
# 使用乳腺癌数据集构造决策树
from sklearn.datasets import load_breast_cancer
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train,X_test,y_train,y_test = train_test_split(cancer.data,cancer.target,stratify=cancer.target,random_state=42)
##使用乳腺癌数据集构造决策树
DTC =DecisionTreeClassifier(max_depth=3).fit(X_train,y_train)
print('训练集精度:{}'.format(DTC.score(X_train,y_train)))
print('测试集精度:{}'.format(DTC.score(X_test,y_test)))
训练集精度:0.9741784037558685
测试集精度:0.9300699300699301
由于树深度很大,训练精度很高,但是测试精度较低,下面限制树深查看结果:
##使用乳腺癌数据集构造决策树
DTC =DecisionTreeClassifier(max_depth=3).fit(X_train,y_train)
print('训练集精度:{}'.format(DTC.score(X_train,y_train)))
print('测试集精度:{}'.format(DTC.score(X_test,y_test)))
训练集精度:0.9765258215962441
测试集精度:0.9440559440559441
分析决策树
from sklearn.tree import export_graphviz
export_graphviz(DTC,out_file='tree.dot',class_names=["malignant","benign"],feature_names=cancer.feature_names)
import graphviz
with open('tree.dot','r') as f:
dot_graph = f.read()
graphviz.Source(dot_graph)
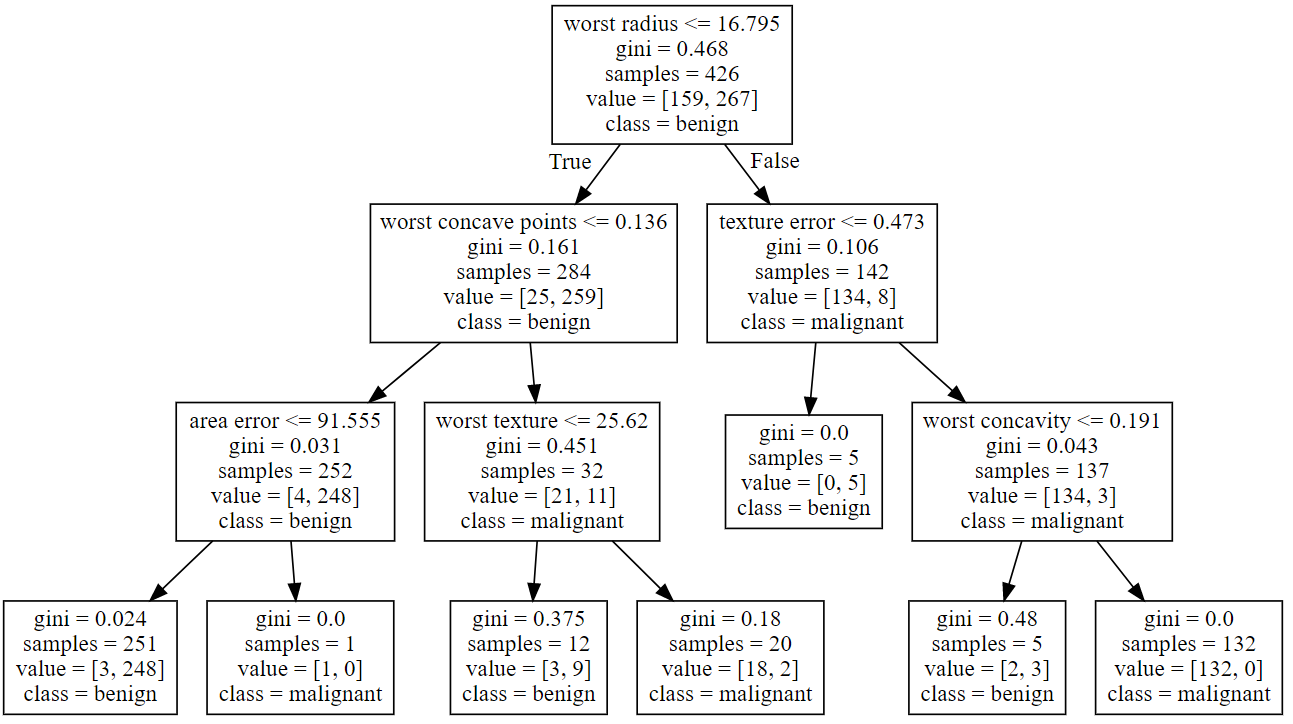
第一层,在根节点处,根据特征worst perimeter是否小于等于112.8将数据划分为两类,划分前基尼系数0.468,节点共426个样本,其中正负样本分别为159和267个,节点类别为benign。第二层为划分后数据,划分后基尼系数分别为0.161和0.106。按照样本量占比对其进行加权即可得出本层的总基尼系数,\(0.161\times(284\div426)+0.106\times(142\div426)=0.143\) 。可以看出基尼系数显著下降。
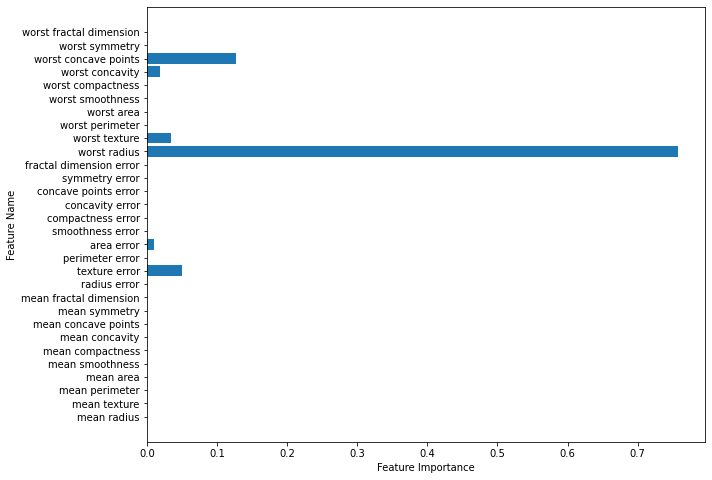
树的特征重要性
树的特征重要性可以使用tree.feature_importance_查看,特征重要性基于决策树的实现算法使用gini或者香农熵进行计算,特征重要性的和为1,且每个特征的重要性位于 [0,1] 之间。
如上图中,每次使用一个特征划分后,就会产生一个基尼系数的增量,以这个增量大小衡量特征的重要性,即求得所有特征对应的划分增量占总增量的比值,即为特征重要性。
具体的,还是以上图,以worst radius为例,之前求出在根节点处,使用该特征划划分后的基尼系数
然后计算完全划分后的所有叶节点的基尼系数(有三个叶节点是纯净的):
初始基尼系数为\(0.468\),worst radius的基尼系数增量就是:
总的基尼系数增量为
因此worst radius的特征重要性就是
DTC.feature_importances_
array([0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.0504697 , 0. , 0.01063382, 0. ,
0. , 0. , 0. , 0. , 0. ,
0.75793681, 0.03465357, 0. , 0. , 0. ,
0. , 0.01896644, 0.12733965, 0. , 0. ])
可以看出,与sklearn给出的结果基本相同,下面将特征重要性可视化:
def plot_feature_importance_cancer(model):
plt.subplots(figsize=(10,8))
plt.barh(range(cancer.data.shape[1]),model.feature_importances_)
plt.yticks(range(cancer.data.shape[1]),cancer.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Feature Name')
plot_feature_importance_cancer(DTC)
预测概率值
对于分类树,有一个方法是predict_prob可以给出每个样本被分为每个类别的概率,这个概率是使用每个叶节点中不同类别样本占比所得出的条件概率。如下所示,共有7个叶节点,因此共有七种不同的概率,其中最多的节点有251个样本,且被分类为benign。
在实际使用时,DTC.predict()方法使用默认的0.5作为阈值,我们可以根据实际情况,选用不同的阈值,从而调整预测的precision和recall。
pd.DataFrame(DTC.predict_proba(X_train)).value_counts()
0 1
0.015936 0.984064 251
0.992248 0.007752 129
0.941176 0.058824 17
0.444444 0.555556 9
0.142857 0.857143 7
0.857143 0.142857 7
0.000000 1.000000 6
dtype: int64
skearn参数说明
| 参数 | DecisionTreeClassifier | DecisionTreeRegressor |
|
criterion:特征选择标准 |
{“gini”, “entropy”}, default=”gini”,前者代表基尼系数,后者代表信息增益。一般说使用默认的基尼系数"gini"就可以,即CART算法。 |
{“squared_error”, “friedman_mse”, “absolute_error”, “poisson”}, default=”squared_error”。分别是“均方误差MSE”“friedmanMSE”“平均绝对误差MAE”“泊松偏差”,一般使用默认的"mse"。 |
|
splitter:特征划分点选择标准 |
可以使用"best"或者"random"。前者在特征的所有划分点中找出最优的划分点。后者是随机的在部分划分点中找局部最优的划分点。 比如在Cart离散变量特征最优选择的时候,因为要把所有的特征组合成两组,大概有$2^{n-1}$的数量级的循环遍历,计算量巨大。因此,默认的"best"适合样本量不大的时候,而如果样本数据量非常大,此时决策树构建推荐"random" |
|
|
max_features:划分时考虑的最大特征数 |
int, float or {“auto”, “sqrt”, “log2”}, default=None。可以使用很多种类型的值,默认是"None",和"auto"一样,意味着划分时考虑所有的特征数(分类树"auto"与"sqrt"一样);如果是"log2"意味着划分时最多考虑$log_2N$个特征;如果是"sqrt"或者意味着划分时最多考虑$\sqrt{N}$个特征。如果是整数,代表考虑的特征绝对数。如果是浮点数,代表考虑特征百分比,即考虑int(max_features * n_features)取整后的特征数。其中N为样本总特征数。 一般来说,如果样本特征数不多,比如小于50,我们用默认的"None"就可以了,如果特征数非常多,我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数,以控制决策树的生成时间。 |
|
|
max_depth:决策树最大深度 |
int, default=None。决策树的最大深度,默认可以不输入,如果不输入的话,决策树在建立子树的时候不会限制子树的深度。一般来说,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间。 | |
|
min_samples_split:内部节点再划分所需最小样本数 |
int or float, default=2。这个值限制了子树继续划分的条件,如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。如果输入为小于1的float,即百分比,则最小节点划分样本数为ceil(min_samples_leaf * n_samples) | |
|
min_samples_leaf:叶子节点最少样本数 |
int or float, default=1。这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数,或者最少样本数占样本总数的百分比,同样的,百分比表示的最小样本数为ceil(min_samples_leaf * n_samples) | |
|
min_weight_fraction_leaf:叶子节点最小的样本权重和 |
float, default=0.0。这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝。 默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。 | |
|
max_leaf_nodes:最大叶子节点数 |
int, default=None。通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制,具体的值可以通过交叉验证得到。 | |
|
class_weight:类别权重 |
dict, list of dict or “balanced”, default=None。指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多,导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重,或者用“balanced”,如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。当然,如果你的样本类别分布没有明显的偏倚,则可以不管这个参数,选择默认的"None" | 不适用于回归树 |
|
min_impurity_split:节点划分最小不纯度 |
float, default=0.0。这个值限制了决策树的增长,如果某节点的不纯度加权增量(基尼系数,信息增益,均方差,绝对差)小于这个阈值,则该节点不再生成子节点。即为叶子节点 。 | |



