Softmax：原理及python实现
Table of Contents
SoftMax回归概述
与逻辑回归类似，Softmax回归也是用于解决分类问题。不同的是，逻辑回归主要用于解决二分类问题，多分类问题需要通过OvO、MvM、OvR等策略来解决，softmax回归则是直接用于解决多分类问题。
标签编码
在二分类问题中，可以直接使用{0，1}来标注标签\(y\)，但是在多分类问题中，我们需要寻找其他的表示方法。对于类别，{婴儿,儿童,青少年,青年人,中年人,老年人} ，很自然的想到使用{1,2,3,4,5,6}来标注标签，对于这个例子当然是合适的，因为各个类别之间有明显的顺序关系，这也是有意义的。但是对于{铅笔，钢笔，签字笔}这个例子，直接使用带有顺序的数字标签是不合理的。因此，通常情况下，可以选择Onehot编码：
\[y \in \{(1, 0, 0), (0, 1, 0), (0, 0, 1)\}.
\]
算法思路
与逻辑回归类似，softmax也是基于线性回归，对于每一个样本，对每一个类别，预测出一个数值，然后使用softmax函数，将其转换成“概率”，然后在所有类别中，选择预测“概率”最大的值作为预测类别。
\[\vec{o_i} = W\vec{x_i}
\]
用非矩阵表示就是：
\begin{split}\begin{aligned}
o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1,\
o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2,\
o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3.
\end{aligned}\end{split}
用神经网络图可以更清晰的表示这个过程：
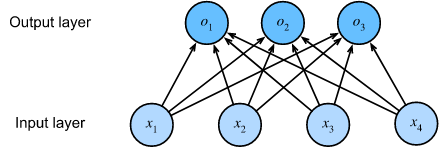
预测出的结果也就是向量\(\vec{o}\)，其元素值是在整个实数空间的，因此，使用softmax对其进行变换，使其转化为可以理解为概率的形式：
\[\hat{y_i} = Softmax(\vec{o_i}) \quad {其中}\quad \hat{y}_j = \frac{\exp(o_j)}{\sum\limits_{a=1}^k \exp(o_a)}\quad j = 1,2,3...k
\]
举个例子，比如\(\vec{o_i}={(1,2,3)}\)，则\(\hat{y_i}=(\frac e{e+e^2+e^3},\frac {e^2}{e+e^2+e^3},\frac {e^3}{e+e^2+e^3})\)，可以看出，向量\(\hat{y_i}\)的各元素和为1，因此可以理解为样本\(i\)被分类为三个类别所对应的概率，我们选择概率最大的类别作为最终的分类类别。
SoftMax的损失函数及其优化
损失函数
上一节介绍了Softmax的基本思路，现在要解决的问题就是如何通过计算获得参数矩阵\(W\)和参数向量\(\vec{b}\)。假设我们已经获取了样本容量为\(m\)，特征数为\(n\)的样本矩阵\(X_{m\times n}\)，以及对应的标签矩阵\(Y_{m\times k}\)，其中，分类类别数为\(k\)。与逻辑回归类似，由MLE可得损失函数为
\[L=\prod\limits_{i=1}^mP(\vec{y_i}|\vec{x_i})
\]
对数损失函数为
\[-lnL = \sum\limits_{i=1}^m-lnP(\vec{y_i}|\vec{x_i})=\sum\limits_{i=1}^ml(\vec{y_i},\hat {y}_i)
\]
其中
\[l(\vec y_i,\hat y_i)=-\vec y_i ln\hat y_i=-\sum\limits_{j=1}^k y_j^{(i)}ln(\hat y_j^{(i)})
\]
\(\vec y_i\)是第\(i\)个样本的\(label\)向量，\(\hat y_j^{(i)}\)是第\(i\)个样本的预测向量的第\(j\)项。
可以看出，对数损失函数中的条件概率其实是我们预测出的概率向量在对应的Onehot为1的位置的概率值，可以将其巧妙的表示为\(l(y_i,\hat y_i)\)的表达式。
损失函数的求导
对\(l(y_i,\hat y_i)\)做如下化简：
\[\begin{split}l(y_i,\hat y_i)&=-\sum\limits_{j=1}^k y_jln\frac{exp(o_j)}{\sum\limits_{a=1}^k exp(o_a)}\\ &=\sum\limits_{j=1}^k y_jln\frac{\sum\limits_{a=1}^k exp(o_a)}{exp(o_j)}\\ &=\sum\limits_{j=1}^k y_jln{\sum\limits_{a=1}^k exp(o_a)}-{\sum\limits_{j=1}^k y_jo_j}\\ &=ln{\sum\limits_{a=1}^k exp(o_a)}-{y_bo_b}\end{split}
\]
则有
\[\frac {\partial l(y_i,\hat y_i)}{\partial o_j}=\frac{exp(o_j)}{\sum\limits_{a=1}^kexp(o_a)}-y_j=Softmax(o_j)-y_j
\]
改写为向量形式就是
\[\frac {\partial l(y_i,\hat y_i)}{\partial \vec o_i}=Softmax(\vec o_i)-\vec y_i
\]
由于
\[dl_i = tr(\frac{\partial l_i}{\partial \vec o_i}^T d\vec o_i)= tr(\frac{\partial l_i}{\partial \vec o_i}^T dW\vec x_i)= tr((\frac{\partial l_i}{\partial \vec o_i}\vec x_i^T)^T dW)
\]
故
\[\frac{\partial l_i}{\partial W}=\frac{\partial l_i}{\partial \vec o_i}\vec x_i^T=[Softmax(W\vec x_i)-\vec y_i]x_i^T
\]
\[\frac {\partial (-lnL)}{\partial W}=\sum\limits_{i=1}^m[Softmax(W\vec x_i)-\vec y_i]x_i^T=[Softmax(WX^T)-y^T]X
\]
\[W=W-\alpha[Softmax(WX^T)-y^T]X
\]
其中
\[X=\begin{bmatrix} x_1^T \\ x_2^T \\...\\x_m^T\end{bmatrix},y=\begin{bmatrix} y_1^T \\ y_2^T\\ ...\\y_m^T\end{bmatrix}
\]
\(x_i,y_i均为列向量\)
Softmax实现
图片数据集
这里使用李沐老师课程里用到的图片数据集。
import matplotlib.pyplot as plt
%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
import warnings
warnings.filterwarnings('ignore')
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="./data", train=True,
transform=trans,
download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="./data", train=False,
transform=trans, download=True)
下载完成数据集后，可以看出训练集中有60000条数据，mnist_train[0]可以获取第一张图片的信息，它包含两项，第一项是图片的矩阵数据，是一个[1,28,28]的矩阵，第二项是label标签，可以使用plt.imshow来查看图片。
len(mnist_train)
60000
len(mnist_train[0])
2
mnist_train[0][0].shape
torch.Size([1, 28, 28])
mnist_train[0][1]
9
plt.imshow(mnist_train[0][0][0])
plt.show()
sklearn实现
sklearn中LogisticsRegression类中，参数multi_class设置为multinomial时，使用的就是softmax回归。
from sklearn.linear_model import LogisticRegression
# 数据获取
X_train,y_train = next(iter(data.DataLoader(mnist_train,batch_size=len(mnist_train))))
X_train = X_train.reshape((len(mnist_train),-1))
X_test,y_test = next(iter(data.DataLoader(mnist_test,batch_size=len(mnist_test))))
X_test = X_test.reshape((len(mnist_test),-1))
# 模型训练
soft_sk = LogisticRegression(multi_class='multinomial').fit(X_train.numpy(),y_train.numpy())
# 评分
soft_sk.score(X_train,y_train),soft_sk.score(X_test,y_test)
(0.8659833333333333, 0.8438)
python从零实现
使用梯度下降按照第二节中的方法优化参数，由于涉及计算Softmax很容易溢出，因此设置了很小的学习率。但是，性能一直无法优化到80%，希望有大佬指教一下。
import numpy as np
from torch.utils import data
import random
from torchvision import transforms
import torchvision
import pandas as pd
class Softmax:
def __init__(self, X, y, batch_size=5, epoch=3, alpha=0.00001):
self.features = np.array(np.insert(X, 0, 1, axis=1))
self.labels_original = y
self.labels = pd.get_dummies(self.labels_original).values
self.batch = batch_size
self.epoch = epoch
self.alpha = alpha
self.n_class = len(y.unique())
self.n_features = self.features.shape[1]
self.W = np.random.normal(0, 0.01, (self.n_class, self.n_features))
def softmax(self, X):
X = np.array(X)
X = X - X.max()
return np.exp(X)/np.sum(np.exp(X), axis=1, keepdims=True)
def data_iter(self):
range_list = np.arange(self.features.shape[0])
random.shuffle(range_list)
for i in range(0, len(range_list), self.batch):
batch_indices = range_list[i:min(i + self.batch, len(range_list))]
yield self.features[batch_indices], self.labels[batch_indices]
def fit(self):
for i in range(self.epoch):
for X, y in self.data_iter():
self.W -= self.alpha * np.matmul((self.softmax(np.matmul(self.W, X.T))-y.T), X)
def predict(self, X_pre):
X_pre = np.array(np.insert(X_pre, 0, 1, axis=1))
return np.argmax(self.softmax(np.matmul(self.W, X_pre.T)), axis=0)
def score(self, y_true, y_pre):
return np.sum(np.ravel(y_true) == np.ravel(y_pre))/len(y_true)
def main():
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="./data", train=True,
transform=trans,
download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="./data", train=False,
transform=trans, download=True)
X_train, y_train = next(iter(data.DataLoader(mnist_train, batch_size=len(mnist_train))))
X_train = X_train.reshape((len(mnist_train), -1))
X_test, y_test = next(iter(data.DataLoader(mnist_test, batch_size=len(mnist_test))))
X_test = X_test.reshape((len(mnist_test), -1))
soft_max = Softmax(X_train, y_train)
soft_max.fit()
y_train_pre = soft_max.predict(X_train)
y_test_pre = soft_max.predict(X_test)
print(f"训练集准确度：{soft_max.score(y_train,y_train_pre)}")
print(f"测试集准确度：{soft_max.score(y_test, y_test_pre)}")
if __name__ == '__main__':
main()
训练集准确度：0.6503333333333333
测试集准确度：0.6419
使用pytorch的实现
import torch
import torchvision
from torch.utils import data
from torch import nn
from torchvision import transforms
class SoftmaxPytorch:
def __init__(self, X, y, batch_size=256, epoch=5, lr=0.1):
self.features = torch.tensor(X)
self.labels = torch.tensor(y).reshape(-1, 1)
self.batch = batch_size
self.epoch = epoch
self.lr = lr
self.n_features = self.features.shape[1]
self.n_class = len(self.labels.unique())
self.loss = nn.CrossEntropyLoss()
self.net = nn.Sequential(nn.Flatten(), nn.Linear(self.n_features, self.n_class))
self.trainer = torch.optim.SGD(self.net.parameters(), self.lr)
def data_iter(self):
dataset = data.TensorDataset(self.features, self.labels)
return data.DataLoader(dataset, self.batch, shuffle=True)
def init_weights(self, model):
if type(model) == nn.Linear:
nn.init.normal_(model.weight, std=0.01)
def fit(self):
self.net.apply(self.init_weights)
for i in range(self.epoch):
for X, y in self.data_iter():
y_hat = self.net(X)
l = self.loss(y_hat, y.ravel())
self.trainer.zero_grad()
l.sum().backward()
self.trainer.step()
print(f'epoch:{i},loss:{self.loss(self.net(self.features), self.labels.ravel())}')
def predict(self, X_pre):
y_hat = self.net(X_pre)
y_pre = torch.argmax(y_hat, axis=1)
return y_pre
def score(self, y_hat, y_true):
return sum(y_hat.type(y_true.dtype).ravel() == y_true.ravel())/len(y_true)
def main():
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="./data", train=True,
transform=trans,
download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="./data", train=False,
transform=trans, download=True)
X_train, y_train = next(iter(data.DataLoader(mnist_train, batch_size=len(mnist_train))))
X_train = X_train.reshape((len(mnist_train), -1))
X_test, y_test = next(iter(data.DataLoader(mnist_test, batch_size=len(mnist_test))))
X_test = X_test.reshape((len(mnist_test), -1))
sf = SoftmaxPytorch(X_train, y_train)
sf.fit()
y_train_pre = sf.predict(X_train)
train_score = sf.score(y_train_pre, y_train)
y_test_pre = sf.predict(X_test)
test_score = sf.score(y_test_pre, y_test)
print(f'训练集准确率：{train_score}')
print(f'测试集准确率：{test_score}')
if __name__ == '__main__':
main()
epoch:0,loss:0.6310750842094421
epoch:1,loss:0.5460468530654907
epoch:2,loss:0.5175894498825073
epoch:3,loss:0.49569806456565857
epoch:4,loss:0.473165899515152
训练集准确率：0.84211665391922
测试集准确率：0.8271999955177307
