线性回归：原理及python实现
目录
# 线性回归概述
什么是线性回归呢？
回归问题的一般模型如下：
\[y = \sum w[i]*x[i]+b
\]
如下图所示，对于一维数据，线性回归就是根据给定的点\((x_i,y_i)\)拟合出一条直线
\[y=ax+b
\]
即求出系数a、b。
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import mglearn
mglearn.plots.plot_linear_regression_wave()
w[0]: 0.393906 b: -0.031804
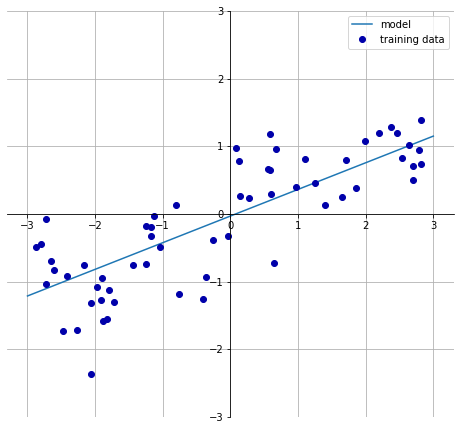
推广到多维数据，线性回归模型的训练过程就是寻找参数向量w的过程，只是拟合的目标变为了高维平面，线性回归最常用的两种方法是最小二乘法（OLS）和梯度下降法。
求解方法
普通最小二乘法（Ordinary Least Square，OLS）
一元线性回归的最小二乘
最小二乘法基于这样一个目标，使得数据的实际值 \(y_i\) 与预测值 \(\hat{y_i}\)之间的偏差最小，即损失函数，OLS使用均方误差（Mean Square Error，MSE）作为损失函数，优化目标为
\[min\quad MSE=\frac 1n\sum_{i=1}^n(y_i-\hat{y_i})^2
\]
对于一维数据而言
\[MSE=\frac 1n\sum_{i=1}^n(y_i-\theta_0-\theta_1x_i)^2
\]
为求最小值，需要求偏导
\[\frac {\partial MSE}{\partial\theta_0}=-\frac 2n\sum_{i=1}^n(y_i-\theta_0-\theta_1x_i)=0
\]
\[\frac {\partial MSE}{\partial\theta_1}=-\frac 2n\sum_{i=1}^n(y_i-\theta_0-\theta_1x_i)x_i=0
\]
联立可得
\[\theta_1=\frac {\sum(y_i-\bar y)(x_i-\bar x)}{(x_i-\bar x)^2}
\]
\[\theta_0=\bar y -\theta_1 \bar x
\]
多元线性回归的最小二乘
对于多元回归同理，下面是矩阵解法,损失函数定义为
\[J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y})
\]
求导
\[\frac{\partial}{\partial\mathbf\theta}J(\mathbf\theta) = \mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y}) = 0
\]
\[X^TX\theta-X^TY=0
\]
最终可得
\[\mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y}
\]
最小二乘法的局限
-
最小二乘法需要计算\(X^TX\)的逆矩阵，有可能它的逆矩阵不存在，这样就没有办法直接用最小二乘法了，此时梯度下降法仍然可以使用。当然，可以通过对样本数据进行整理，去掉冗余特征,让\(X^TX\)的行列式不为0，然后继续使用最小二乘法。
-
当样本特征n非常的大的时候，计算\(X^TX\)的逆矩阵是一个非常耗时的工作（\(n\times n\)的矩阵求逆），甚至不可行。此时以梯度下降为代表的迭代法仍然可以使用。如果没有很多的分布式大数据计算资源，建议超过10000个特征就用迭代法。或者通过主成分分析降低特征的维度后再用最小二乘法。
-
如果拟合函数不是线性的，这时无法使用最小二乘法，需要通过一些技巧转化为线性才能使用，此时梯度下降仍然可以用。
-
当样本量m很少，小于特征数n的时候，这时拟合方程是欠定的，常用的优化方法都无法去拟合数据。当样本量m等于特征数n的时候，用方程组求解就可以了。当m大于n时，拟合方程是超定的，也就是我们常用与最小二乘法的场景了。
梯度下降（Gradient Decent，GD）
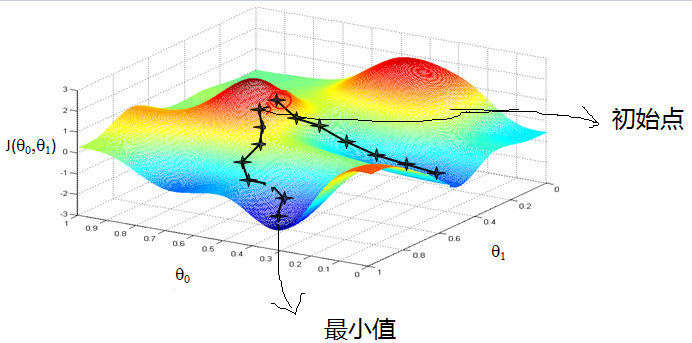
梯度下降法是一个比较纯粹的计算机编程方法。
如图所示，我们知道，损失函数是系数的函数，一元线性回归有两个参数，组成了损失函数平面，我们首先随机指定一组系数，即在上图平面上随机选取一个初始点，然后同时进行以下变换
\[\theta_0 = \theta_0-\alpha\frac{\partial J(\theta)}{\partial \theta_0}
\]
\[\theta_1 = \theta_1-\alpha\frac{\partial J(\theta)}{\partial \theta_1}
\]
重复该步骤直到终止。
我们来分析一下发生了什么。首先，偏导数的系数\(\alpha\)是正数。对于偏导数而言，当偏导大于零的时候，\(J(\theta)\)随\(\theta_i\)增大而增大，同时，新的\(\theta_i\)小于旧的\(\theta_i\)，因此，\(J(\theta)\)减小；当偏导数小于零的时候，\(J(\theta)\)随着\(\theta_i\)增大而减小，同时，新的\(\theta_i\)大于旧的\(\theta_i\)，因此，\(J(\theta)\)还是减小，即每次循环，损失函数都会减小，最终到达一个局部的最小值，即极小值。
但是，我们的损失函数是凸函数，并不是有多个极小值的图形，其真实图形如下所示，极小值即为最小值。
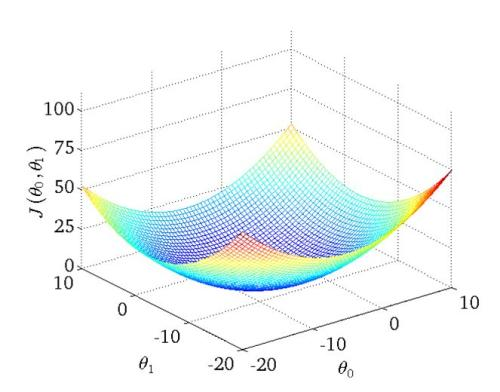
线性回归的实现
sklearn实现
skearn作为广为使用的机器学习包，可以简单的实现线性回归。sklearn中使用OLS拟合模型，score是可决系数，可以看出，测试集可决系数只有0.65左右，可以说效果并不好，这是因为原数据为一维数据，当数据维度增加时，线性模型可以变得十分强大。
#使用sklearn进行线性回归
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X,y = mglearn.datasets.make_wave(n_samples=60) #导入数据
print("数据集的第一个样本点：X:{}y:{}".format(X[0],y[0]))
#数据集划分，同一random_state表示对数据集进行相同的划分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=42)
#标准的sklearn风格API，Model（）.fit（X,y）
lr = LinearRegression().fit(X_train,y_train)
print('系数:{}'.format(lr.coef_))
print('截距：{}'.format(lr.intercept_))
print('训练精度：{}'.format(lr.score(X_train,y_train)))
print('测试精度：{}'.format(lr.score(X_test,y_test)))
数据集的第一个样本点：X:[-0.75275929]y:-1.1807331091906834
系数:[0.39390555]
截距：-0.031804343026759746
训练精度：0.6700890315075756
测试精度：0.65933685968637
statsmodels实现
statsmodels是一个统计方面的包，是对scipy.stats的补充，主要是回归预测方面的功能加强。
import statsmodels.api as sm
#给模型添加常数项，如果不执行，则训练出的直线过原点
x = sm.add_constant(X_train)
print("添加常数后数据：\n%s" % x[0:5])
#训练模型
ols = sm.OLS(y_train,x).fit()
#输出统计报告
print(ols.summary())
添加常数后数据：
[[ 1. 0.14853859]
[ 1. 0.60669007]
[ 1. -2.65149833]
[ 1. -2.26777059]
[ 1. -2.06388816]]
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.670
Model: OLS Adj. R-squared: 0.662
Method: Least Squares F-statistic: 87.34
Date: Sun, 26 Sep 2021 Prob (F-statistic): 6.46e-12
Time: 11:10:30 Log-Likelihood: -33.187
No. Observations: 45 AIC: 70.37
Df Residuals: 43 BIC: 73.99
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0318 0.078 -0.407 0.686 -0.190 0.126
x1 0.3939 0.042 9.345 0.000 0.309 0.479
==============================================================================
Omnibus: 0.703 Durbin-Watson: 2.369
Prob(Omnibus): 0.704 Jarque-Bera (JB): 0.740
Skew: -0.081 Prob(JB): 0.691
Kurtosis: 2.393 Cond. No. 1.90
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
summary输出的是一张类似eviews或者minitab统计风格的表，可以看到，可决系数R-squared是0.67，与sklearn结果相同，并且，模型的F-statistic以及参数的t检验都表明，结果是显著的。
python从零实现
下面使用python使用小批量梯度下降法来实现线性回归，首先定义了一个LinearRegression类。在main中，首先，创建了一个模拟数据集，数据集\(weitht = [1,2]\),\(bias=4\)。然后，实例化了一个线性回归对象，传入训练数据，然后调用fit方法，使用梯度下降优化参数。最终输出\(weith=[1.0010,1.9993]\),\(bias=3.9998\)
在LinearRegression类中，data_iter函数每次调用返回一个大小为batch_size的样本集，MSE_loss用于计算均方误差损失，gradient_decent用于更新参数，在gradient_decent中，这里使用了pytorch的自动求导来计算导数。这里对数据集迭代epoch次，每次将全部数据集划分为多个小批量更新参数。
import random
import torch
class LinearReg:
def __init__(self, X, y, batch_size=10, epoch=20, learning_rate=0.01):
self.X = X
self.y = y
self.w = torch.normal(0, 1, (self.X.shape[1], 1), requires_grad=True)
self.b = torch.zeros(1, requires_grad=True)
self.batch_size = batch_size
self.epoch = epoch
self.learning_rate = learning_rate
def data_iter(self):
indices = list(range(len(self.X)))
random.shuffle(indices)
for i in range(0, len(self.X), self.batch_size):
batch_indices = indices[i:min(i + self.batch_size, len(self.X))]
yield self.X[batch_indices], self.y[batch_indices]
def MSE_loss(self, y_true, y_pre):
return torch.mean((y_true-y_pre.reshape(y_true.shape))**2)/2
def linearReg(self, X):
return torch.matmul(X, self.w) + self.b
def gradient_decent(self, params):
with torch.no_grad():
for param in params:
param -= self.learning_rate * param.grad
param.grad.zero_()
def fit(self):
for i in range(self.epoch):
for X_batch, y_batch in self.data_iter():
y_pre = self.linearReg(X_batch)
l = self.MSE_loss(y_batch, y_pre)
l.backward()
self.gradient_decent([self.w, self.b])
# print(f'{i}:{float(self.MSE_loss(y, LinearRegression(self.X, self.w, self.b)))}')
def predict(self,X_pre):
return self.LinearRegression(X_pre)
def parameter(self):
return [self.w, self.b]
def creat_dataset(w, b, num_sample):
X = torch.normal(0, 1, (num_sample, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape((-1, 1))
def main():
X, y = creat_dataset(torch.tensor([1., 2]), 4, 1000)
lr = LinearReg(X, y)
lr.fit()
print(lr.parameter())
if __name__ == '__main__':
main()
[tensor([[0.9994],
[2.0000]], requires_grad=True), tensor([4.0000], requires_grad=True)]
线性回归的简洁实现
这里与上一节比较类似，但是大量使用了pytorch的API来减少代码量。
from d2l import torch as d2l
import torch
from torch.utils import data
from torch import nn
class linearReg:
def __init__(self, X, y, batch=10, learning_rate=0.03, epochs=3):
self.features = X
self.lalels = y
self.batch = batch
self.learning_rate = learning_rate
self.epochs = epochs
self.net = nn.Sequential(nn.Linear(self.features.shape[1], 1))
self.loss = nn.MSELoss()
def data_iter(self, shuffle=True):
dataset = data.TensorDataset(self.features, self.lalels)
return data.DataLoader(dataset, self.batch, shuffle=shuffle)
def fit(self):
self.net[0].weight.data.fill_(0)
self.net[0].bias.data.fill_(0)
trainer = torch.optim.SGD(self.net.parameters(), lr=self.learning_rate)
for epoch in range(self.epochs):
for features, labels in self.data_iter():
l = self.loss(self.net(features), labels)
trainer.zero_grad()
l.backward()
trainer.step()
l = self.loss(self.net(self.features), self.lalels)
print(f'epoch:{epoch+1},loss:{l:f}')
def print_param(self):
print(f'weight:{self.net[0].weight.data}')
print(f'bias:{self.net[0].bias.data}')
def main():
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
linearR = linearReg(features, labels)
linearR.fit()
linearR.print_param()
if __name__ == '__main__':
main()
epoch:1,loss:0.000222
epoch:2,loss:0.000092
epoch:3,loss:0.000092
weight:tensor([[ 2.0013, -3.3999]])
bias:tensor([4.1996])
线性回归的推广
多项式回归
对于一元线性回归，当因变量y与x并不成线性关系时，无法直接使用线性回归。根据泰勒定理：
\[f(x) = \frac{f^{(0)}(a)}{0!}+\frac{f^{(1)}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+...+\frac{f^{(n)}(a)}{n!}(x-a)^n+R_n(x)
\]
令a=0可知，y可以由\(x,x^2,x^3...\)线性表示，因此，可以将\(x^n\)看作额外的变量，将一元线性回归转化为多元线性回归，以此来增加模型的准确性。
df = pd.DataFrame(X_train)
df[1] = df[0]*df[0]
df[2] = df[0]*df[1]
X_train = df.values
x = sm.add_constant(X_train)
ols = sm.OLS(y_train,x).fit()
print(ols.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.708
Model: OLS Adj. R-squared: 0.686
Method: Least Squares F-statistic: 33.10
Date: Sun, 26 Sep 2021 Prob (F-statistic): 4.93e-11
Time: 11:20:05 Log-Likelihood: -30.459
No. Observations: 45 AIC: 68.92
Df Residuals: 41 BIC: 76.15
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0942 0.119 -0.795 0.431 -0.334 0.145
x1 0.6298 0.116 5.433 0.000 0.396 0.864
x2 0.0186 0.027 0.686 0.497 -0.036 0.073
x3 -0.0408 0.019 -2.133 0.039 -0.079 -0.002
==============================================================================
Omnibus: 0.536 Durbin-Watson: 2.475
Prob(Omnibus): 0.765 Jarque-Bera (JB): 0.668
Skew: -0.150 Prob(JB): 0.716
Kurtosis: 2.484 Cond. No. 18.9
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
可以看出，添加x的二次方和三次方项后，可决系数有所提升，但是二次方项系数t检验不显著，后续可以考虑去除。
对数线性回归
即通过取对数将原本无线性关系的变量转化为近似线性关系以应用线性回归，如对数线性回归：
\[ln\mathbf{Y} = \mathbf{X\theta}
\]
更一般的,
\[y = g^{-1}(\mathbf{X\theta})
\]
或
\[g(y)=\mathbf{X\theta}
\]
这类线性回归的推广应用统称广义线性回归。
线性回归的正则化
岭回归
岭回归使用L2正则化处理回归模型，其惩罚项为L2范数，惩罚项系数为正数，对应sklearn.Ridge中参数alpha，增大alpha会导致系数趋向于0，从而降低训练集性能，是解决过拟合的一种方法，同样的，sklearn.ridge使用OLS。
\[J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \frac{1}{2}\alpha||\theta||_2^2
\]
\[\frac{\partial}{\partial\mathbf\theta}J(\mathbf\theta) = \mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y}) +\alpha\theta= 0
\]
\[\theta = (X^TX + \alpha E)^{-1}X^TY
\]
#岭回归在sklearn中的实现
from sklearn.linear_model import Ridge
X,y = mglearn.datasets.load_extended_boston()
print('数据规模：{}'.format(X.shape))
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state = 0)
ridge = Ridge(alpha=1).fit(X_train,y_train)
LR = LinearRegression().fit(X_train,y_train)
print('线性回归精度（[训练，测试]）：{}'.format([LR.score(X_train,y_train),LR.score(X_test,y_test)]))
print('岭回归精度（[训练，测试]）：{}'.format([ridge.score(X_train,y_train),ridge.score(X_test,y_test)]))
数据规模：(506, 104)
线性回归精度（[训练，测试]）：[0.9520519609032727, 0.6074721959665571]
岭回归精度（[训练，测试]）：[0.8857966585170942, 0.7527683481744757]
lasso
lasso使用L1正则化，惩罚项是L1范数，但是可以使某特征系数为0，模型更容易解释，也可以呈现模型的重要特征，由于使用绝对值，存在不可导点，因此OLS、梯度下降都不可用。
\[J(\mathbf\theta) = \frac{1}{2m}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha||\theta||_1
\]
#lasso实现
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.01,max_iter=1000000).fit(X_train,y_train)
print('训练精度：{}'.format(lasso.score(X_train,y_train)))
print('测试精度：{}'.format(lasso.score(X_test,y_test)))
print('模型所用特征数：{}'.format(np.sum(lasso.coef_ !=0)))
训练精度：0.8962226511086497
测试精度：0.7656571174549982
模型所用特征数：33
ElasticNet
ElasticNet同时使用L1、L2范数进行正则化，
\[J(\mathbf\theta) = \frac{1}{2m}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha\rho||\theta||_1 + \frac{\alpha(1-\rho)}{2}||\theta||_2^2
\]
from sklearn.linear_model import ElasticNet
els = ElasticNet(alpha=0.01,l1_ratio=0.01).fit(X_train,y_train)
print('训练精度：{}'.format(els.score(X_train,y_train)))
print('测试精度：{}'.format(els.score(X_test,y_test)))
print('模型所用特征数：{}'.format(np.sum(els.coef_ !=0)))
训练精度：0.8354145388874659
测试精度：0.6975709513785231
模型所用特征数：102
