FSA/FSM/FST
有限状态机 Finite state machine 可以用来紧密的存储有序集合和有序键值对，并实现快速搜索
怎样用FSM来作为数据结构存储这样的数据？
什么是有序集合？
有序集合中的键按照字典顺序排序，典型的应用是BST/BTREE
什么是无序集合？
典型的应用是HashTable
确定无环有限状态接收器 FSA (deterministic acyclic finite state acceptor)
一个FSA需要满足以下条件：
• 确定性的。给定已给输入，最多只能转移到一个状态。
• 无环的。不能反序遍历。
• 接收器。FSA可以接收一系列特定的输入。
给定一个输入key，我们可以知道这个key这个key是否在FSA中
一个集合，只有一个key”jul”
FSA就像下面这样：
FSA是否包含”jul”
处理顺序如下：
• 给定j，FSA状态从0变为1.
• 给定u，FSA状态从1变为2.
• 给定l，FSA状态从2变为3.
输入结束，这时候判断一下FSA是否处在final状态(图中用双圈表示)，表明jul确实在set中。
FSA是否包含”ju”
处理顺序如下：
• 给定j，FSA状态从0变为1.
• 给定u，FSA状态从1变为2.
输入结束，判断一下，此时是否处于final状态
判断一个key是否存在，受限于key的长度，而不是set的大小。
复杂的FSA，包含三个key，october，november，december
因为有相同的后缀ber，在FSA中只需要编码一次就行了。两个key有更大的相同的后缀，ember。
如何来遍历FSA中所有的key呢？
用一个简单的图，有三个key，jul，jun和mar。
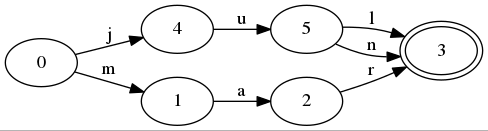
遍历方式如下：
• 初始化状态0
• 移动到状态4，把j添加到key中
• 移动到状态5，把u添加到key中
• 移动到状态3，把l添加到key中，输出jul
• 返回状态5，把key中的l抛弃掉
• 移动到状态3，把n添加到key中，输出jun
• 返回状态5，把key中的n抛弃掉
• 返回状态4，把key中的u抛弃掉
• 返回状态0，把key中的j抛弃掉
• 移动到状态1，把m添加到key中
• 移动到状态2，把a添加到key中
• 移动到状态3，把r添加到key中，输出mar
这个算法直接应用一个栈存储访问过的状态，和一个栈存储相应的转移。时间复杂度为O(n)，空间复杂度O(k)，k是set中最长的键的大小。
什么是有序Map？
他和有序集合类似，只是多了一个输出
有序map常用在BST/BTREE
无序map常用在hashTable
FST （deterministic acyclic finite state transducer）确定无环有限状态转移器
FST满足以下特性：
• 确定性。
• 无环。
• 一个转移器。给定一系列输入，会输出一个值。当且仅当输入会达到FST的final状态。
FST和FSA什么区别？
给定一个key
FSA告诉你是否包含该值
FST不仅告诉你是否包含该值，还会返回和这个key相关的一个Value。
FST怎么实现返回值的？
一种方法是，在每次转移的时候添加一些值。当输入序列在状态之间转移的时候，输出序列也在慢慢增加。
Eg:map中只包含一个数据jul，对应的value为7:
如果要判断，FST中是否存在key”jul”，并且需要对应的返回值，处理过程如下：
• 初始化value为0
• 给定输入j,FST从状态0转移到1，value+7
• 给定输入u，FST从状态1转移到2，value+0
• 给定输入l，FST从状态2转移到3，value+0
输入结束，状态3为final状态，因此key存在，value为7
下面把k-v,”mar 3”添加到FST中
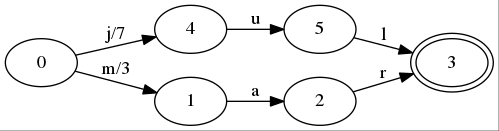
在起始节点，多了一个新的转移m，对应输出为3.如果我们查询jul，那么应该和上面是一样的处理过程。
继续，当添加一个有相同前缀的key，会发生什么呢？
添加key jun，value 6
在状态5和状态3之间添加了一个转移n。但是还有另外两个变化
- 0->4转移j输入对应输出从7变成了6.
- 5->3转移l输入对应输出从0变成了1.
这个变化之后们可以正确查询jun和jul，并且返回正确的值。
这种key的属性确保了，即使共享前缀，对于每一个key，然后只有一个唯一的路径可以贯穿整个machine。因此，每个key也有唯一的value。我们要做的就是怎么把这些输出放在转移中去。
其实不仅可以共享前缀，还可以共享后缀。对于两个key tuesday和thursday，分别对于输出3和5.
这两个key有相同的前缀t，相同的后缀sday，按照图里的方式可以保证输出的正确性。
Trie树构建
trie树，前缀树…..
