梯度下降的直线拟合
梯度下降的直线拟合#
实现说明#
给定若干个\(x, y\)并且求得一个最佳的\(y = ax + b\),也就是二元一次方程组的解。
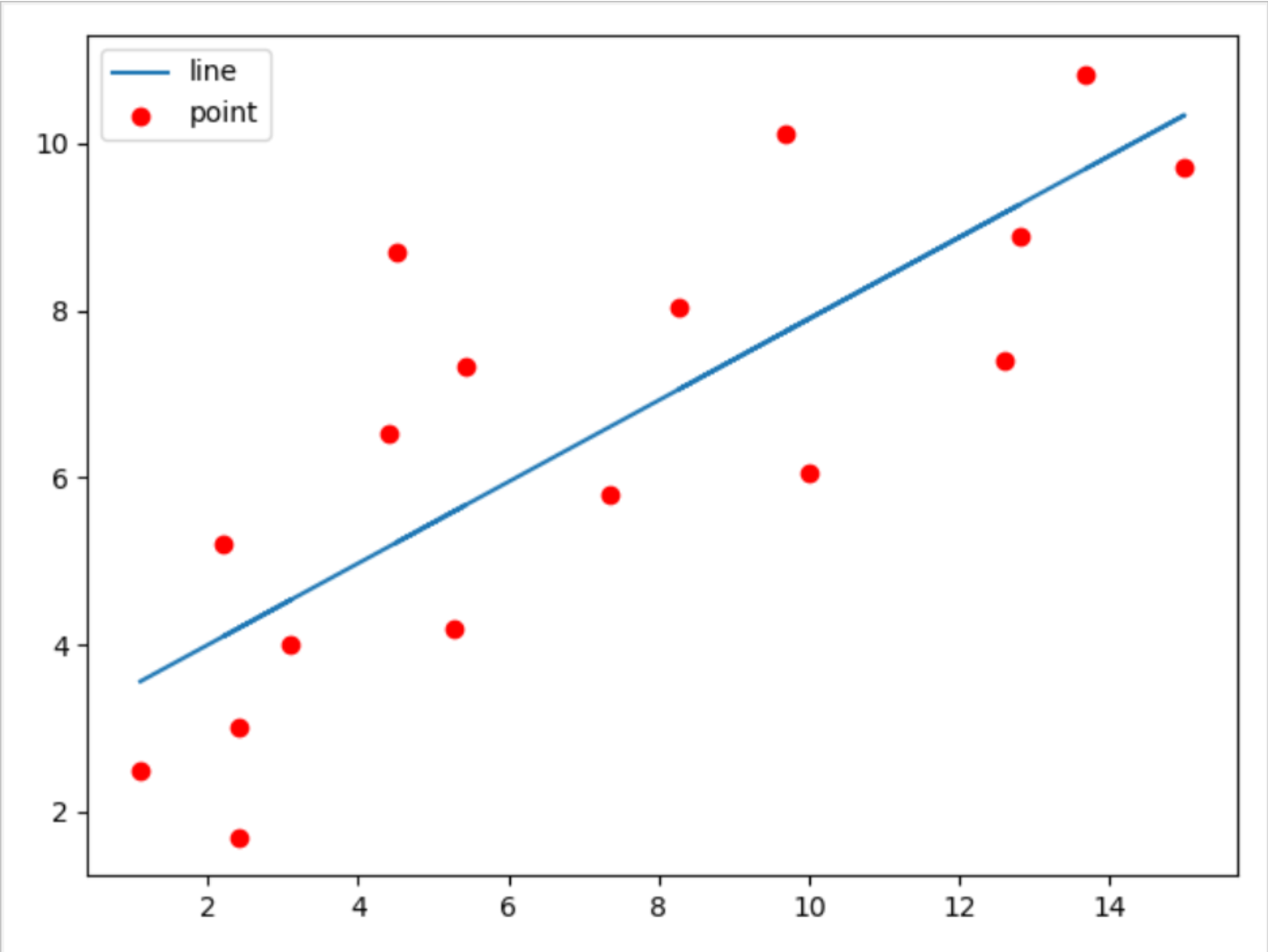
先放上给定的散点,以及求得的线性回归的直线的图片。
我个人认为,这里的梯度优化,就是通过一个关键式子\(loss = \sum(ax + b - y) ^{2}\),通过求解这个凹函数来得到他的最小值从而实现整个线性回归方程的最优解,具体的实现就如下分析。
\(\frac{\partial{loss}}{\partial{a}} = 2x(ax + b - y)\)
\(\frac{\partial{loss}}{\partial{b}} = 2(ax + b - y)\)
由此我们每次梯度下降更新的\(a = a - \frac{\partial{loss}}{\partial{a}} * learning\_rate\)
同样的每次梯度下降更新的\(b = b - \frac{\partial{loss}}{\partial{b}} * learning\_rate\)
然后通过这个迭代更新去得到最优损失的\(loss\),同时\(a, b\),也会在这个时候更新为最优值
PY‘S CODE#
import torch
import numpy as np
import matplotlib.pyplot as plt
x1 = np.array([1.1, 2.4, 2.4, 3.1, 2.2, 4.42, 5.43, 4.5, 5.28, 7.35, 10, 8.27, 12.6, 12.8, 9.69, 15.0, 13.69])
y1 = np.array([2.5, 1.7, 3, 4.0, 5.2, 6.53, 7.33, 8.7, 4.2, 5.8, 6.05, 8.05, 7.41, 8.89, 10.12, 9.72, 10.83])
def calc_error(a, b, data):
sum = 0
for i in range(len(data)):
x, y = data[i][0], data[i][1]
sum += (a * x + b - y) ** 2
return sum / (float)(len(data))
def gradient_step(now_a, now_b, data, learning_rate):
gradient_a, gradient_b = 0, 0
for i in range(len(data)):
x, y = data[i][0], data[i][1]
gradient_a += 2 * x * (now_a * x + now_b - y)
gradient_b += 2 * (now_a * x + now_b - y)
gradient_a /= len(data)
gradient_b /= len(data)
new_a = now_a - learning_rate * gradient_a
new_b = now_b - learning_rate * gradient_b
return [new_a, new_b]
def algorithm(start_a, start_b, data, learning_rate, iterator_num):
a, b = start_a, start_b
for i in range(iterator_num):
a, b = gradient_step(a, b, data, learning_rate)
return [a, b]
def run():
# 1.1, 2.4, 2.4, 3.1, 2.2, 4.42, 5.43, 4.5, 5.28, 7.35, 10, 8.27, 12.6, 12.8, 9.69, 15.0, 13.69
# 2.5, 1.7, 3, 4.0, 5.2, 6.53, 7.33, 8.7, 4.2, 5.8, 6.05, 8.05, 7.41, 8.89, 10.12, 9.72, 10.83
data = np.array([[1.100000, 2.500000], [2.400000, 1.700000], [2.400000, 3.000000],
[3.100000, 4.000000], [2.200000, 5.200000], [4.420000, 6.530000],
[5.430000, 7.330000], [4.500000, 8.700000], [5.280000, 4.200000],
[7.350000, 5.800000], [10.000000, 6.050000], [8.270000, 8.050000],
[12.600000, 7.410000], [12.800000, 8.890000], [9.690000, 10.120000],
[15.000000, 9.720000], [13.690000, 10.830000]])
a, b = 0, 0
# for i in range(1, 6):#通过改变迭代次数,对比其答案,
# iterator_num = 10 ** i
# print("iterator_num is {0}".format(iterator_num))
# print("befor a:{0}, b:{1}, error{2}".format(a, b, calc_error(a, b, data)))
# a, b = algorithm(a, b, data, 0.0001, iterator_num)
# print("after a:{0}, b:{1}, error{2}".format(a, b, calc_error(a, b, data)))
# print("")
a, b = algorithm(a, b, data, 0.001, 100000)#选了一个稍优的迭代次数,
print("My's {0}, {1} Standard's {2}, {3}".format(a, b, 0.487713, 3.0308))
print("")
# for i in range(len(data)):
# print("Data's y : {0} My's y : {1} Standard's y : {2}".format(data[i][1], a * data[i][0] + b, 0.487713 * data[i][0] + 3.0308))
# print("")
return [a, b]
if __name__ == "__main__":
plt.scatter(x1, y1, color = "red", label = "point")
a, b = run()
x = x1
y = a * x + b
plt.plot(x, y, label = "line")
plt.legend(loc = "best")
plt.show()
# print("heloo, word")


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步