求解逆元的三种方法

为什么要有逆元

我们知道 \((512 / 8) % 13 = 64 % 13 = 12\)，显然他是不遵循 \((512 \% 13) / (8 \% 13)\) 的，因此这里就要用到逆元了。
逆元的定义 \(a * b \equiv 1 (mod\ p)\)，a，p互质 b 就是 a 的逆元。
同时有 \(a * b + p * c \equiv 1 (mod\ p)\)

拓展欧几里德求逆元

这个过程也就似乎求解方程 \(a * x + b * y = 1\) 的过程， 但是有一个要注意的就是要保证最后求得的 x 是要大于0的，
也就是要对最后求得的 x 进行 x = (x % b + b) % b 一步操作。

代码

/*
    Code by lifehappy 2020:04:23
*/
#include<iostream>
using namespace std;
int exgcd(int a, int b, int &x, int &y) {
    if(!b) {
        x = 1;
        y = 0;
        return a;
    }
    int gcd = exgcd(b, a % b, x, y);
    int t = x;
    x = y;
    y = t - a / b * y;
    return gcd;
}
int main() {
    int a, b, x, y;
    while(cin >> a >> b) {
        exgcd(b, 13, x, y);
        x = (x % 13 + 13) % 13;
        printf("%d\n", (a * x) % 13);
    }
    return 0;
}

费马小定理

关于费马小定理的正确性这里就不证明了。

我们知道,假设p是一个质数 \(a ^ {p-1} \equiv 1 (mod \ p)\)
同样的我们就可以得到 \(a ^ {p-2} \equiv a ^ {-1} (mod \ p)\)
所以其核心我们就可以变成一个快速幂了。

代码

/*
    Code by lifehappy 2020:04:23
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
ll quick_pow(ll b, ll n) {
    ll ans = 1, po = b;
    while(n) {
        if(n & 1)   ans = (ans * po) % mod;
        po = (po * po) % mod;
        n >>= 1;
    }
    return ans;
}
int main() {
    ll a, b;
    while(cin >> a >> b) {//计算(a / b) % mod;
        b = quick_pow(b, mod - 2);
        cout << (a * b) % mod << endl;
    }
    return 0;
} 

线性求解逆元

我们先假定 \(p = k * i + j\ 1 < i < p, j < i\)

我们可以得到\(p = k * i + j \equiv 0(mod\ p)\)

对两边同时乘以\(i ^ {-1}, j ^ {-1}\)

得到\(k * j ^ {-1} + i ^ {-1} \equiv 0(mod\ p)\)

有\(i ^ {-1} \equiv -k * j {-1}\)

因为j < i 我们可以通过这个递推关系得到

\(a[i] = -(p / i) * a[p \% i]\)从而的到（1 ~ n)的逆元。

在此之前我们还得知道\(1 ^{-1} \equiv 1(mod\ p)\)

代码

/*
    Code by lifehappy 2020:04:23
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 1e3 + 10, mod = 1e9 + 7;
ll a[N];
int main() {
    a[1] = 1;
    for(ll i = 2; i < N; i++) {
        a[i] = -(mod / i) * a[mod % i];
        a[i] = (a[i] % mod + mod) % mod;
    }
    for(int i = 1; i <= 10; i++)
        printf("%lld  %lld\n", a[i], ((long long)i * a[i]) % mod);
    return 0;
}

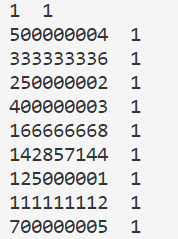
上面代码运行情况