Andrew 算法（构造凸包）
简要
这是一个基 \(Graham\) 思想的又一个算法，我个人认为其中复杂度的改进应该是在\(sort\) 的 \(cmp\) 部分吧，
\(Graham\) 的 \(cmp\) 部分需要对两个点算出叉乘，甚至在某些情况还要算出两个点的距离，这一步骤应该相对而言复杂度是较高的。
而 \(Andrew\) 很好的避免了这一步骤，直接通过对点的 \(x, y\) 的简单排序就可以实现一个 \(nlogn\) 的算法
算法思想
-
首先我们要对所有的点进行排序，通常情况下是按照，\(X\) 从小到大，如果 \(X\) 相等的话，按照 \(Y\) 从小到大。
这里有一点我们必须明白，排序后，最前面和最后面的点一定是极点。 -
接着就是进行 \(Graham\) 算法的重要的一步 \(Scan\)。
第一遍 \(Scan\) 我们从最左端的点出发，做一遍 \(Scan\) 我们可以得到整个凸包的下部分。
第二遍 \(Scan\) 我们从最右端的点出发，做一遍 \(Scan\) 我们可以得到整个凸包的上部分。
这两份 \(Scan\) 合并起来就是完整的凸包了。
实现图例
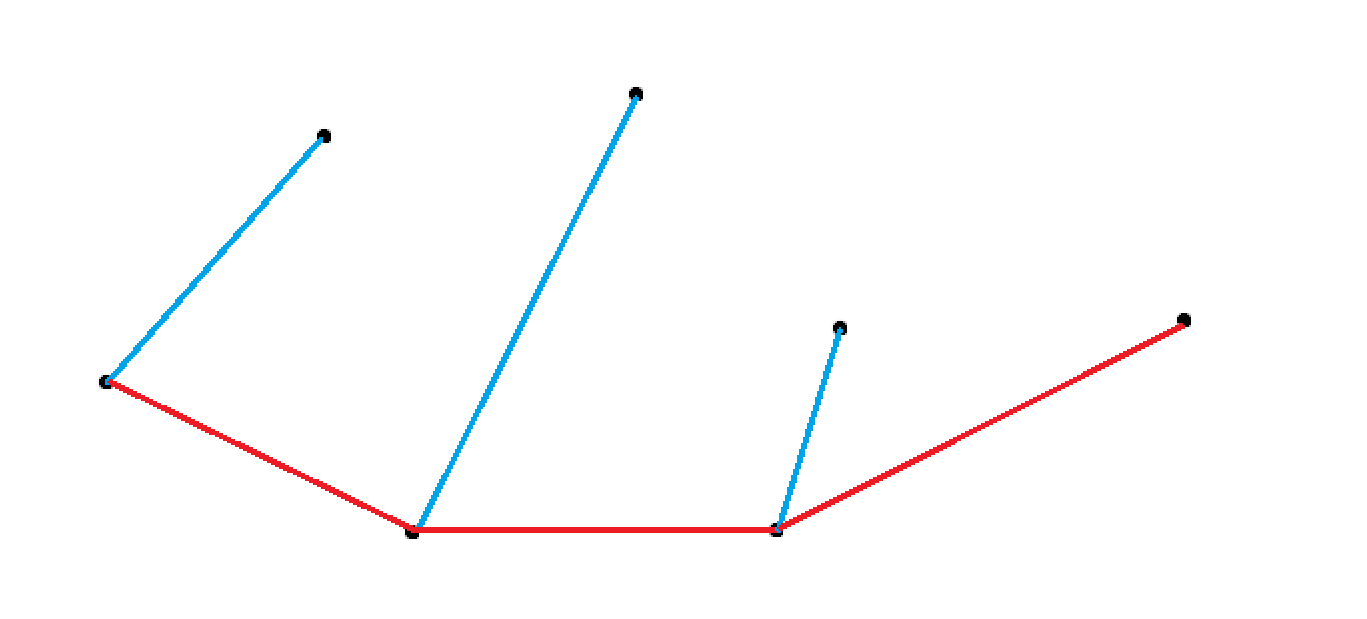
这是第一遍 \(Scan\)，蓝色的代表曾经走过，但是因为与后面的点构成凸包矛盾而进行过回溯。红色的线代表这一趟扫描满足条件的级边，也就是构成凸包的下半部分的边。
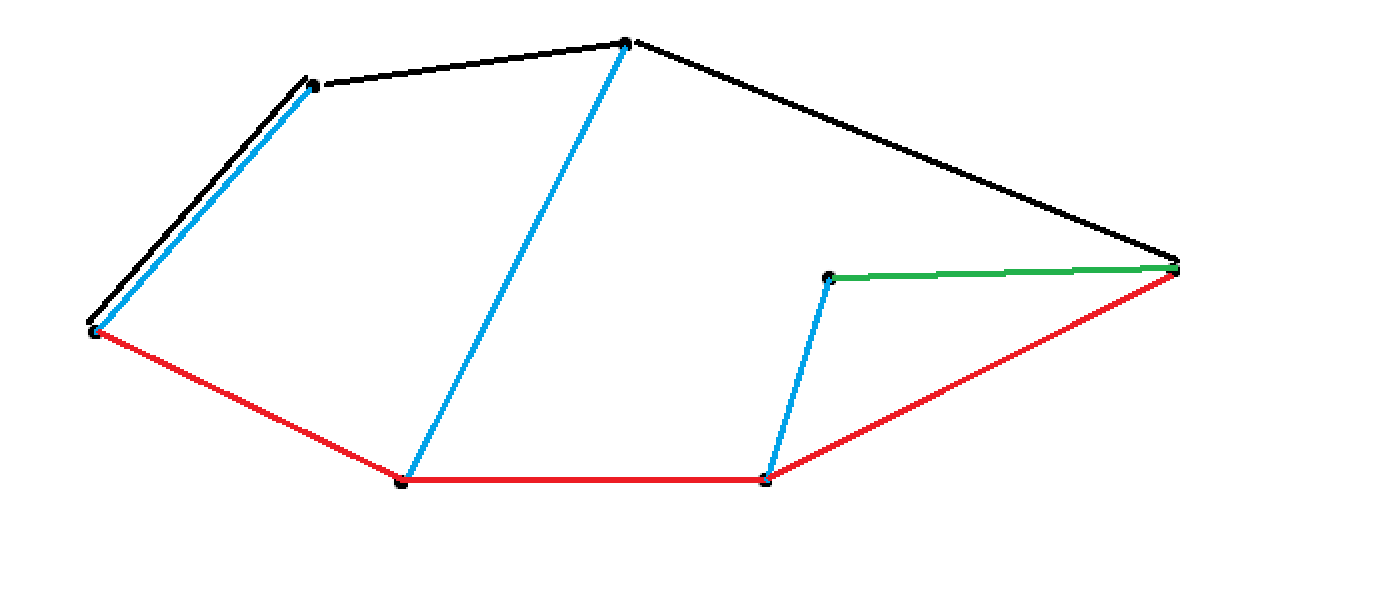
这是第二遍 \(Scan\)，绿色的代表曾经走过，但是因为与后面的点构成凸包矛盾而进行过回溯。黑色的线代表这一趟扫描满足条件的级边，也就是构成凸包的上半部分的边。
时间复杂度分析
\(sort\) 的时间是 \(O(nlogn)\) 两趟 \(scan\) 的时间都是线性的，整地复杂度是 \(O(nlogn)\)，但是我们认为这个算法的时间复杂度是优于 \(graham\) 的，原因应该是我在开头提到的把
模板题
P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包
学习过程中\(debug\)很乱的代码
/*
Code by lifehappy 2020:04:17
凸包Andrew算法
*/
#include<bits/stdc++.h>
using namespace std;
const double INF = 1e100;
const double eps = 1e-8;
const double pi = acos(-1.0);
const int N = 1e5 + 10;
int n, cnt, m;
int sgn(double x) {
if(fabs(x) < eps) return 0;
if(x > 0) return 1;
return -1;
}
struct point {
double x, y;
point(double a = 0.0, double b = 0.0) : x(a), y(b) {}
bool operator < (point t) {
if(sgn(x - t.x) == 0) return y < t.y;
return x < t.x;
}
}p[N], ans[N], all[N];
point operator - (point a, point b) {
return point(a.x - b.x, a.y - b.y);
}
double dis(point a, point b) {
a = a - b;
return sqrt(a.x * a.x + a.y * a.y);
}
double cross(point a, point b) {
return a.x * b.y - a.y * b.x;
}
void Andrew() {
sort(p, p + n);
int p1 = 0, p2;
for(int i = 0; i < n; i++) {
while(p1 > 1 && sgn(cross(ans[p1 - 1] - ans[p1 - 2], p[i] - ans[p1 - 2])) == -1) p1--;
ans[p1++] = p[i];
}
// cout << p1 << endl;
// for(int i = 0; i < p1; i++) {
// int flag = 1;
// for(int j = 0; j < m; j++)
// if(sgn(ans[i].x - all[j].x) == 0 && sgn(ans[i].y - all[j].y) == 0) {
// flag = 0;
// break;
// }
// printf("%lf %lf %s\n", ans[i].x, ans[i].y, flag ? "False" : " True");
// }
// cout << p1 << endl;
p2 = p1;
for(int i = n - 2; i>= 0; i--) {
while(p2 > p1 && sgn(cross(ans[p2 - 1] - ans[p2 - 2], p[i] - ans[p2 - 2])) == -1) p2--;
ans[p2++] = p[i];
// cout << p2 << endl;
}
// for(int i = 0; i < p2; i++)
// printf("%lf %lf\n", ans[i].x, ans[i].y);
// p2--;
p2--;
// for(int i = p1; i < p2; i++) {
// int flag = 1;
// for(int j = 0; j < m; j++)
// if(sgn(ans[i].x - all[j].x) == 0 && sgn(ans[i].y - all[j].y) == 0) {
// flag = 0;
// break;
// }
// printf("%lf %lf %s\n", ans[i].x, ans[i].y, flag ? "False" : " True");
// }
// cout << p2 << endl;
double target = 0.0;
for(int i = 0; i < p2; i++)
target += dis(ans[i], ans[i + 1]);
printf("%.2f\n", target);
}
int main() {
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// scanf("%d", &m);
// for(int i = 0; i < m; i++)
// scanf("%lf %lf", &all[i].x, &all[i].y);
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%lf %lf", &p[i].x, &p[i].y);
Andrew();
// point a(-9934.480000, -2886.200000), b(-9595.260000, -1905.480000), c(-9124.100000, -4804.250000);
// printf("%lf\n", cross(b - a, c - a));
return 0;
}
较为简洁的代码
/*
Code by lifehappy 2020:04:17
凸包Andrew算法
*/
#include<bits/stdc++.h>
using namespace std;
const double INF = 1e100;
const double eps = 1e-8;
const double pi = acos(-1.0);
const int N = 1e5 + 10;
int n, cnt, m;
int sgn(double x) {
if(fabs(x) < eps) return 0;
if(x > 0) return 1;
return -1;
}
struct point {
double x, y;
point(double a = 0.0, double b = 0.0) : x(a), y(b) {}
bool operator < (point t) {
if(sgn(x - t.x) == 0) return y < t.y;
return x < t.x;
}
}p[N], ans[N], all[N];
point operator - (point a, point b) {
return point(a.x - b.x, a.y - b.y);
}
double dis(point a, point b) {
a = a - b;
return sqrt(a.x * a.x + a.y * a.y);
}
double cross(point a, point b) {
return a.x * b.y - a.y * b.x;
}
void Andrew() {
sort(p, p + n);
int p1 = 0, p2;
for(int i = 0; i < n; i++) {
while(p1 > 1 && sgn(cross(ans[p1 - 1] - ans[p1 - 2], p[i] - ans[p1 - 2])) == -1) p1--;
ans[p1++] = p[i];
}
p2 = p1;
for(int i = n - 2; i>= 0; i--) {
while(p2 > p1 && sgn(cross(ans[p2 - 1] - ans[p2 - 2], p[i] - ans[p2 - 2])) == -1) p2--;
ans[p2++] = p[i];
}
p2--;
double target = 0.0;
for(int i = 0; i < p2; i++)
target += dis(ans[i], ans[i + 1]);
printf("%.2f\n", target);
}
int main() {
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%lf %lf", &p[i].x, &p[i].y);
Andrew();
return 0;
}
