C基础 寻找随机函数的G点
引言
随机函数算法应该是计算机史上最重要的十大算法之一吧. 而C中使用的随机函数
#include <stdlib.h> _Check_return_ _ACRTIMP int __cdecl rand(void);
本文主要围绕rand 函数找到G点. 就是伪随机函数的周期值.
关于rand 源码, 可以从Linux底层源码 glibc中找. 看了一下大约4个文件. 算法比较复杂. 感觉很稳定.
这里不探讨随机算法的实现. 只为了找到 随机函数周期.
前言
现在window上测试. 测试代码 main.c
#include <stdio.h> #include <stdlib.h> #define _INT_R (128) #define _INT_FZ (10000000) // 得到rand() 返回值, 并写入到文件中 int getrand(long long *pcut) { static int _cut = 0; long long t = *pcut + 1; int r = rand(); // 每次到万再提醒一下 if(t % _INT_FZ == 0) fprintf(stdout, "%d 个数据跑完了[%d, %lld]\n", _INT_FZ, _cut, t); if(t < 0) { // 数据超标了 ++_cut; fprintf(stderr, "Now %d T > %lld\n", _cut, t - 1); *pcut = 0; // 重新开始一轮 } *pcut = t; return r; } /* * 验证 rand 函数的周期 */ int main(int argc, char* argv[]) { int rbase[_INT_R]; int i = -1, r; long long cut = 0; // 先产生随机函数 while(++i < _INT_R) rbase[i] = getrand(&cut); // 这里开始随机了 for(;;) { r = getrand(&cut); if (r != rbase[0]) continue; for(i=1; i<_INT_R; ++i) { r = getrand(&cut); if(r != rbase[i]) break; } // 找见了数据 if(i == _INT_R) { printf("Now T = %lld\n", cut); break; } } system("pause"); return 0; }
主要思路是 _INT_R 128个数重叠那我们就认为. 已经找到这个周期了.
测试结果截图是
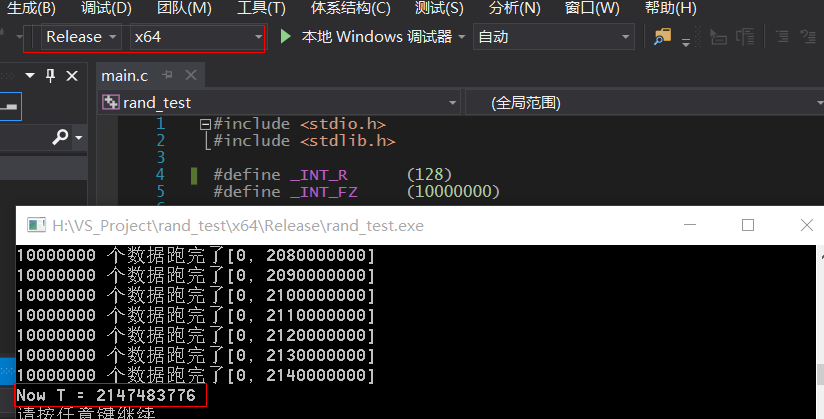
主要采用 Release X64 编译. 为了检验上面结果是可以接受的, 将 _INT_R 改成1024 重新编译一次.
运行结果如下:
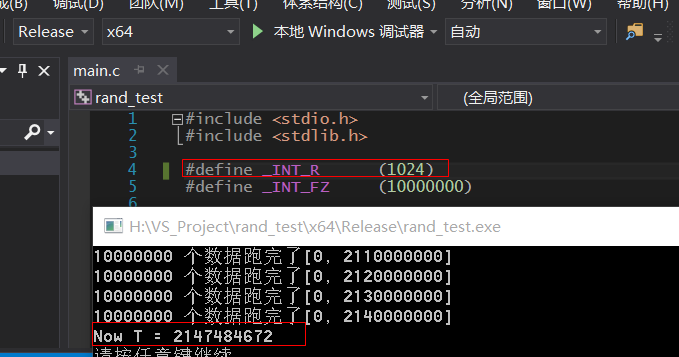
综合上面我们找见了 window 上 rand 函数的 G点 是
2147483776 - 128 = 214748248
2147484672 - 1024 = 2147483648
因而得到 window 上 VS2015 编译器的 rand G点 是 2147483648.
G点在游戏中用的很多. 例如抽奖, 掉装备, 暴击等等.
正文
1. 在linux 上试试水
在linux上试试 测试代码基本一样 rand2.c 如下
#include <stdio.h> #include <stdlib.h> #define _INT_R (1024) #define _INT_FZ (100000000) // 得到rand() 返回值, 并写入到文件中 int getrand(long long *pcut) { static int _cut = 0; long long t = *pcut + 1; int r = rand(); // 每次到万再提醒一下 if(t % _INT_FZ == 0) fprintf(stdout, "%d个数据又跑完了[%d, %lld]\n", _INT_FZ, _cut, t); if(t < 0) { // 数据超标了 ++_cut; fprintf(stderr, "Now %d T > %lld\n", _cut, t - 1); *pcut = 0; // 重新开始一轮 } *pcut = t; return r; } /* * 验证 rand 函数的周期 */ int main(int argc, char* argv[]) { int rbase[_INT_R]; int i = -1, r; long long cut = 0; // 先产生随机函数 while(++i < _INT_R) rbase[i] = getrand(&cut); // 这里开始随机了 for(;;) { r = getrand(&cut); if (r != rbase[0]) continue; for(i=1; i<_INT_R; ++i) { r = getrand(&cut); if(r != rbase[i]) break; } // 找见了数据 if(i == _INT_R) { printf("Now T = %lld\n", cut); break; } } return 0; }
编译命令
gcc -03 -o randc2.out rand2.c
最后运行结果, 等了 好久还是没出来.

Linux 上的rand 函数写的很有水准, 分布的很随机. 总而言之这个随机值比较大. 但一定存在的.
有兴趣的可以按照上面思路优化跑一跑. 这边Ubuntu 是虚拟机跑的慢.
2. 继续扩展, 减小rand 返回 MAX值 试试水
修改上面 getrand 函数
// _INT_RMAX 表示随机数范围 [0, 100) #define _INT_RMAX (100) #define _INT_R (1024) #define _INT_FZ (10000000) // 得到rand() 返回值, 并写入到文件中 int getrand(long long *pcut) { static int _cut = 0; long long t = *pcut + 1; int r = rand() % _INT_RMAX; // 每次到万再提醒一下 if (t % _INT_FZ == 0) fprintf(stdout, "%d 个数据跑完了[%d, %lld]\n", _INT_FZ, _cut, t); if (t < 0) { // 数据超标了 ++_cut; fprintf(stderr, "Now %d T > %lld\n", _cut, t - 1); *pcut = 0; // 重新开始一轮 } *pcut = t; return r; }
添加 了 取余看是否, 影响G点 测试结果
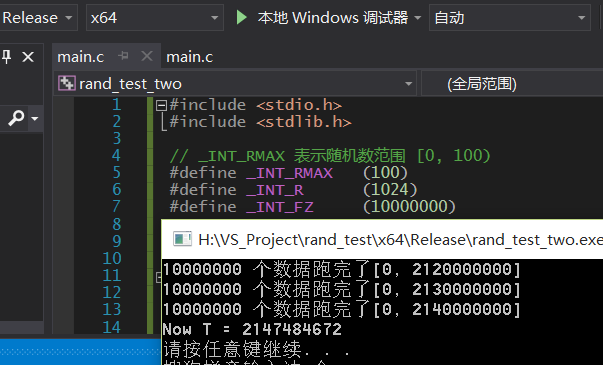
发现G点没有变化.
可以有推论: rand() 周期不随着 二次 mod取余而改变.
因而可以放心 mod使用 伪随机函数. G点还是那么大.
3. 最后, 赠送一个常用的 [min, max] 之间的随机函数
/* * 返回 [min, max] 区间的随机函数 * min : 起始位置 * max : 结束位置 * : 返回[min, max]区间之内的位置 */ extern int random(int min, int max); /* * 返回 [min, max] 区间的随机函数 * min : 起始位置 * max : 结束位置 * : 返回[min, max]区间之内的位置 */ int random(int min, int max) { assert(min < max); // 正常情况 return rand() % (max - min + 1) + min; }
测试demo 代码 结构如下
#include <stdio.h> #include <stdlib.h> #include <time.h> #include <assert.h> /* * 返回 [min, max] 区间的随机函数 * min : 起始位置 * max : 结束位置 * : 返回[min, max]区间之内的位置 */ extern int random(int min, int max); /* * C 基础, 使用随机函数 */ int main(int argc, char* argv[]) { int min = -5, max = 5; int i = 0; // 开始统一 初始化种子 srand((unsigned)time(NULL)); while(i < 100) { printf("%3d ", random(min, max)); if (++i % 10 == 0) putchar('\n'); } system("pause"); return 0; } /* * 返回 [min, max] 区间的随机函数 * min : 起始位置 * max : 结束位置 * : 返回[min, max]区间之内的位置 */ int random(int min, int max) { assert(min < max); // 正常情况 return rand() % (max - min + 1) + min; }
测试结果是

基本比较稳定. 一切都在预料之中.
总结 本文 得出两个 推论
a. rand()伪随机函数, 存在G点. 并且可以找到
b. G点 不随着 二次 mod 取余改变.
后记
错误是难免的, 预祝明天愉快~~




