浮点数精度上误差
在我刚接触编程的时候, 那时候面试小题目很喜欢问下面这几类问题
1' 浮点数如何和零比较大小?
2' 浮点数如何转为整型?
然后过了七八年后这类问题应该很少出现在面试中了吧. 刚好最近我遇到线上 bug, 同大家交流科普下
问题最小现场
#include <stdio.h> int main(void) { float a = 2.01f; double b = 2.01; printf("a1 : 2.01 * 1000 = %f\n", a * 1000); // a1 : 2.01 * 1000 = 2010.000000 printf("a2 : int(2.01 * 1000) = %d\n", (int)(a * 1000)); // a2 : int(2.01 * 1000) = 2010 printf("b1 : 2.01 * 1000 = %lf\n", b * 1000); // b1 : 2.01 * 1000 = 2010.000000 printf("b2 : int(2.01 * 1000) = %d\n", (int)(b * 1000)); // b2 : int(2.01 * 1000) = 2009 }
(用 Go Java 效果是一样的, 绝大部分实现都是严格遵循 IEEE754 标准
问题解答
其中 a1 和 b1 在 C 中 等价于下面的代码
float a = 2.01f; double b = 2.01; printf("a1 : 2.01 * 1000 = %f\n", (double)(a * 1000)); printf("b1 : 2.01 * 1000 = %f\n", b * 1000);
其中 printf float 其实相当于 printf (double) 去处理的. 具体可以看这类源码
#define PARSE_FLOAT_VA_ARG(INFO) \ do \ { \ INFO.is_binary128 = 0; \ if (is_long_double) \ the_arg.pa_long_double = va_arg (ap, long double); \ else \ the_arg.pa_double = va_arg (ap, double); \ } \ while (0)
其次二者输出打印的数据内容一样. 本质原因是, double 尾数的高23位和float的尾数23位一样.
如果你用 %.8f 可能就不一样了.
(float : 1 + 8 +23, 小数点后精度 6-7)
(double : 1 + 11 + 52, 小数点后精度 15-16)
简单的, 我们可以用下面代码去验证
#include <stdio.h> static void print_byte(unsigned char byte) { printf("%d%d%d%d%d%d%d%d" , ((byte >> 7) & 1) , ((byte >> 6) & 1) , ((byte >> 5) & 1) , ((byte >> 4) & 1) , ((byte >> 3) & 1) , ((byte >> 2) & 1) , ((byte >> 1) & 1) , ((byte >> 0) & 1) ); } static void print_number(const void * data, size_t n) { const unsigned char * bytes = data; # if __BYTE_ORDER__ == __ORDER_LITTLE_ENDIAN__ for (size_t i = n; i > 0; i--) { print_byte(bytes[i-1]); } # else for (size_t i = 0; i < n; i++) { print_byte(bytes[i]); } # endif } static void print_float(float num) { printf(" float = "); print_number(&num, sizeof num); printf("\n"); } static void print_double(double num) { printf("double = "); print_number(&num, sizeof num); printf("\n"); } int main(void) { float a = 2.01f; double b = 2.01; print_float(a); print_double(b); printf(" float 2.01f + %%.%df = %.*f\n", 8, 8, a); printf("double 2.01 + %%.%df = %.*lf\n", 8, 8, b); }
在 window 和 ubuntu 得到的测试数据如下
/* float = 01000000000000001010001111010111 double = 0100000000000000000101000111101011100001010001111010111000010100 float 2.01f = 0 10000000 00000001010001111010111 double 2.01 = 0 10000000000 00000001010001111010111 00001010001111010111000010100 float 2.01f + %.6f = 2.010000 double 2.01 + %.6f = 2.010000 float 2.01f + %.7f = 2.0100000 double 2.01 + %.7f = 2.0100000 float 2.01f + %.8f = 2.00999999 double 2.01 + %.8f = 2.01000000 float 2.01f + %.10f = 2.0099999905 double 2.01 + %.10f = 2.0100000000 float 2.01f + %.15f = 2.009999990463257 double 2.01 + %.15f = 2.010000000000000 float 2.01f + %.16f = 2.0099999904632568 double 2.01 + %.16f = 2.0099999999999998 float 2.01f + %.17f = 2.00999999046325684 double 2.01 + %.17f = 2.00999999999999979 */
明显可以看出来 a = 2.01f 和 b = 2.01 在内存中二者是不一样的. 即 a != b, a * 1000 != b * 1000. 有兴趣的可以自行去实验.
问题解答继续
这里说说 a2 和 b2 case 造成的原因.
printf("a2 : int(2.01 * 1000) = %d\n", (int)(a * 1000)); // a2 : int(2.01 * 1000) = 2010 printf("b2 : int(2.01 * 1000) = %d\n", (int)(b * 1000)); // b2 : int(2.01 * 1000) = 2009
我们首先获取其内存布局
float 2010.0f = 0 10001001 11110110100000000000000 double 2010.0 = 0 10000001001 1111011001111111111111111111111111111111111111111111
随后借助场外信息, 引述 <<深入理解计算机系统-第三版>> 部分舍入概念
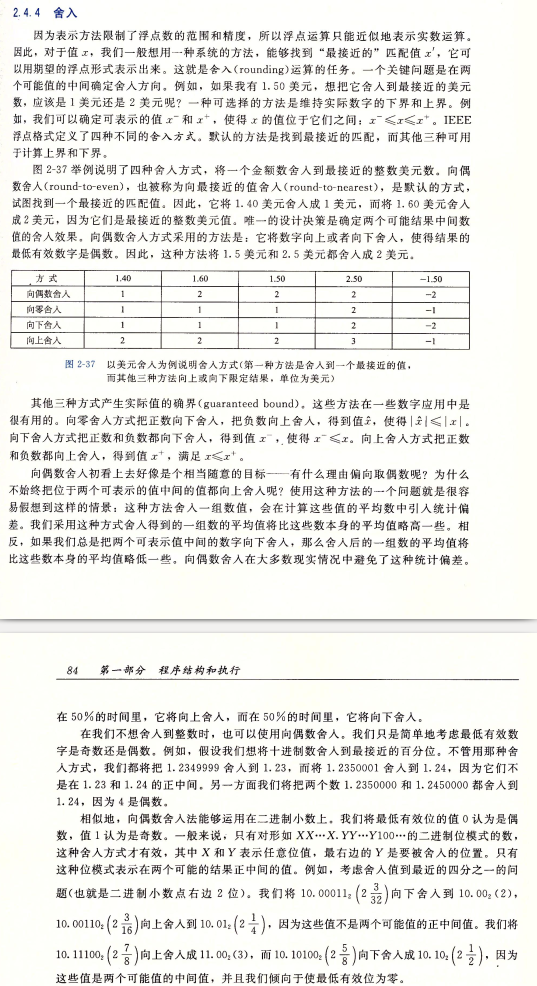
误差来自浮点数无法精确表示和转换过程中舍入起的效果.
问题反思
这类问题, 或多或少遇到过, 希望我们这里对这类问题做个了结 ~
此刻不知道有心人会不会着急下结论,
那以后的业务中还是别用 float 了, 或者直接用 double, 或者定点小数, 或者整数替代 float 等等 ...
这么考虑很不错, 在大多数领域是完全没有问题的. 也是值得推荐的.
补充下, 也有些领域例如嵌入式, 他们还是会用 float, 因为对他们而言 double 有的时候太浪费内存了,
还存在着地址对齐等问题.
虽然不同领域(场景)会有不同方式方法, 但有一点需要大家一块遵守, 没有特殊情况别混着用 ~
希望以上能帮助朋友们对这类问题知其所以然 ~
后记 - 再见, 祝好运 ~
错误是难免的, 欢迎交流指正, 当找个乐子 ~ 哈哈哈 ~


