DCP-DEC:Deep Embedded Clustering with Distribution Consistency Preservation for Attributed Networks
论文阅读11-DCP-DEC:Deep Embedded Clustering with Distribution Consistency Preservation for Attributed Networks
论文信息
代码地址：Zhengymm/DCP (github.com)
1.存在问题
- 存在问题
在不同视图数据一致性的假设下，网络拓扑的拓扑结构和节点属性的簇结构对于属性网络应该是一致的。然而，许多现有方法忽略了这个属性，即使它们分别对网络拓扑和节点属性的节点表示进行编码，同时将节点聚类在从其中一个视图学习的表示向量上。：缺少一致性
由于图卷积网络（GCN）提供了一种将链接结构和节点特征平滑结合的方法，最近的一些 DEC 模型采用 GCN 作为主干，以弥补以前忽略拓扑信息的方法的不足，并获得更好的聚类性能对于属性网络 。
- DAEGC利用图注意力网络 (GAT) 形成自动编码器深度聚类框架，但缺乏节点属性的重建，而节点属性是自监督学习中的一项有用技术
- SDCN 融合自动编码器和 GCN，以自我监督的方式学习节点表示和隐藏的集群分布。但是，它忽略了重建网络拓扑。我们认为重建原始网络（包括拓扑和节点属性）将有利于学习节点表示。同时，值得研究的是如何将网络学习到的隐藏向量投影到集群分布中并保持实际的集群结构。
- 多视图聚类的一致性，网络拓扑的聚类结构和节点属性的聚类结构对于属性网络应该是一致的。我们建议在 DEC 过程中从不同视图获得的聚类分布的一致性约束比（或可以替代）在聚类之前融合两个表示向量更稳健。
2. 研究属性图聚类方法
1. 研究属性聚类方法
现有的属性网络聚类深度模型大致可以分为两类。第一种利用网络嵌入的方法利用深度学习技术获得低维表示向量，然后采用典型的聚类方法，如K-means或谱聚类，来获取节点集群。我们称这种方法为“双阶段方法”。
“双阶段方法高度依赖于深度模型的表示学习能力，学习到的表示可能不适合节点聚类的任务，尽管它们也可以直接用于节点分类和链路预测等其他下游任务.
第二类深度嵌入式聚类 (DEC) 方法直接将聚类和表示学习的目标集成到一个统一的框架中。我们称这种方法为“单阶段方法”。
通过联合优化，DEC模型能够同时学习节点表示和相应的簇结构，从而获得收益并相互促进。现有研究表明，用于节点聚类的单阶段端到端方法优于两阶段方法
论文解读（DEC）《Unsupervised Deep Embedding for Clustering Analysis》 - VX账号X466550 - 博客园 (cnblogs.com)
(57条消息) DEC(Deep Embedded Cluster)小结_dec聚类_AndyViky的博客-CSDN博客
DEC算法由两部分组成，第一部分会预训练一个AE模型；第二部分选取AE模型中的Encoder部分，加入聚类层，使用KL散度进行训练聚类。
3. 解决问题
- 如何解决
创新点：利用图形自动编码器和节点属性自动编码器分别学习节点表示和集群分配。此外，引入了分布一致性约束来保持两个视图的聚类分布的潜在一致性。
- 我们提出了一种用于属性网络的端到端深度嵌入式聚类模型，它利用GAE 和AE 从网络拓扑和节点属性中同时学习节点表示和聚类分配。
- 我们进一步引入分布一致性约束来保持两个集群分配的潜在一致性。
4.DCP-DEC model
1. model structrue
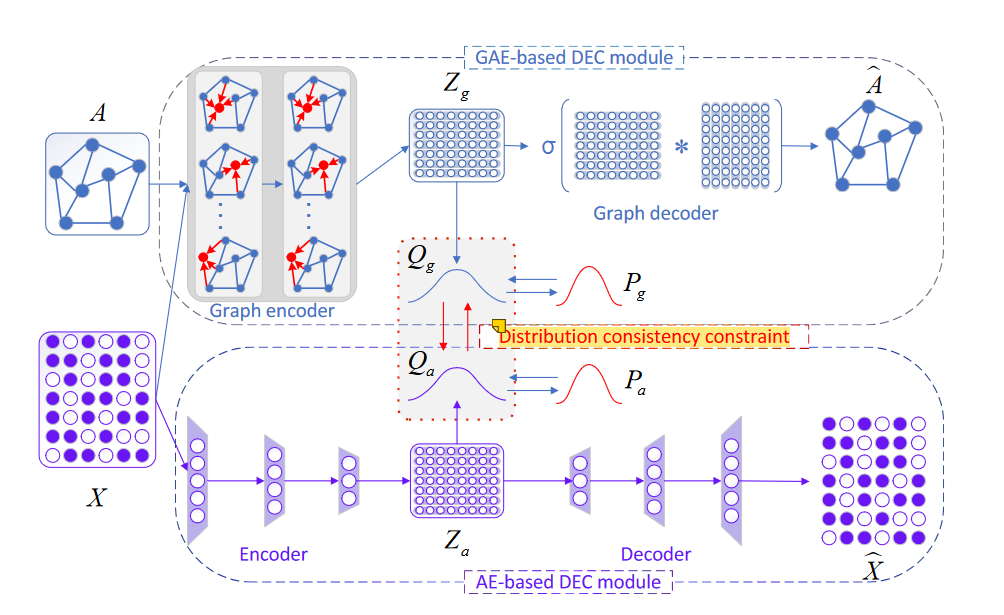
DCP-DEC模型主要由3个模块组成：基于 AE 的 DEC 模块、基于 GAE 的 DEC 模块、分布一致性约束。
- 基于 AE 的 DEC 模块：。该模块采用 DNN 对节点属性进行编码和解码，以学习节点的表示。利用得到的向量，我们通过Student's t分布得到每个节点的软聚类分配，然后相应地构造目标分布。在训练过程中，我们以统一的方式最小化解码器的重建损失和聚类损失，其中聚类损失的特征是目标分布与目标分布之间的 KL 散度。**
- 基于 GAE 的 DEC 模块：我们将网络结构和节点属性融合在一起，使用 GCN 编码器学习潜在表示，然后通过内积解码器重建链接连接以指导学习过程。网络拓扑结构通常非常稀疏，因此节点属性对于指导网络结构的重构非常有帮助。我们以网络拓扑结构作为主要信息来源，属性信息作为补充。
- 分布一致性约束：我们得到了两个使用不同信息和不同学习过程的聚类分配。基于不同视图数据一致性的假设，我们引入分布一致性约束来保持节点属性的簇结构和网络拓扑结构的一致性（由节点属性增强）。通过最小化上述两个模块的两个聚类分布之间的 KL 散度，我们可以获得更稳健和平滑的聚类结构，从而更好地融合两个不同的视图来完成属性网络聚类任务。
2.基于 AE 的 DEC 模块
编码器-解码器模块用于通过最小化原始数据和重建数据之间的重建损失来提取潜在表示。
基于 AE 的模块仅对节点属性进行编码以学习节点表示，并使用解码器重建输入。在本研究中，我们简单地使用全连接的 DNN 作为编码器来将每个节点的属性映射到非线性低维潜在表示向量。
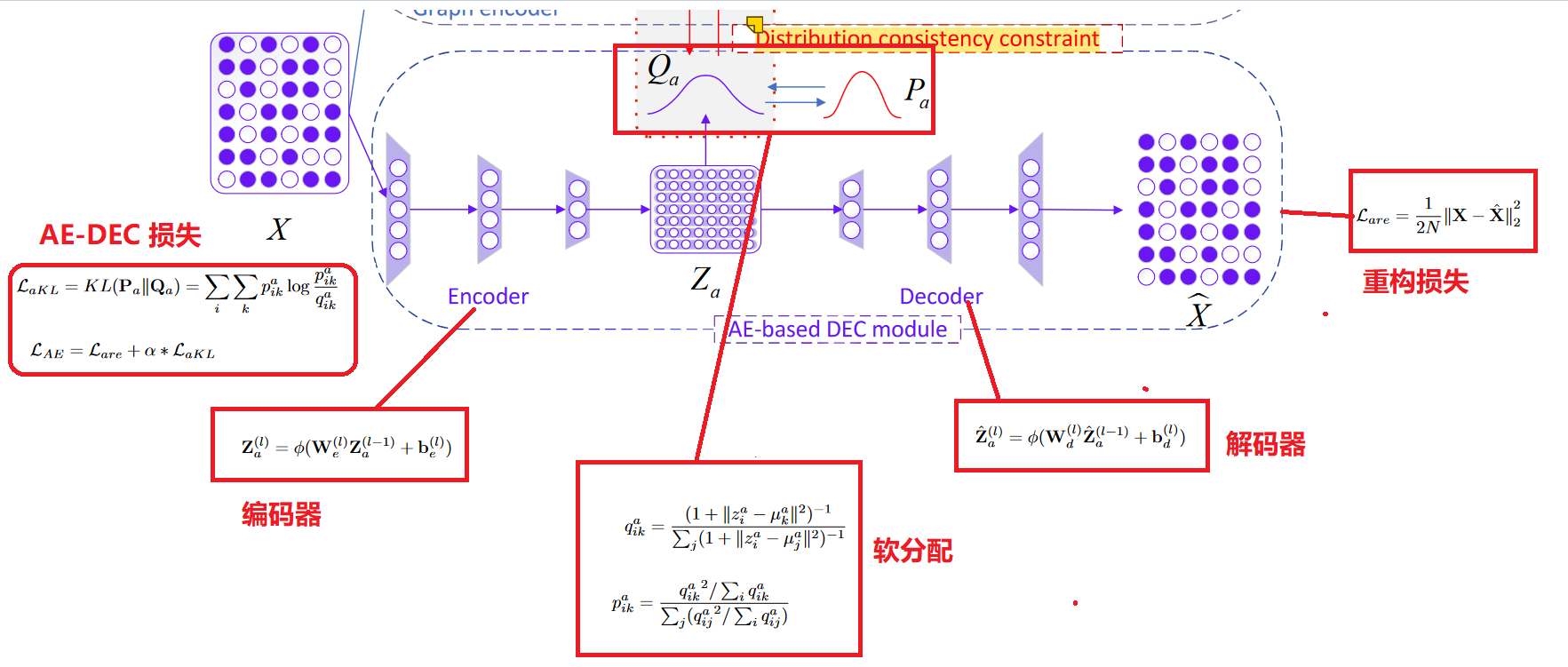
3.基于 GAE 的 DEC 模块
我们使用双层 GCN 作为编码器来学习节点表示，因为它具有在属性网络中保留信息的强大能力。
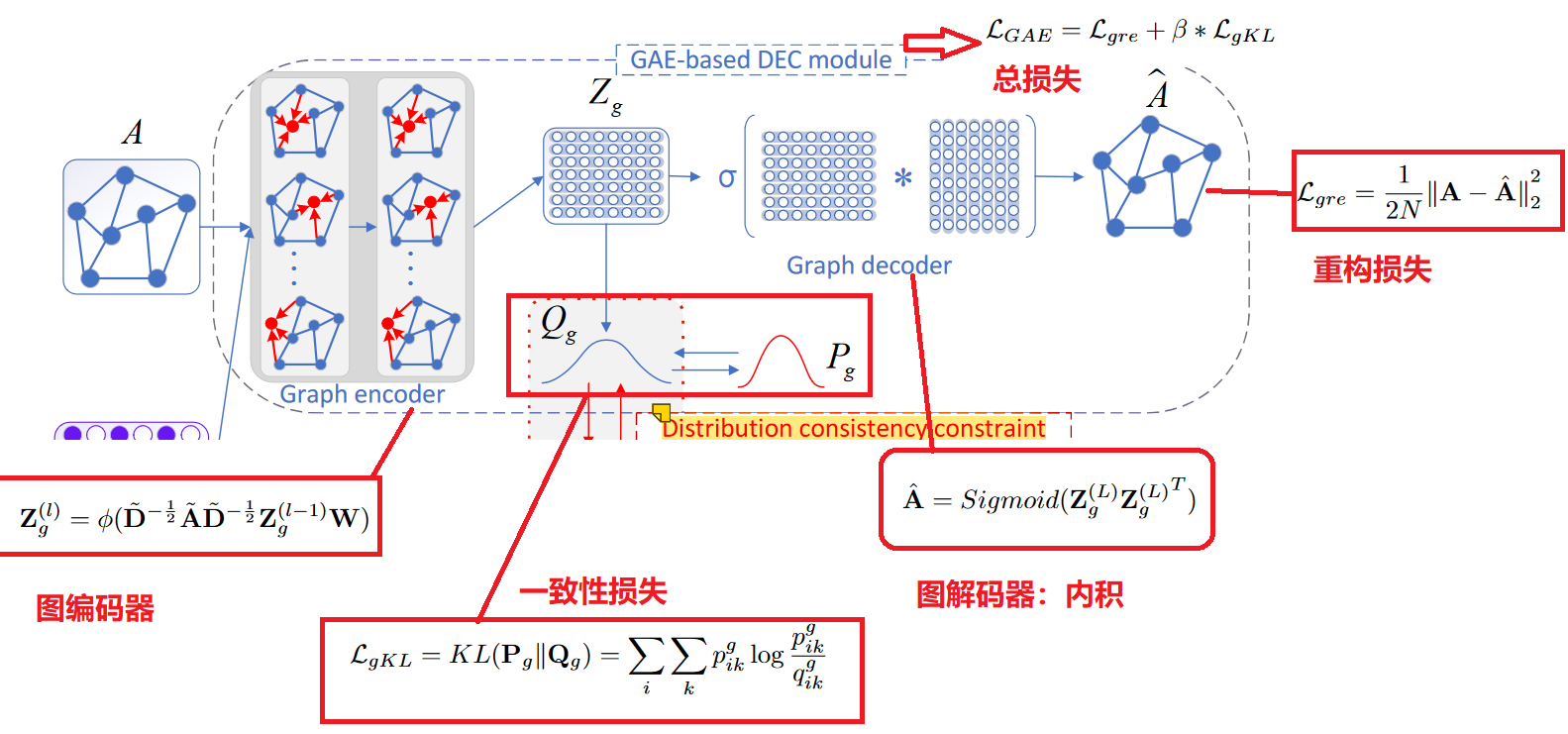
4. 分布一致性约束
我们可以从两个不同的深度嵌入式聚类模块（基于 AE 的 DEC 模块和基于 GAE 的 DEC 模块）中获得两个节点表示和聚类分布。在不同视图下数据对象的聚类一致性假设下，网络拓扑的聚类结构和节点属性的聚类结构对于属性网络应该是一致的。因此，我们提出聚类分布一致性约束，使从上述两个 DEC 模块中学习到的聚类分配尽可能一致。我们相信这种约束对于获得良好的聚类更为稳健，或者可以替代在聚类之前融合两个表示向量。
由于Qg是从同时利用拓扑和节点属性的GAE模块获得的，我们认为Qg(目标分布）比只考虑属性的Qa包含更丰富的信息。
DCP-DEC总损失：
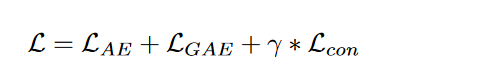
5.DCP-DEC算法流程图
6.DCP-DEC 代码
from __future__ import print_function, division
import argparse
import torch
import torch.nn as nn
import torch.nn.functional as F
from sklearn.cluster import KMeans
from torch.nn.parameter import Parameter
from torch.optim import Adam
from evaluation import eva
from utils import load_graph
from models import AE, GAE
import numpy as np
class DCP_DEC(nn.Module):
def __init__(self, n_enc_1, n_dec_1, n_input, n_z,
n_clusters, v=1):
super(DCP_DEC, self).__init__()
# autoencoder for intra information
self.ae = AE(n_enc_1=n_enc_1, n_dec_1=n_dec_1, n_input=n_input, n_z=n_z)
self.ae.load_state_dict(torch.load(args.dnn_pretrain_path, map_location='cpu'))
# cluster layer
self.dnn_cluster_layer = Parameter(torch.Tensor(n_clusters, n_z))
torch.nn.init.xavier_normal_(self.dnn_cluster_layer.data)
# GCN for inter information
self.gae = GAE(input_feat_dim=n_input, hidden_dim1=512, n_z=n_z)
self.gae.load_state_dict(torch.load(args.gcn_pretrain_path, map_location='cpu'))
# cluster layer
self.gcn_cluster_layer = Parameter(torch.Tensor(n_clusters, n_z))
torch.nn.init.xavier_normal_(self.gcn_cluster_layer.data)
# degree
self.v = v
def forward(self, x, adj):
# DNN Module
x_bar, dz = self.ae(x)
# GCN Module
a_bar, gz = self.gae(x, adj)
# Dual Self-supervised Module for DNN
q_dnn = 1.0 / (1.0 + (torch.sum(torch.pow(dz.unsqueeze(1) - self.dnn_cluster_layer, 2), 2) / self.v))
q_dnn = q_dnn.pow((self.v + 1.0) / 2.0)
q_dnn = (q_dnn.t() / torch.sum(q_dnn, 1)).t()
# Dual Self-supervised Module for GAE
q_gcn = 1.0 / (1.0 + (torch.sum(torch.pow(gz.unsqueeze(1) - self.gcn_cluster_layer, 2), 2) / self.v))
q_gcn = q_gcn.pow((self.v + 1.0) / 2.0)
q_gcn = (q_gcn.t() / torch.sum(q_gcn, 1)).t()
return x_bar, q_dnn, a_bar, q_gcn, dz, gz
def target_distribution(q):
weight = q ** 2 / q.sum(0)
return (weight.t() / weight.sum(1)).t()
def train_dcp(model, adj, data, y):
optimizer = Adam(model.parameters(), lr=args.lr)
# k-menas initial for cluster centers of AE-based module
with torch.no_grad():
_, dz = model.ae(data)
dnn_kmeans = KMeans(n_clusters=y.max()+1, n_init=20)
# print(dnn_kmeans)
y_dnnpred = dnn_kmeans.fit_predict(dz.data.cpu().numpy())
model.dnn_cluster_layer.data = torch.tensor(dnn_kmeans.cluster_centers_).to(device)
eva(y, y_dnnpred, 'dnn-pre')
# k-menas initial for cluster centers of GAE-based module
with torch.no_grad():
_, gz = model.gae(data, adj)
gcn_kmeans = KMeans(n_clusters=y.max()+1, n_init=20)
# print(gcn_kmeans)
y_gcnpred = gcn_kmeans.fit_predict(gz.data.cpu().numpy())
model.gcn_cluster_layer.data = torch.tensor(gcn_kmeans.cluster_centers_).to(device)
eva(y, y_gcnpred, 'gae-pre')
for epoch in range(args.epochs):
# adjust_learning_rate(optimizer, epoch)
if epoch % 1 == 0:
# update_interval
_, tmp_qdnn, _, tmp_qgcn, tmp_dz, tmp_gz = model(data, adj)
p_dnn = target_distribution(tmp_qdnn.data)
p_gcn = target_distribution(tmp_qgcn.data)
res1 = tmp_qdnn.data.cpu().numpy().argmax(1) # Q_dnn
res2 = p_dnn.data.cpu().numpy().argmax(1) # P_dnn
res3 = tmp_qgcn.data.cpu().numpy().argmax(1) # Q_gcn
res4 = p_gcn.data.cpu().numpy().argmax(1) # P_gcn
qdnn = eva(y, res1, str(epoch) + ' Q_DNN')
eva(y, res2, str(epoch) + ' P_DNN')
qgcn = eva(y, res3, str(epoch) + ' Q_GCN')
eva(y, res4, str(epoch) + ' P_GCN')
x_bar, q_dnn, a_bar, q_gcn, dz, gz = model(data, adj)
dnn_cluloss = F.kl_div(q_dnn.log(), p_dnn, reduction='batchmean') # dnn_cluster
dnn_reloss = F.mse_loss(x_bar, data) # dnn_reconstruction
gcn_cluloss = F.kl_div(q_gcn.log(), p_gcn, reduction='batchmean') # gcn_cluster
gcn_reloss = F.mse_loss(a_bar, adj.to_dense()) # gcn_reconstruction
# clustering distribution consistency
con_loss = F.kl_div(q_dnn.log(), q_gcn, reduction='batchmean') # GCN guide
ae_loss = args.alpha * dnn_cluloss + args.rae * dnn_reloss
gae_loss = args.beta * gcn_cluloss + 1.0 * gcn_reloss
loss = ae_loss + gae_loss + args.gamma * con_loss
optimizer.zero_grad()
loss.backward()
optimizer.step()
return qgcn, qdnn
if __name__ == "__main__":
parser = argparse.ArgumentParser(description='train',
formatter_class=argparse.ArgumentDefaultsHelpFormatter)
parser.add_argument('--name', type=str, default='acm')
parser.add_argument('--gpu', type=int, default=1)
parser.add_argument('--k', type=int, default=None)
parser.add_argument('--lr', type=float, default=1e-3)
parser.add_argument('--epochs', type=int, default=500)
parser.add_argument('--n_z', default=64, type=int)
parser.add_argument('--pretrain_path', type=str, default='pkl')
parser.add_argument('--alpha', type=float, default=1)
parser.add_argument('--beta', type=float, default=1)
parser.add_argument('--gamma', type=float, default=1)
parser.add_argument('--rae', type=int, default=1)
args = parser.parse_args()
print(args)
torch.cuda.set_device(args.gpu)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print("use cuda: {}".format(device))
args.dnn_pretrain_path = './pretrain/{}_ae.pkl'.format(args.name)
args.gcn_pretrain_path = './pretrain/{}_gae.pkl'.format(args.name)
np.random.seed(0)
torch.manual_seed(0)
# A / KNN Graph, feature and label
adj, feature, label = load_graph(args.name, args.k)
adj = adj.to(device)
feature = torch.FloatTensor(feature).to(device)
n_input = feature.shape[1]
n_clusters = label.max() + 1
model = DCP_DEC(512, 512, n_input=n_input, n_z=args.n_z, n_clusters=n_clusters, v=1).to(device)
print("Start training...............")
result_qgcn, result_qdnn = train_dcp(model, adj, feature, label)
print(".........................")
print("The result of Q-GAE:")
print(result_qgcn)
print("The result of Q-AE:")
print(result_qdnn)
print(".........................")
5. result Analysis
1. 数据集
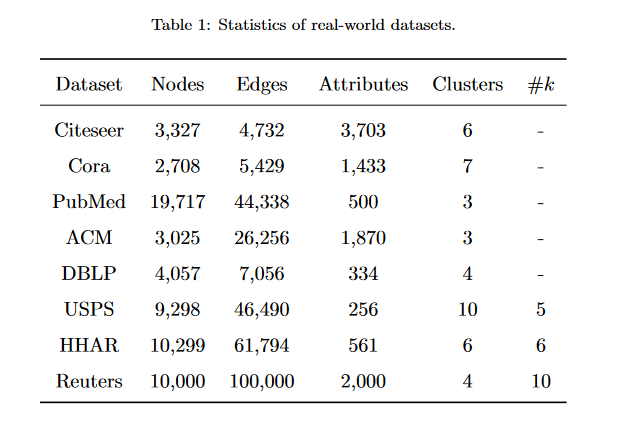
2. 实验结果
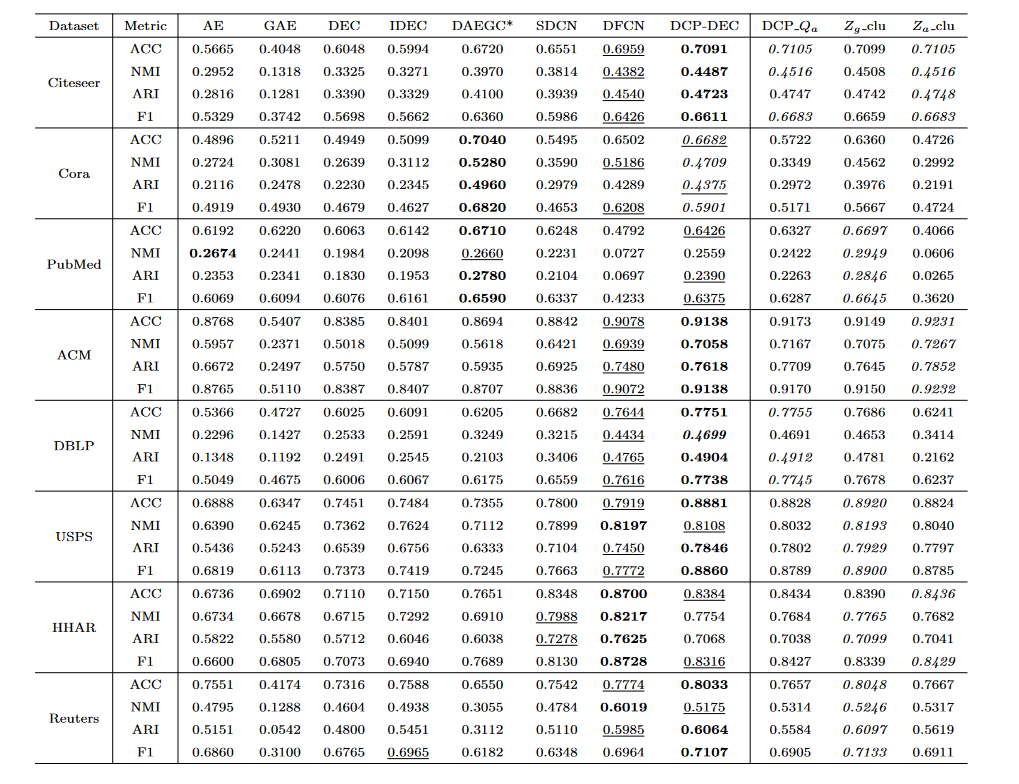
3.实验结果分析
- 单阶段DEC 模型始终优于比较的网络嵌入聚类方法。尽管 DFCN 看起来像是一种两阶段方法，但它在表示学习过程中采用三元组自监督策略作为节点聚类的指导，其使用与单阶段端到端模型相同的思想。这验证了在显式聚类约束下，学习到的表示向量可以产生更好的聚类结果。
- 对于深度嵌入式聚类模型，DEC 和 IDEC 仅利用节点特征，因此它们的性能比融合拓扑和属性信息的其他方法差。这也证明了综合考虑属性网络中两种信息的有效性。
- 我们的模型显示出对 SDCN 的显着改进。这有力地验证了我们的两个直觉。 1）重构网络拓扑有帮助。 2）集群分布约束是学习节点表示及其集群结构的良好指导。尽管我们的 DCP-DEC 模型在 Cora 和 PubMed 网络上不如 DAEGC ，在 HHAR 上不如 DFCN ，但性能仍然具有竞争力。此外，与 DFCN 相比，DCP-DEC 模型更简单.
- 对于 DCP-DEC 模型的四个变体，如果我们直接使用聚类分配作为最终聚类，结果是令人满意的。在大多数情况下，Qg和Qa的聚类分布趋于一致，证明了分布一致性约束的有效性。同时，Qg的结果强于Qa，说明选择Qg作为指导目标是合理的。
4. 消融实验:ablation
模块有效性验证
DCP-W/G 和 DCP-W/A 分别代表聚类结果基于GAE的模块和基于AE的模块没有一致性约束
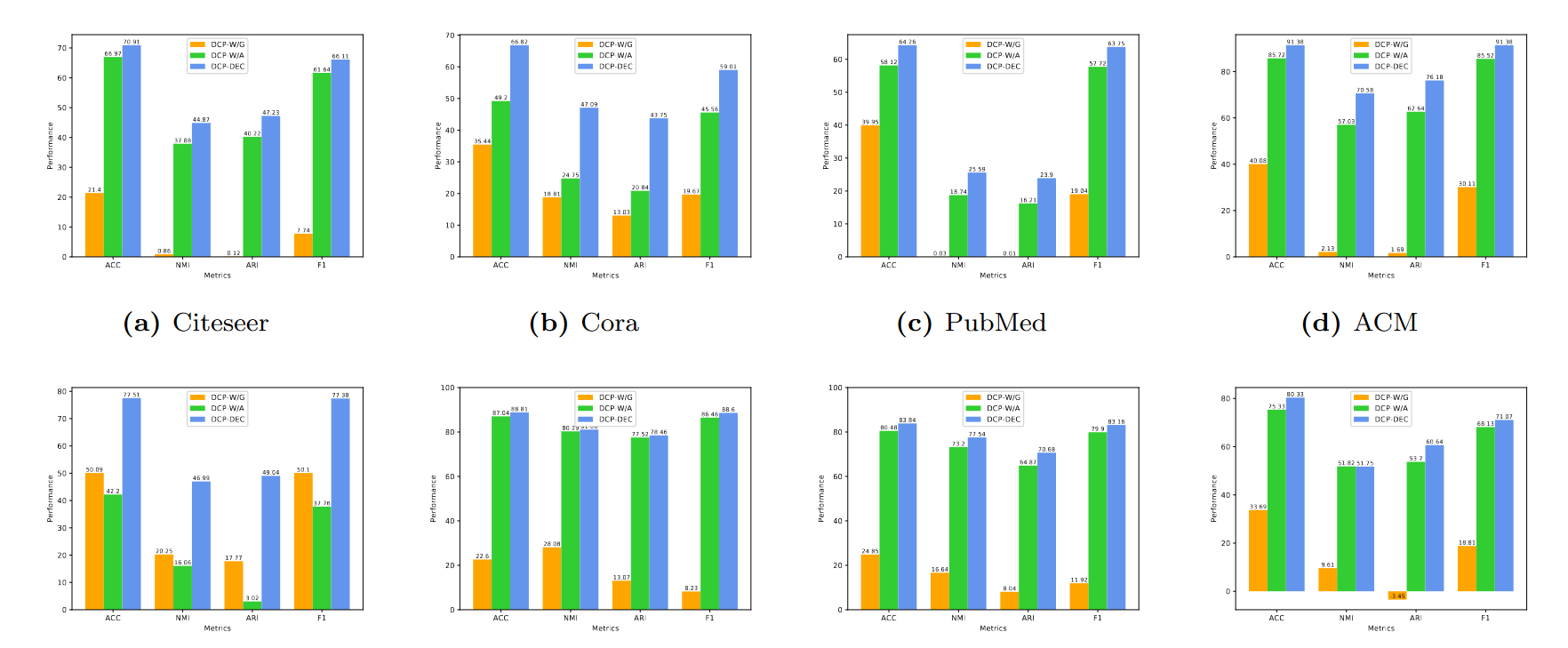
- DCP-DEC模型的结果显着实验结果比DCP-W/G和DCP-W/A要好。这表明了DCP-DEC中使用的分布一致性约束的有效性。
- 除DBLP网络外，DCP-W/A的结果通常优于DCP-W/G，验证了深度自动编码器对节点属性的重要性。
- DCP-DEC的整体性能表明，我们的框架利用了网络拓扑结构和节点属性，并提供了一种有效的方法来结合从两个视图中获得的两个集群分配。总而言之，分布一致性约束在我们的整个模型中发挥了重要作用。
隐藏层的数量和维度USPS
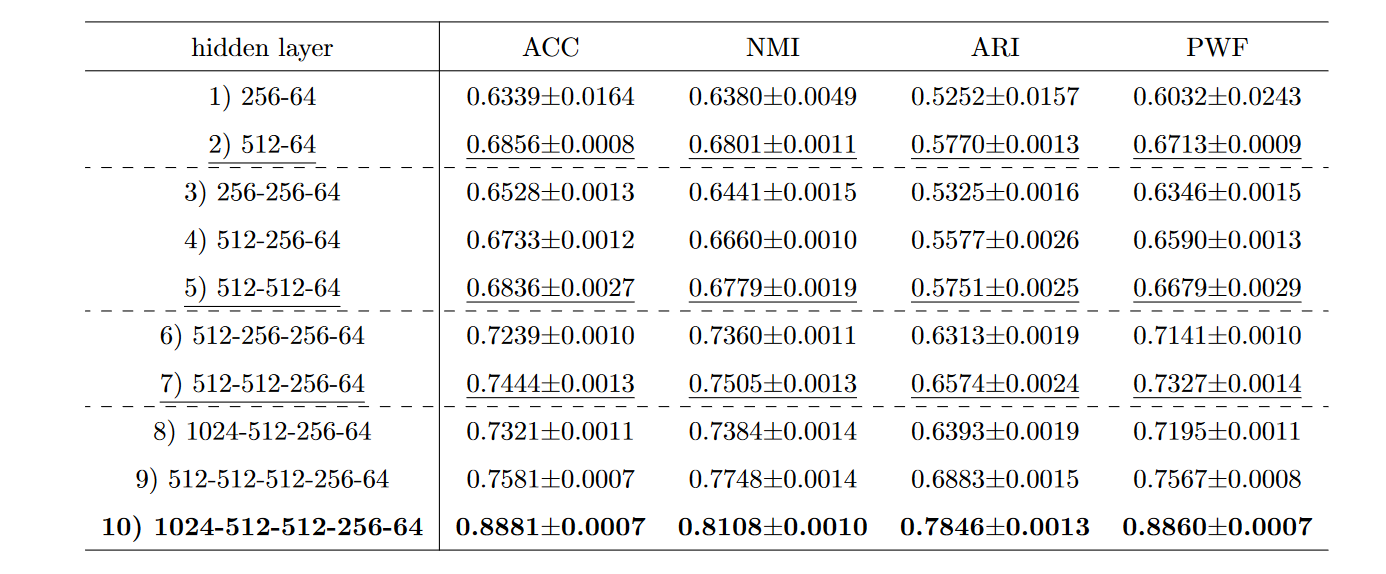
- 当我们设置相同的层数时，隐藏层的维度越大，聚类性能的提升就越显着****。这意味着更高的维度可以编码更多有用的信息，从而有利于联合优化**。
- 随着层数的增加，聚类性能稳步提高。在表 5 的结果中，案例 {1), 3), 6)} 和 {1), 4), 7), 9), 10)} 是明显的例子**
本文来自博客园，作者：我爱读论文，转载请注明原文链接：https://www.cnblogs.com/life1314/p/17461901.html
