Parallelly Adaptive Graph Convolutional Clustering ModelNetwork

论文阅读10-AGCC:Parallelly Adaptive Graph Convolutional Clustering Model

论文信息

论文地址：Parallelly Adaptive Graph Convolutional Clustering Model | IEEE Journals & Magazine | IEEE Xplore

代码地址：HeXiax/AGCC (github.com)

1.存在问题

1. 存在问题

GCN 的性能在很大程度上依赖于预训练图的质量，而图结构通常会被噪声或异常值破坏。

1. 同质性是图结构数据的一个重要特征，反映了图结构是否准确地描述了节点之间的关系。从非图结构数据中衍生出来的图结构来描述数据之间的关系是不准确的。另一方面，图结构数据中的自然图通常会被噪声和异常值破坏，例如相似节点之间缺失的边连接或不同节点之间错误添加的边。这种不准确的图结构为 GCN 中传递的消息提供了误导性信息，并降低了节点表示学习的性能。因此，如何将低同质性数据改进为高同质性数据具有挑战性
2. 鲁棒性：我们还观察到一个有趣的现象，即**基于图神经网络 (GNN) 的深度聚类方法在图结构数据上表现良好**，而**基于 AE 的深度聚类方法在非图结构数据上表现更好**。如何有效地利用这两种模式的优势是最终的挑战。

2. 解决问题

1. 如何解决

创新点：

1. 提出了一种名为AGCC的新型并行深度聚类方法，该方法主要由两个并行网络组成，即AGC网络和AE网络。
2. AGC网络被设计在深度聚类任务中，它交替地逐层更新图结构和数据表示，以提高原始图结构的质量并传播最优数据表示。这明显不同于SDCN中的固定图结构。
3. AMF模块旨在融合AGC和AE的优点，将注意力权重分配给异构表示，逐层学习综合融合表示，促进构建更好的相似图结构，同时缓解过平滑问题GCN。
4. 我们同时重构了样本和对应的图关系，主要是在潜在表示中包含更多的内容和结构信息。

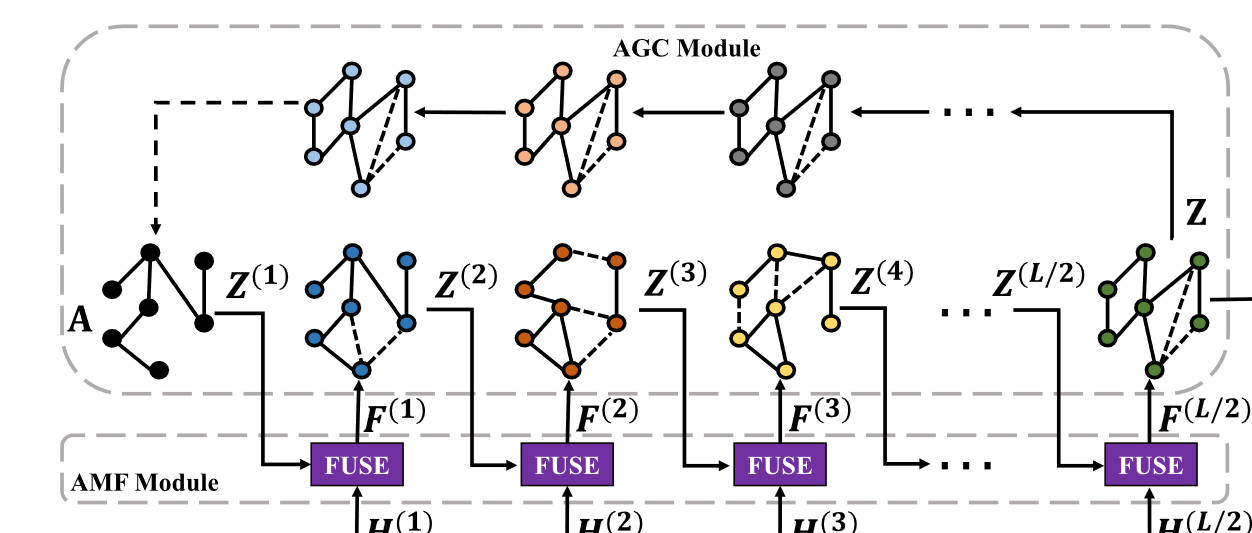
3.AGCC model

1. model structrue

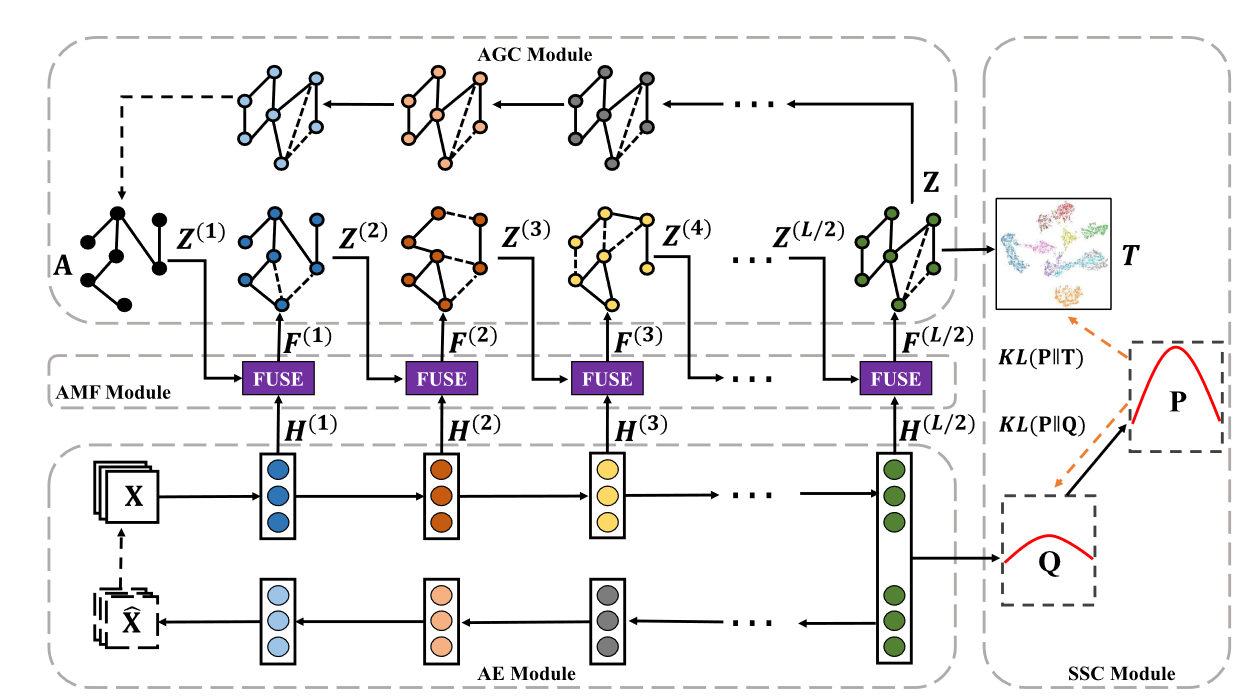
AGCC模型主要由4个模块组成：**AE模块、基于注意力机制的融合（AMF）模块、自适应图卷积（AGC）模块和SSC模块****。

1. AE模块：AE旨在从原始数据中提取有意义的节点表示。。

2. 自适应图卷积（AGC）模块： AGC 从融合表示中捕获节点之间的成对相关性以逐层更新图结构，然后借助上述更新的图结构聚合邻居节点特征

3. 基于注意力机制的融合（AMF）模块：AMF 学习它们的融合表示以包含节点本身及其邻居的信息。因此，通过这种综合融合表示重构的图结构可以更准确地描述样本之间的关系，引导AGC学习到更具判别力的节点表示

4. SSC模块：SSC 模块指导无监督学习中网络参数的优化过程

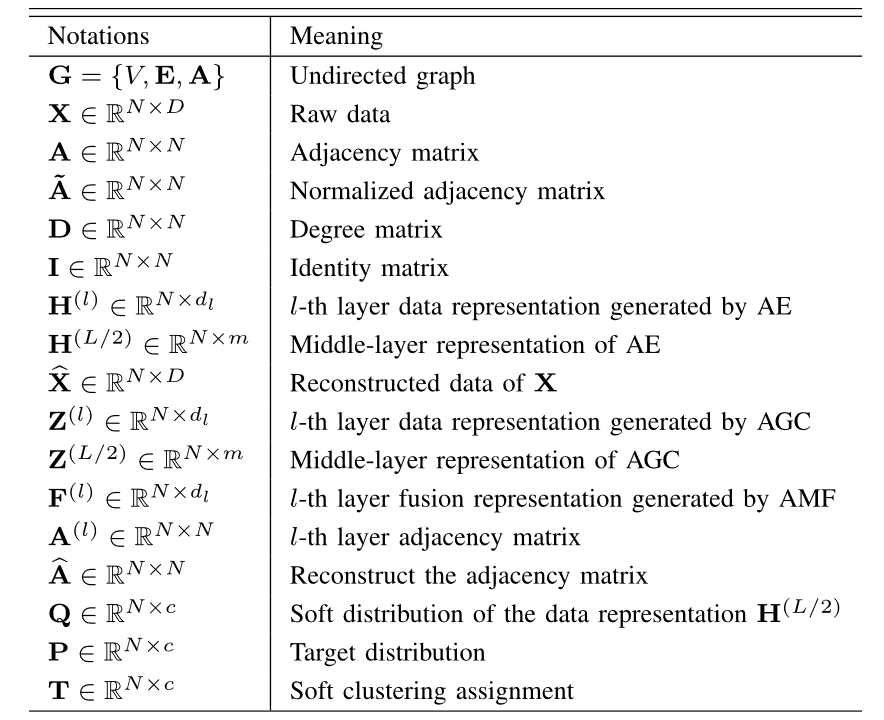
2.AE模块

编码器-解码器模块用于通过最小化原始数据和重建数据之间的重建损失来提取潜在表示。

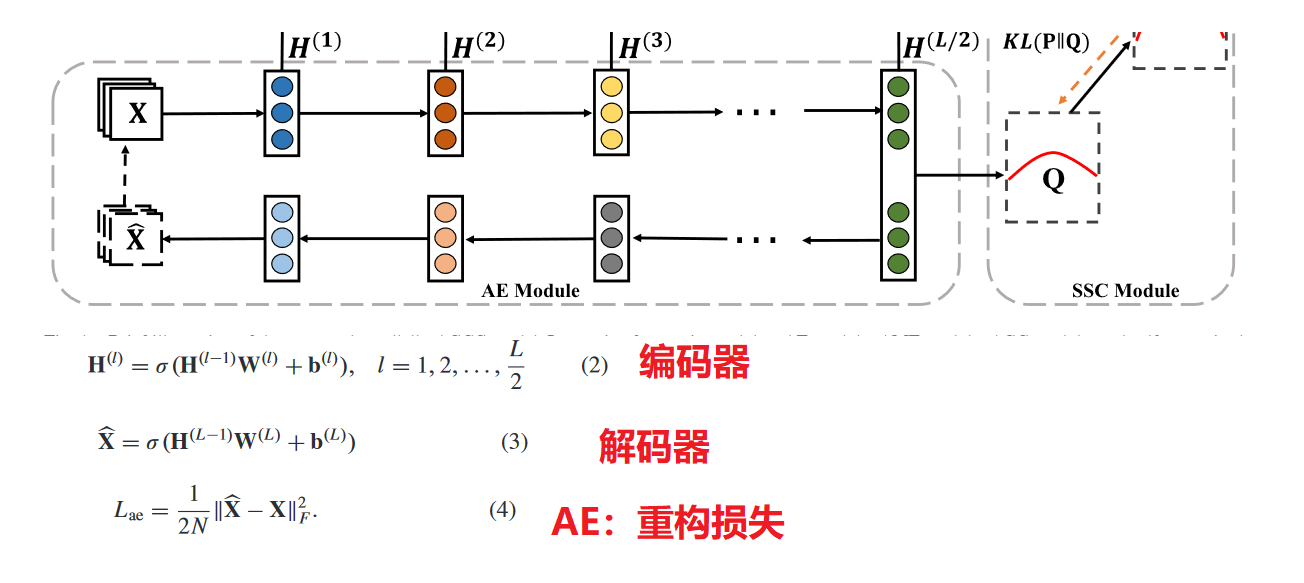
3.AMF融合模块

​ AE模块旨在从原始数据中提取抽象数据表示，而AGC模块借助更新的图结构聚合邻居节点特征，以学习更具辨别力的数据表示。这两个模块在某种意义上探索不同的特征，提取不同的信息。

​ **AMF模块来分别对AGC模块和AE模块学习到的数据表示进行逐层加权和融合**。通过这种方式，学习到的综合融合表示包含节点自身及其邻居的信息，从而构建了更好的相似性结构。

​

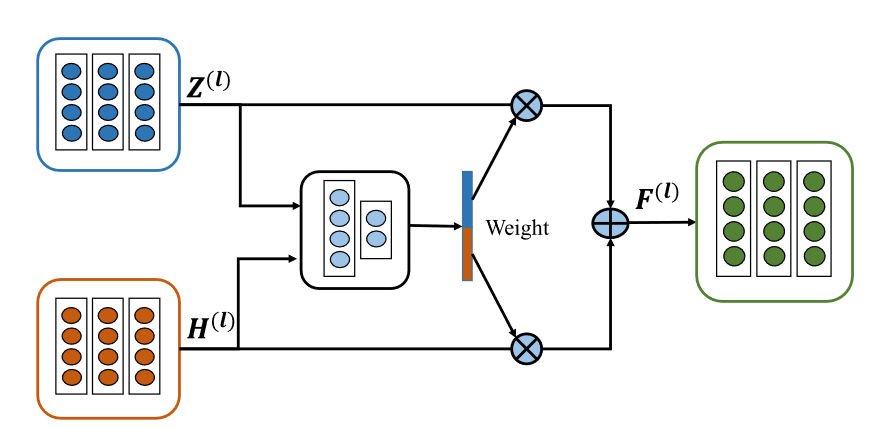
​ AMF 模块主要由三个全连接层和一个 softmax 层组成，旨在分配适当的AE 和 AGC 模块的学习数据表示的权重

​ 具体来说，对于第 l 层，我们将从 AE 模块学习的数据表示 H(l) ∈ RN×dl 和从 AGC 模块学习的相应数据表示 Z(l) ∈ RN×dl 通过以下方式连接起来：

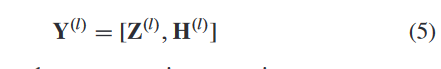
​ 利用连接的特征 Y(l)，我们根据相应的重要性学习 Z(l) 和 H(l) 的权重，并通过获得融合表示 F(l)

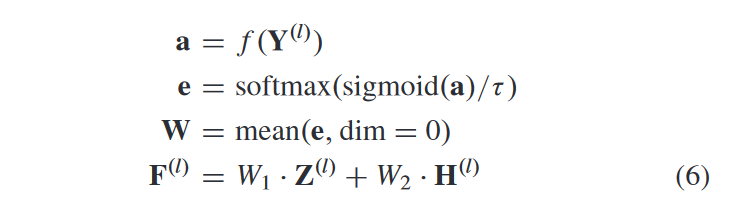
其中学习权重 W = [W1, W2]。另外，f(·)代表一个三层全连接网络，τ为校准因子。 sigmoid(·) 函数和校准因子可以被认为是一种技巧，可以避免将几乎“1”的分数分配给最相关的数据表示

4. AGC模块

现实世界中大多数通常被噪声和异常值破坏的图结构可能会为 GCN 中传递的消息提供误导性信息。传统的基于 GCN 的方法无法处理损坏的图结构，因为它们使用给定的固定图

具体来说，我们将融合表示 F(l) 发送到相应的 AGC 模块，数据的高阶结构信息可以通过自适应图卷积操作来捕获。同一簇中的节点应该具有相似的表示，由节点表示构建的相似图可以更好地描述节点之间的关系。为了获得第 l 层的自适应图，我们计算融合表示的内积以构造其邻接矩阵，如下所示

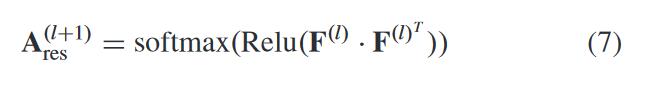
其中我们使用 softmax 函数生成归一化邻接矩阵 A(l+1) res ，这简化了计算。同时，原始邻接矩阵仍然包含很多有用的图结构信息，因此我们将学习到的自适应图A(l+1)res添加到原始图̃A中，更新图拓扑如下：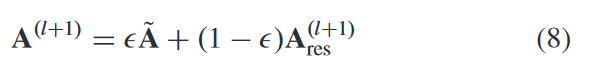

与传统的 GCN 相比**，所提出的 AGC 模块在优化过程中自适应地从融合表示 F(l) 中捕获节点之间的成对相关性，从而有效地减轻了图结构被噪声和异常值破坏的负面影响**。

AGC层级传播公式:

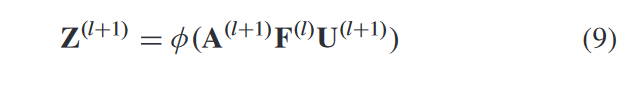
AGC第一层计算：

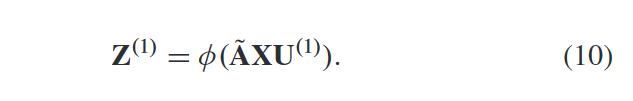
AGC损失计算：

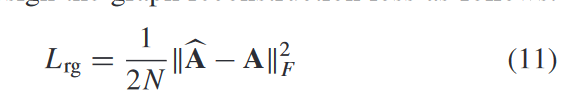
AGC重构邻接矩阵：

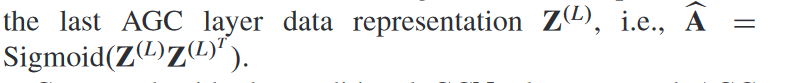
5. AGCC算法流程图

6.SSC 模块Self-Supervised Clustering Module

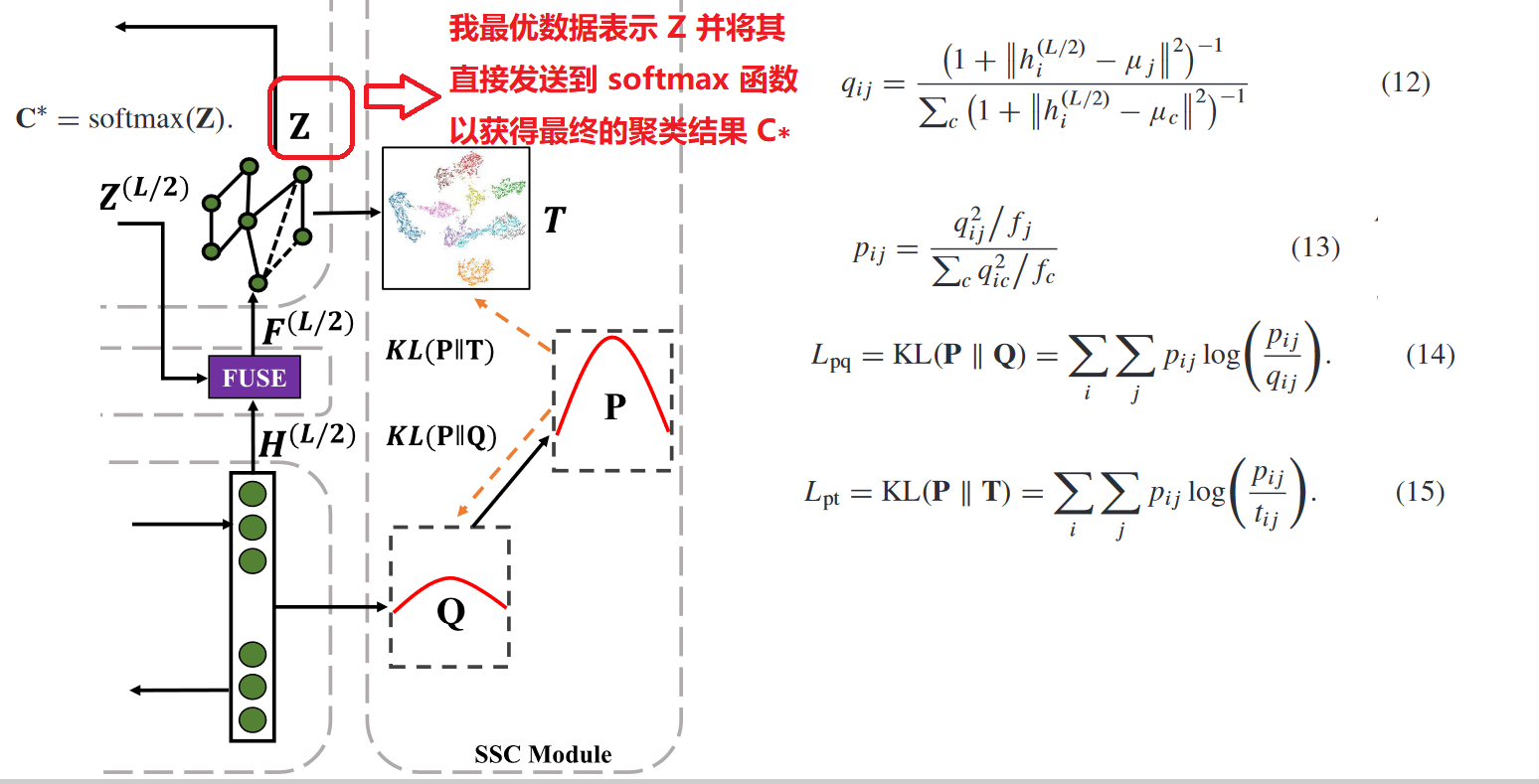
7.AGCC 代码

class AttentionLayer(nn.Module):
    def __init__(self, last_dim, n_num):
        super(AttentionLayer, self).__init__()
        self.n_num = n_num
        self.fc1 = nn.Linear(n_num * last_dim, 500)
        self.fc2 = nn.Linear(500, 100)
        self.fc3 = nn.Linear(100, n_num)
        self.attention = nn.Softmax(dim=1)
        self.relu = nn.ReLU()
        self.T = 10
        for m in self.modules():
            if isinstance(m, nn.Conv2d) or isinstance(m, nn.Linear):
                torch.nn.init.kaiming_normal_(m.weight)

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        x = self.relu(x)
        x = self.fc3(x)
        x = torch.sigmoid(x)
        attention_sample = self.attention(x / self.T)
        attention_view = torch.mean(attention_sample, dim=0, keepdim=True).squeeze()
        return attention_view

class FusionLayer(nn.Module):
    def __init__(self, last_dim, n_num=2):
        super(FusionLayer, self).__init__()
        self.n_num = n_num
        self.attentionLayer = AttentionLayer(last_dim, n_num)
    def forward(self, x, k):
        y = torch.cat((x, k), 1)
        weights = self.attentionLayer(y)
        x_TMP = weights[0] * x + weights[1] * k
        return x_TMP


def dot_product(z):
    if opt.args.name == "usps" or opt.args.name == "hhar" or opt.args.name == "reut":
        adj1 = F.softmax(F.relu(torch.mm(z, z.transpose(0, 1))), dim=1)
    else:
        adj1 = torch.sigmoid(torch.mm(z, z.transpose(0, 1)))
        adj1 = adj1.add(torch.eye(adj1.shape[0]).to(device))
        adj1 = normalize(adj1)
    return adj1

def normalize(mx):

    rowsum = mx.sum(1)
    r_inv_sqrt = torch.pow(rowsum, -0.5).flatten()
    r_inv_sqrt[torch.isinf(r_inv_sqrt)] = 0.
    r_mat_inv_sqrt = torch.diag(r_inv_sqrt)
    mx = torch.matmul(mx, r_mat_inv_sqrt)
    mx = torch.transpose(mx, 0, 1)
    mx = torch.matmul(mx, r_mat_inv_sqrt)
    return mx


class AE(nn.Module):

    def __init__(self, n_enc_1, n_enc_2, n_enc_3, n_dec_1, n_dec_2, n_dec_3,
                 n_input, n_z):
        super(AE, self).__init__()
        self.enc_1 = Linear(n_input, n_enc_1)
        self.enc_2 = Linear(n_enc_1, n_enc_2)
        self.enc_3 = Linear(n_enc_2, n_enc_3)
        self.z_layer = Linear(n_enc_3, n_z)

        self.dec_1 = Linear(n_z, n_dec_1)
        self.dec_2 = Linear(n_dec_1, n_dec_2)
        self.dec_3 = Linear(n_dec_2, n_dec_3)
        self.x_bar_layer = Linear(n_dec_3, n_input)

    def forward(self, x):
        enc_h1 = F.relu(self.enc_1(x))
        enc_h2 = F.relu(self.enc_2(enc_h1))
        enc_h3 = F.relu(self.enc_3(enc_h2))
        z = self.z_layer(enc_h3)

        dec_h1 = F.relu(self.dec_1(z))
        dec_h2 = F.relu(self.dec_2(dec_h1))
        dec_h3 = F.relu(self.dec_3(dec_h2))
        x_bar = self.x_bar_layer(dec_h3)

        return x_bar, enc_h1, enc_h2, enc_h3, z, dec_h1, dec_h2, dec_h3



class DTFU(nn.Module):

    def __init__(self, n_enc_1, n_enc_2, n_enc_3, n_dec_1, n_dec_2, n_dec_3,
                 n_input, n_z, n_clusters, v=1):
        super(DTFU, self).__init__()

        # autoencoder for intra information
        self.ael = AE(
            n_enc_1=n_enc_1,
            n_enc_2=n_enc_2,
            n_enc_3=n_enc_3,
            n_dec_1=n_dec_1,
            n_dec_2=n_dec_2,
            n_dec_3=n_dec_3,
            n_input=n_input,
            n_z=n_z)

        self.ael.load_state_dict(torch.load(opt.args.pretrain_path, map_location='cpu'))

        # GCN for inter information
        self.gnn_1 = GNNLayer(n_input, n_enc_1)
        self.gnn_2 = GNNLayer(n_enc_1, n_z)
        #self.gnn_2 = GNNLayer(n_enc_1, n_enc_2)
        self.gnn_3 = GNNLayer(n_enc_2, n_enc_3)
        self.gnn_4 = GNNLayer(n_enc_3, n_z)
        self.gnn_5 = GNNLayer(n_z, n_clusters)

        self.gnn_6 = GNNLayer(n_clusters, n_dec_1)
        self.gnn_7 = GNNLayer(n_dec_1, n_dec_2)
        self.gnn_8 = GNNLayer(n_dec_2, n_dec_3)
        self.gnn_9 = GNNLayer(n_dec_3, n_input)

        self.fuse1 = FusionLayer(n_enc_1)
        self.fuse2 = FusionLayer(n_enc_2)
        self.fuse3 = FusionLayer(n_enc_3)
        self.fuse4 = FusionLayer(n_z)

        self.fuse5 = FusionLayer(n_dec_1)
        self.fuse6 = FusionLayer(n_dec_2)
        self.fuse7 = FusionLayer(n_dec_3)


        # cluster layer
        self.cluster_layer = Parameter(torch.Tensor(n_clusters, n_z))
        torch.nn.init.xavier_normal_(self.cluster_layer.data)

        # degree
        self.v = v

    def forward(self, x, adj):
        # DNN Module
        x_bar, tra1, tra2, tra3, z, dec_1, dec_2, dec_3 = self.ael(x)

        sigma = 0.5

        #GCN Module
        h = self.gnn_1(x, adj)

        h = self.fuse1(h, tra1)
        adj1 = dot_product(h)
        h = self.gnn_2(h, ((1 - sigma) * adj1 + sigma * adj))

        # h = self.fuse2(h, tra2)
        # adj1 = dot_product(tra2)
        # h = self.gnn_3(h, ((1 - sigma) * adj1 + sigma * adj))
        #
        # adj1 = dot_product(h)
        # h = self.fuse3(h, tra3)
        # h = self.gnn_4(h, ((1 - sigma) * adj1 + sigma * adj))

        h = self.fuse4(h, z)
        adj1 = dot_product(h)
        h1 = self.gnn_5(h, ((1 - sigma) * adj1 + sigma * adj), active=False)


        predict = F.softmax(h1, dim=1)


        h = self.gnn_6(h1, ((1 - sigma) * adj1 + sigma * adj))
        h = self.fuse5(h, dec_1)
        h = self.gnn_7(h, ((1 - sigma) * adj1 + sigma * adj))
        h = self.fuse6(h, dec_2)
        h = self.gnn_9(h, ((1 - sigma) * adj1 + sigma * adj))

        A_pred = dot_product(h)



        # Dual Self-supervised Module
        q = 1.0 / (1.0 + torch.sum(torch.pow(z.unsqueeze(1) - self.cluster_layer, 2), 2) / self.v)
        q = q.pow((self.v + 1.0) / 2.0)
        q = (q.t() / torch.sum(q, 1)).t()

        return x_bar, q, predict, z, A_pred

4. result Analysis

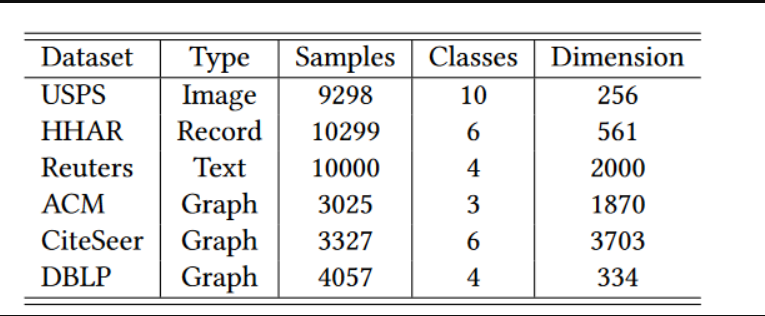
1. 数据集

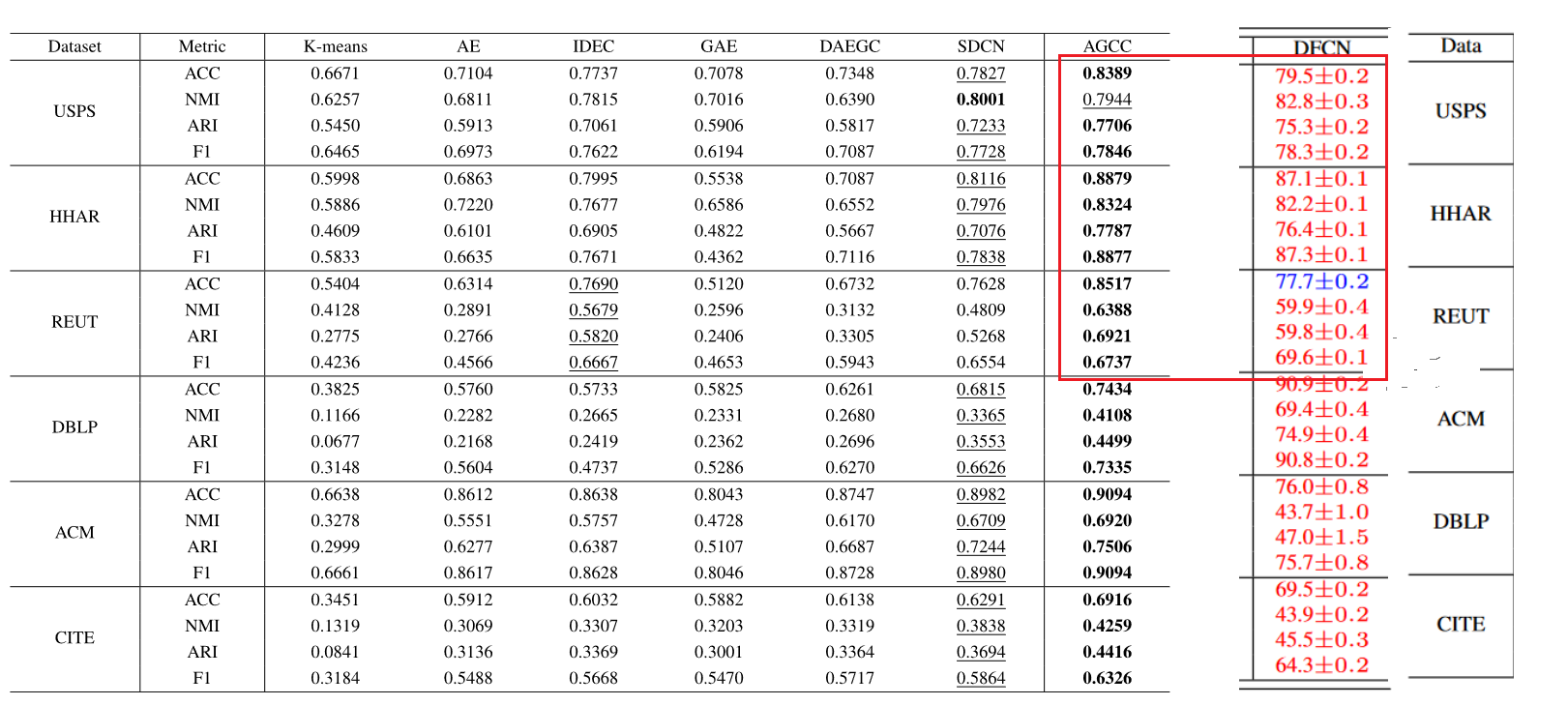
2. 实验结果

3.实验结果分析

1. 基于AE的深度聚类模型AE和IDEC，IDEC在AE的基础上增加了自监督模块。与AE相比，IDEC的聚类性能在6个数据集上都有显着提升，充分证明了自监督模块对提高聚类性能的重要性。然后，我们观察到在大多数情况下，SDCN 和我们的 AGCC 的聚类性能明显优于 IDEC。我们认为基于AE的深度聚类模型仅仅利用了数据的属性信息，而忽略了数据之间的相互联系关系，从而导致性能不佳。 GCN 可以弥补这个缺点。基于 GCN 的深度聚类模型 GAE 和 DAEGC 在所有数据集上的表现都比 SDCN 和 AGCC 差。我们认为，这些基于 GCN 的深度聚类模型仅仅利用了数据之间的结构信息，而没有充分考虑数据本身的属性信息。此外，多层图卷积的堆叠往往会导致过度平滑的问题。
2. 一个有趣的现象。对于直接提供数据图的数据集 DBLP、ACM 和 CITE，DAEGC 的聚类性能优于 IDEC。****对于没有提供相应图的数据集USPS、HHAR和REUT，GAE和DAEGC的聚类性能不如AE和IDEC。由于K近邻构建的图不能准确描述数据之间的关系，导致GAE和DAEGC的聚类性能较差。**因此，一个好的自适应图学习策略是必要的。
3. SDCN在图卷积过程中使用了固定的图结构。我们 AGCC 中不断更新的图表可以更好地反映数据之间的连接关系。此外，AGCC 提出了 AMF 模块来融合数据之间的结构信息和属性信息，充分利用了关键数据信息并解决了过度平滑问题。

4. 消融实验:ablation

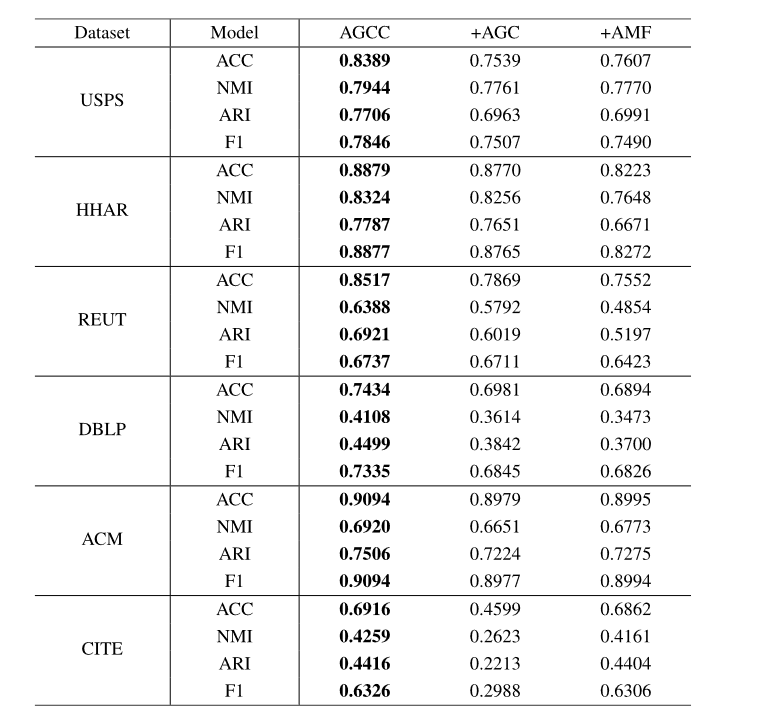
1. +AGC：通过简单的加法运算融合了从AE和AGC模块学习到的数据表示，替代了AGCC中的AMF模
2. +AMF：与固定图进行图卷积，提取数据的结构信息，替代了AGCC中的自适应图。

1. 结果分析

​ AGCC的聚类性能也优于+AMF，因为+AMF中的图在整个图卷积过程中是固定的。固定图的图卷积操作无法处理损坏的图结构。此外，与在携带数据间关联信息的DBLP、ACM、CITE数据集上的结果相比，+AMF在USPS、HHAR、REUT数据集上的聚类性能下降更为剧烈。由于这些数据集（USPS、HHAR 和 REUT）的初始图结构是以无监督方式构建的，因此图可能包含噪声和异常值，破坏了数据局部结构信息的完整性，进一步损害了聚类性能。值得注意的是，从 AE 模块学习到的数据表示包含了原始数据中最重要的属性信息，因此所提出的自适应更新每个网络层中的图拓扑结构的方法可以有效地解决这个问题。

​ AGC 模块从融合表示中捕获节点之间的成对相关性，以逐层更新图结构，其中融合表示集成了 AE 和 AGC 模块学习的数据表示。为了获得这种融合表示，简单地添加 AE 和 AGC 模块学习的数据表示不能充分利用这两个模块的优势，这会降低融合表示的性能，也会损害更新图结构的质量。 AMF 模块自然是为了缓解这个问题而设计的，通过将注意力权重分配给异构表示并促进构建良好的图结构。

5.AMF权重可视化

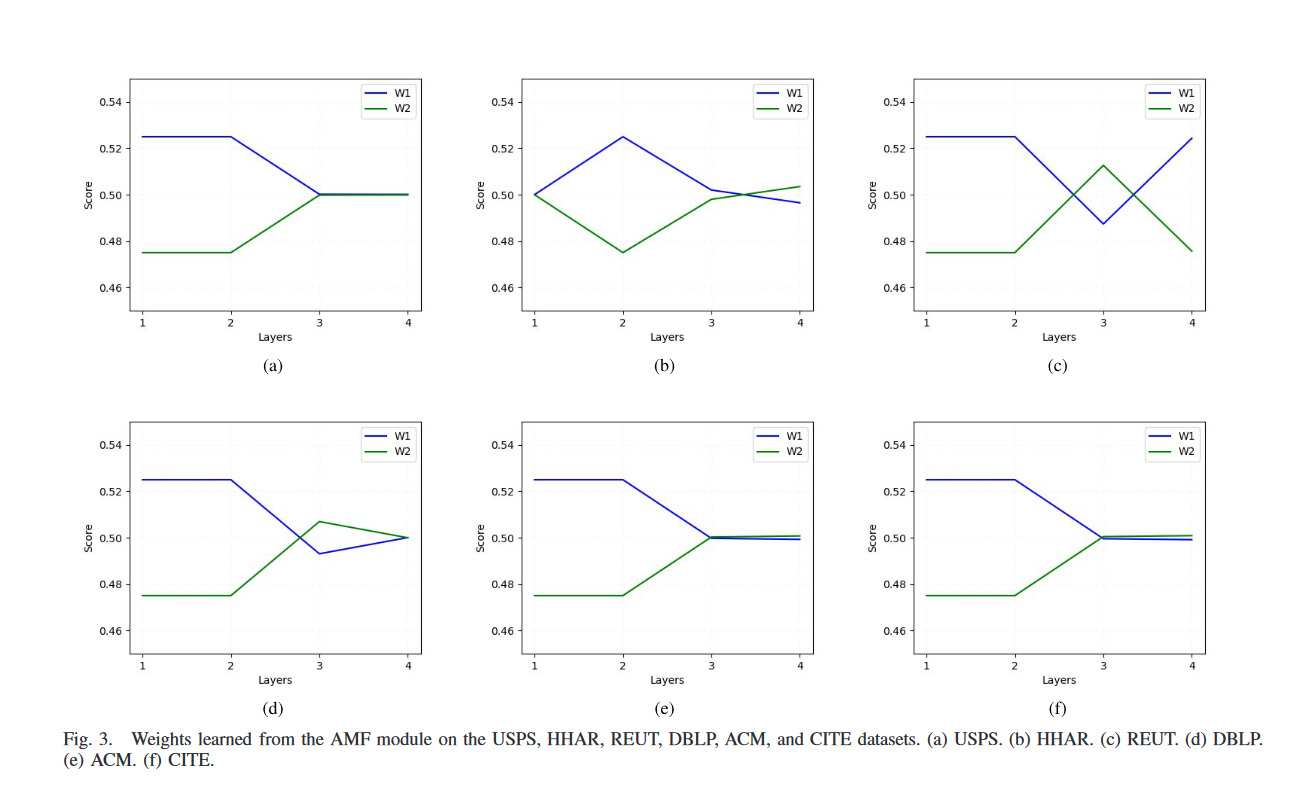
AGC 和 AE 模块在不同传播层学习到的数据表示既包含显着不同的信息，也包含大量重叠信息。我们提出的 AMF 模块可以自适应地为具有不同结构的数据表示分配适当的权重，以便它们可以相互补充以学习更有意义的数据表示。

​ 从图3可以看出，在大多数情况下，编码器部分的AGC模块学习到的数据表示的权重因子较大，而编码器部分的权重因子逐渐趋于均等。这意味着前两层不同模块学习到的数据表示是完全不同的，而AGC模块学习到的信息更为关键，因为它具有强大的捕获数据结构信息的能力。

---