Multi-View Attribute Graph Convolution Networks for Clustering
论文阅读04-Multi-View Attribute Graph Convolution Networks for Clustering:MAGCN
论文信息
论文地址:Multi-View Attribute Graph Convolution Networks for Clustering | IJCAI
论文代码:MAGCN
1.多视图属性聚类:MAGCN
1.存在问题:GNN 融入Multi-View Graph
1)他们不能将指定学习的不同权重的分配给邻域内的不同节点;
2)他们可能忽略了进行节点属性和图结构的重构以提高鲁棒性;
3)对于不同视图之间的一致性关系,没有明确考虑相似距离度量。
2.解决问题:MAGCN
本论文提出了一种新的多视图属性图卷积网络,用于聚类(MAGCN)多视图属性的图结构数据
-
为了将可
学习的权重分配给不同的节点,MAGCN开发了具有注意机制的多视图属性图卷积编码器,用于从多视图图数据中学习图嵌入。 -
属性和图重建均由 MAGCN 的图卷积解码器计算。 -
将
多视图图数据之间的几何关系和概率分布一致性纳入MAGCN的一致嵌入编码器中,以进一步促进聚类任务。
编码器1:
开发多视图属性图注意力网络以减少噪声/冗余并学习多视图图数据的图嵌入特征。
编码器2:
开发一致的嵌入编码器来捕获不同视图之间的几何关系和概率分布的一致性,从而自适应地为多视图属性找到一致的聚类嵌入空间。
2.MAGCN模型创新点
- 我们提出了一种新的多视图属性图卷积网络,用于对多视图属性的图结构数据进行聚类。:
为不同的邻域节点分配不同的权重 - 我们开发了具有注意机制的多视图属性图卷积编码器,以减少多视图图数据的噪声/冗余。
- 此外,还考虑了节点属性和图结构的重构以提高鲁棒性。:
重构节点信息和结构信息提高模型鲁棒性一致性嵌入编码器旨在通过探索不同视图的几何关系和概率分布一致性来提取多个视图之间的一致性信息。:多视图聚类特点应用
3.MAGCN 模型
1.MAGCN 先验知识
- MAGCN的编码器
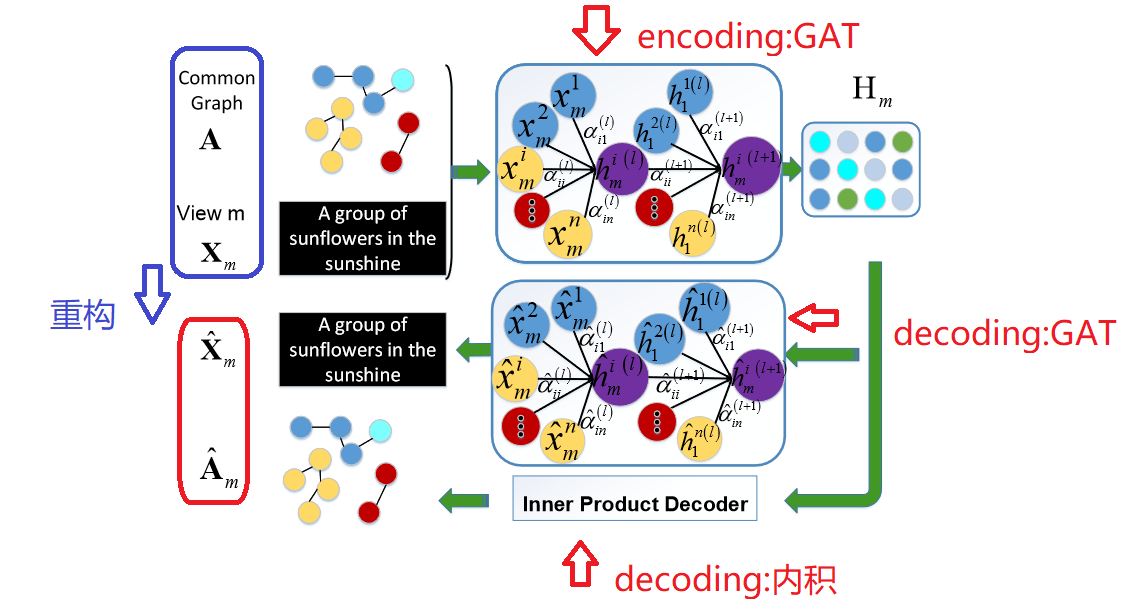
这个X 特征重构中GAT来自于:[1905.10715] Graph Attention Auto-Encoders (arxiv.org)
- GAT 和GATE 的区别
GATE:1905.10715] Graph Attention Auto-Encoders (arxiv.org)
GAT: 1710.10903] Graph Attention Networks (arxiv.org)
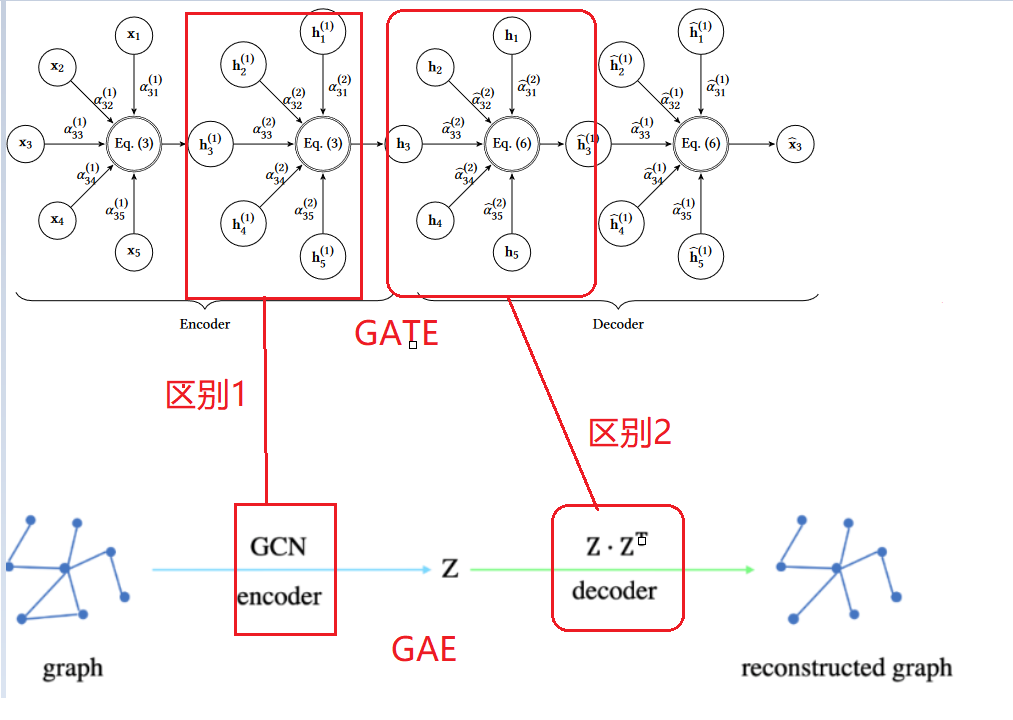

- GATE 和GAT 区别
GATE:1905.10715] Graph Attention Auto-Encoders (arxiv.org)
GAT: 1710.10903] Graph Attention Networks (arxiv.org)
GATE 的主要贡献是逆转编码过程,以便在没有任何监督的情况下学习节点表示。为此,我们使用与编码器层数相同的解码器。每个解码器层都试图反转其相应编码器层的过程
GATE 中编码器:使用的就是GAT 的共享参数机制,几乎是一样。
区别一激活函数:
GATE中采用的sigmoid的激活函数,GAT中采用的是LeajyReLU的函数,
区别二 激活函数的位置:
GATE和GAT激活函数在层级传播公式,激活顺序不一样
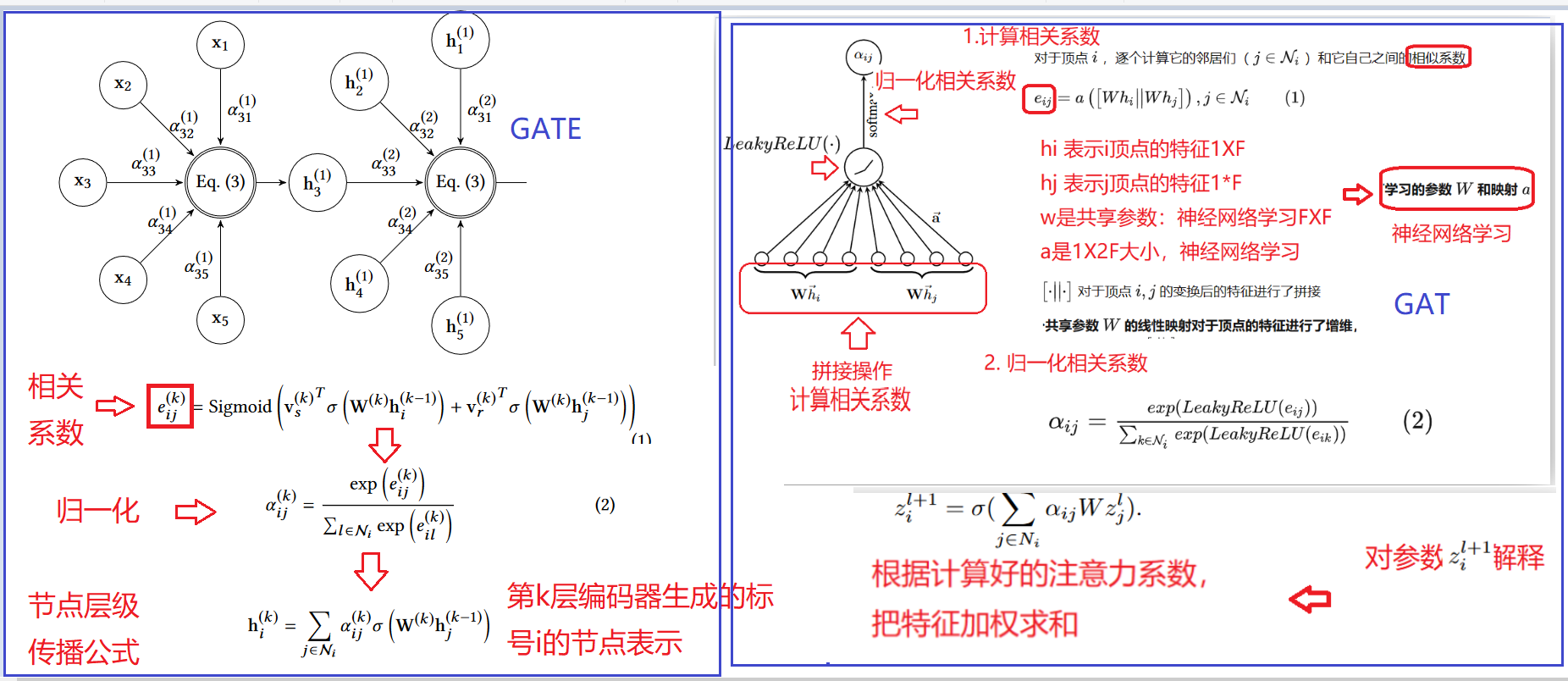
GATE中的解码器:
每个解码器层根据节点的相关性利用其邻居的表示来重建节点的表示

简化公式
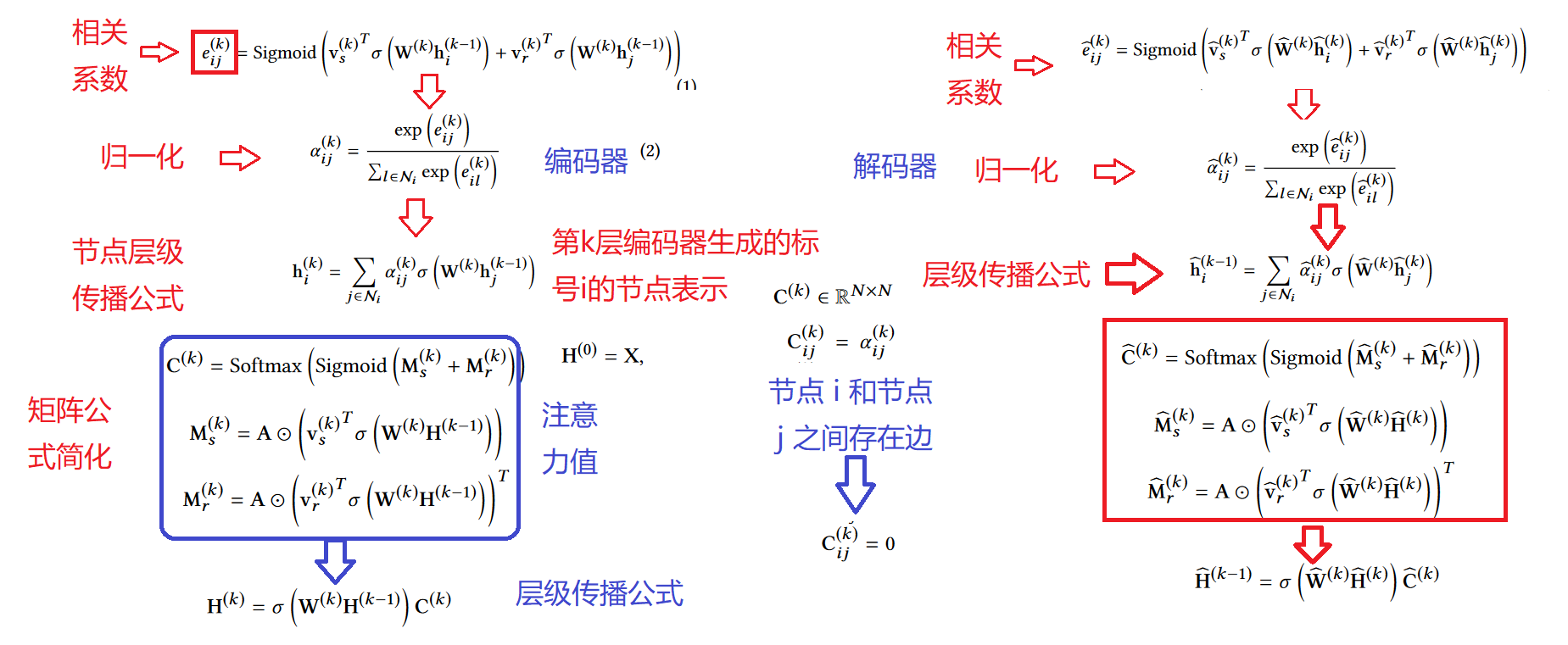
- GATE 步骤流程

- 图中参数

2.模型架构图
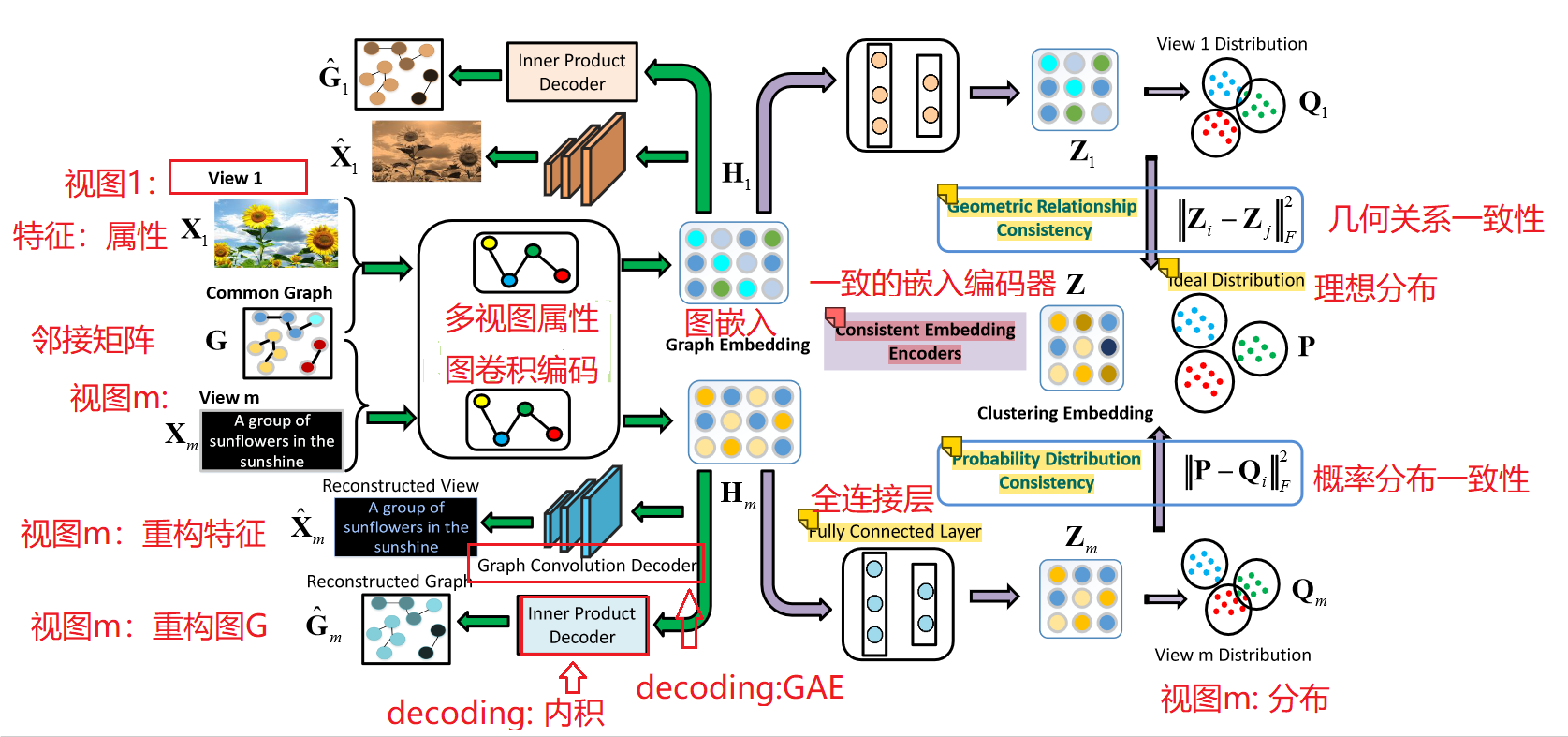
MAGCN模型主要有两个编码器组成:多视图属性图卷积编码器和一致嵌入编码器
用于聚类的多视图属性图卷积网络 (MAGCN) 的框架。
- 具有注意机制的多视图属性图卷积编码器:它们用于
从节点属性和图数据(图结构)中学习图嵌入。执行属性和图形重建以进行端到端学习。
- 一致嵌入编码器(Consistent embedding encoders):通过
几何关系和概率分布的一致性,进一步在多个视图之间获得一致的聚类嵌入。
MAGCN 模型训练过程:
我们首先将多视图图数据 Xm,通过多视图属性图卷积编码器 编码为图嵌入。将 Hm 馈入一致的嵌入编码器并获得一致的聚类嵌入 Z。聚类过程最终在由 Z 计算出的理想嵌入内在描述空间上进行。
3. MAGCN 模块详细
1. 多视图属性图卷积编码器:Multi-view Attribute Graph Convolution Encoder
- 主要作用
在多视图属性图卷积编码器中,第一个编码器将多视图节点属性矩阵和图结构映射到图嵌入空间。

- 编码器:encoding
为了更好的为自身节点和邻域节点分配可学习的权重,在节点之间使用了带有共享参数的注意力机制:GAT。:采用GCN+Attention的机制对各个view下的特征信息进行聚合,并得到各自的embedding
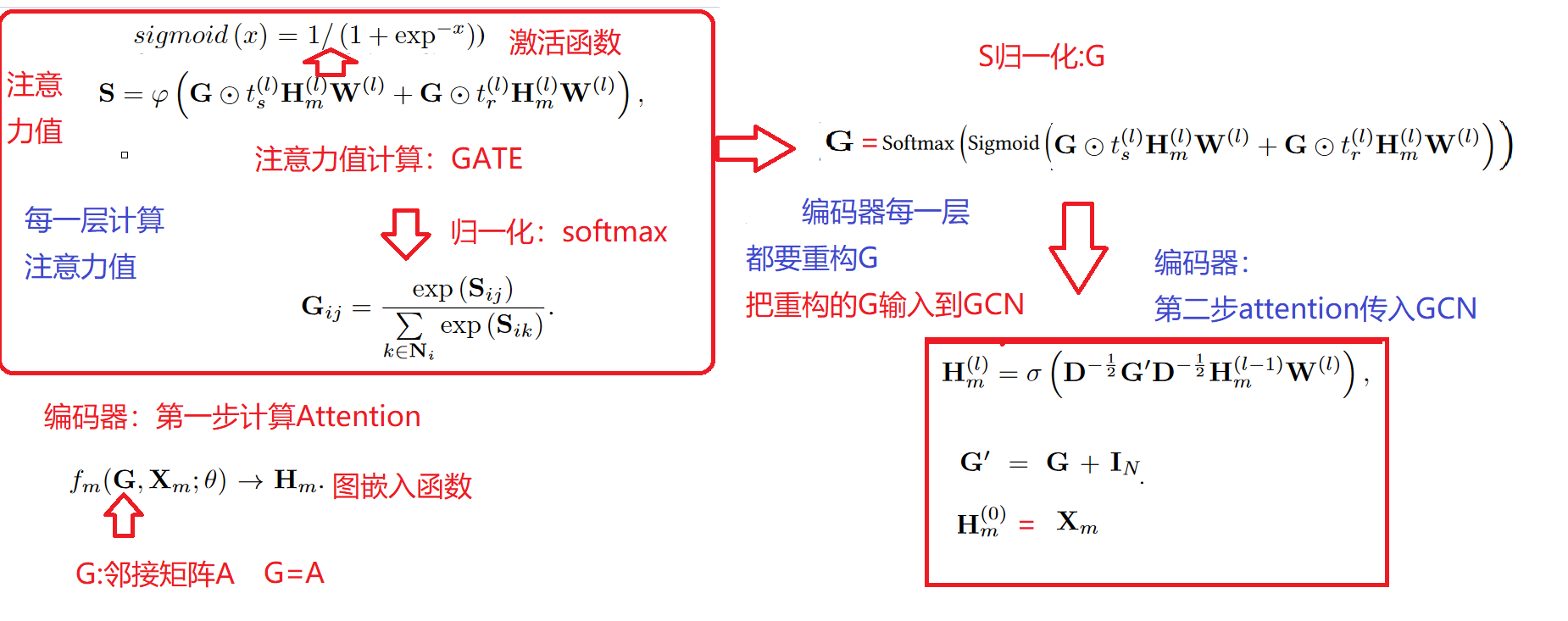
在每一次用GCN进行特征聚合之前,先要按照这个attention机制求得attention矩阵,然后将其作为G GG输入到GCN框架中.
- 解码器:decoding

- 损失函数
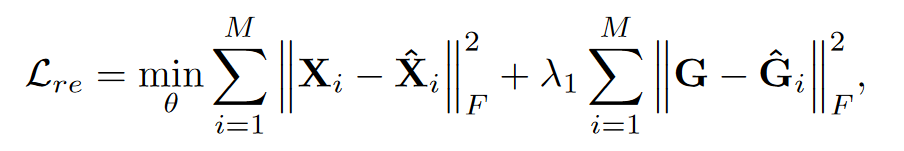
比较decoding的结果与最初的X 是否逼近(这是指特征信息的逼近),G 的逼近,越逼近说明网络中encoding和decoding过程中没有损失太多的信息
M :表示视图的个数,因此需要把每一个视图重构出来的损失相加和
2.一致嵌入编码器:Consistent embedding encoders
1. 几何关系一致性
- 几何关系一致性目的
目的:让各个视图(view)下得到的Zm 去互相逼近,越逼近说明在各个view下得到的Z m 比较一致,进一步说明了网络学到的都是主要信息(因此才能保证各个view下的Zm都很逼近)
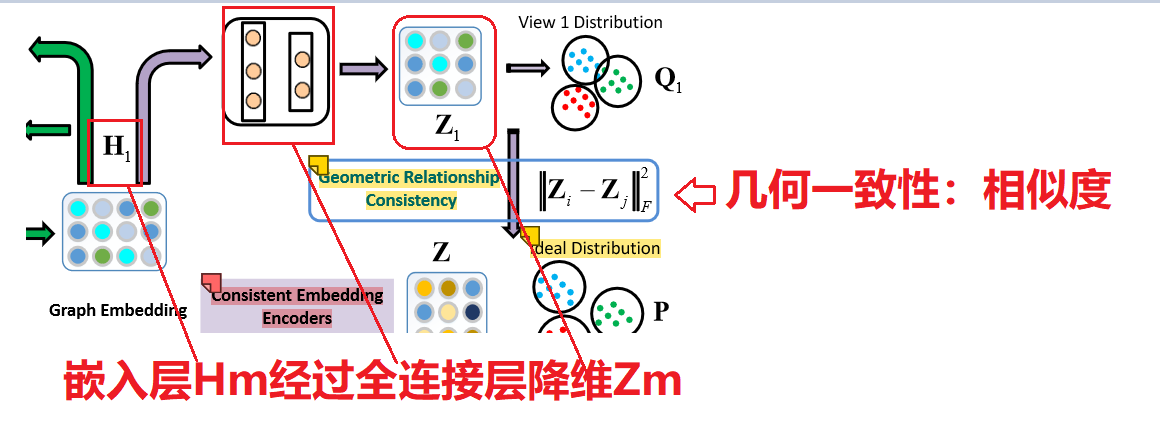
- 几何关系一致性步骤
步骤:
- 降维 :Zm包含了几乎所有的原始信息,不适合直接进行多视图融合。使用一致的聚类层来学习一个由所有 Zm 自适应集成的公共聚类嵌入 Hm。:
Hm被映射到低维空间Zm中。 - 计算几何相似度:假设
Zm 和 Zb 是从一致嵌入编码器获得的视图 m 和 b 的低维空间特征矩阵。然后我们可以使用它们来计算几何关系相似度。比如:曼哈顿距离,欧氏距离,余弦相似度。
- 损失函数
几何关系一致性损失函数:
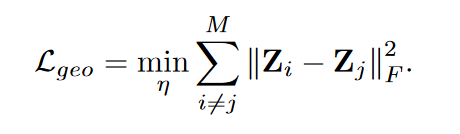
2. 概率分布的一致性
- 概率分布一致性 目的
目的:
各个view下得到的概率分布矩阵都与总的概率分布矩阵去进行逼近,越逼近说明每个view下得到的概率分布矩阵都是比较好的,从而也说明了网络确实具有较好的鲁棒性
- 概率分布一致性
我们还考虑了公共表示 Z 和每个视图的潜在表示 Zm 之间概率分布的一致性.

对于 i 样本和 j 样本,我们使用 Student 的 t 分布作为核心来度量嵌入点 hi 和聚类中心向量 μj 之间的相似性,如下所示:
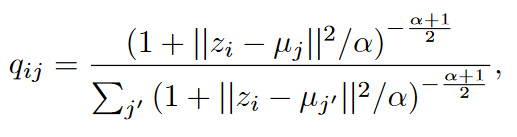
qij可以看作是将样本i分配给聚类j的概率,即软分配。
*qiu*表示节点i属于簇u的概率,将其看作是每个节点的软聚类分配标签,如果值越大,那么可信度越高 。通过平方运算将这种可信度放大:
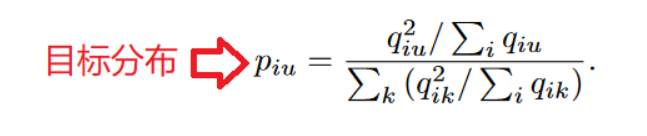
- 损失函数
MAGCN论文的损失函数没有采用KL散度
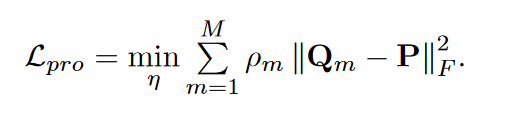
3. 总损失函数
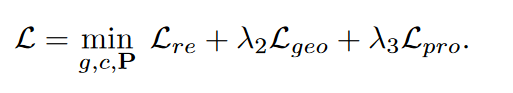
我们根据辅助分布P预测每个节点的簇。对于节点i,它的簇可以用pi计算,其中概率值最高的索引是i的簇。因此我们可以得到节点 i 的簇标签为:
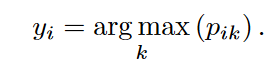
4. 实验结果分析
1. MAGCN实验
- 数据 集
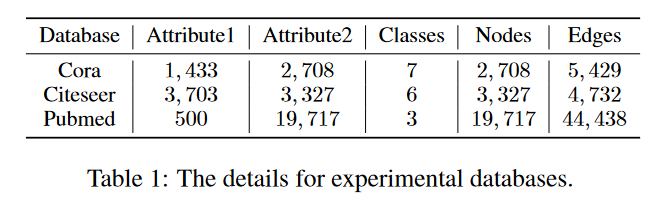
- 多视图的构建
一般的图结构数据库包含一个图和一个属性,目前还没有真正的具有多视图属性的图结构数据。
图结构数据的属性为0, 1,它们是离散结构的也是片面描述的。为了更丰富地描述图结构,我们通过改变其操作使属性连续。
受多图的启发,它自己构造另一个图,我们通过原始属性构造额外的属性视图。我们使用快速傅立叶变换 (FFT)、Gabor 变换、欧拉变换和笛卡尔积在视图 1 的基础上构建视图 2:
视图 2 由笛卡尔积构成
- 实验参数
我们为所有三个数据库使用了两层多视图属性图卷积编码器,在多视图图卷积自动编码器中使用非线性激活函数作为 Relu 函数。
| 数据集 | Cora | citeseer | pubmed |
|---|---|---|---|
| 维度 | 512*512 | 2000*512 | 128 *64 |
- 实验结果
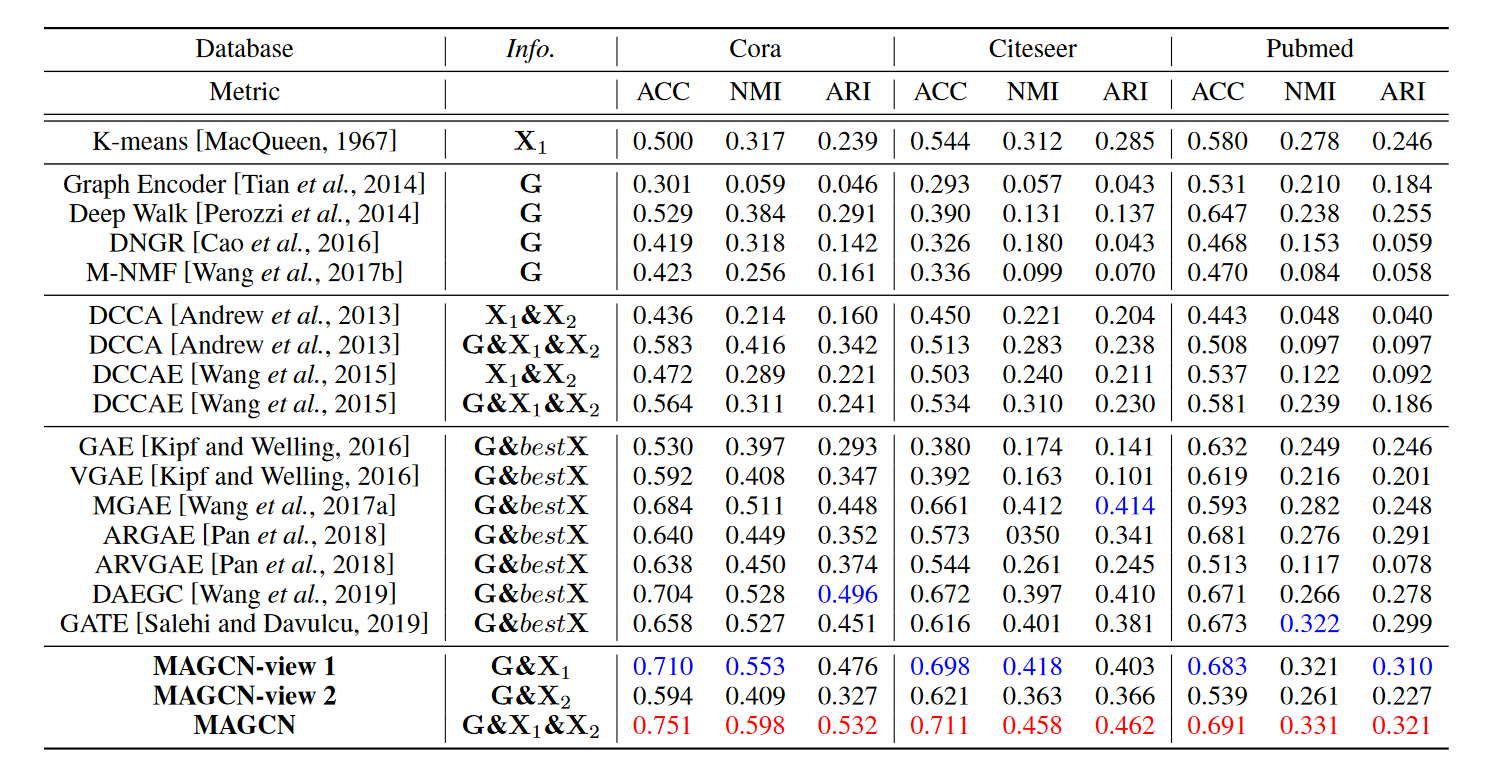
-
MAGCN 在 Cora 和 Citeseer 上比单一视图的 GCN 提高了 5% 以上,在 Pubmed 上提高了 1% 以上,这表明以
几何关系和概率分布的一致性来整合不同的视图是有效的。 -
单视图图卷积聚类方法:DAEGC 和 GATE,具有相对更好的聚类性能,这表明注意机制根据可训练的注意力权重聚合邻域信息有助于提高聚类性能. -
深度多视图聚类方法通过使用图结构信息获得更好的性能。这表明图结构信息可以对聚类做出有益贡献
2. MAGCN 消融实验
- 概率分布一致性分析
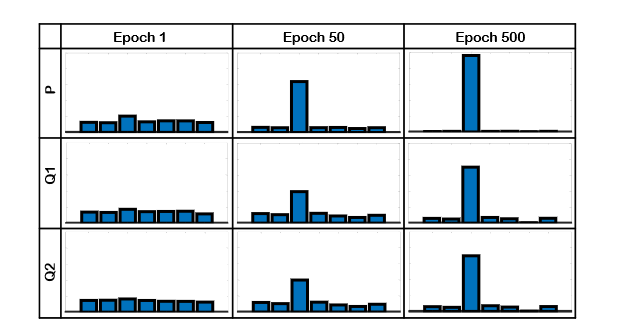
-
在初始迭代中,
随机初始化使得每个类别的概率基本相似,无法找出样本属于哪个类别。 -
在第三类中的概率随着迭代次数的增加而增加,
Z、Z1、Z2上的概率分布趋于一致,说明理想的多视角描述特征Z是逐渐学习到的.

- 参数的影响
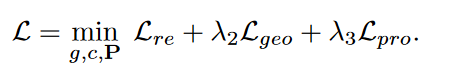
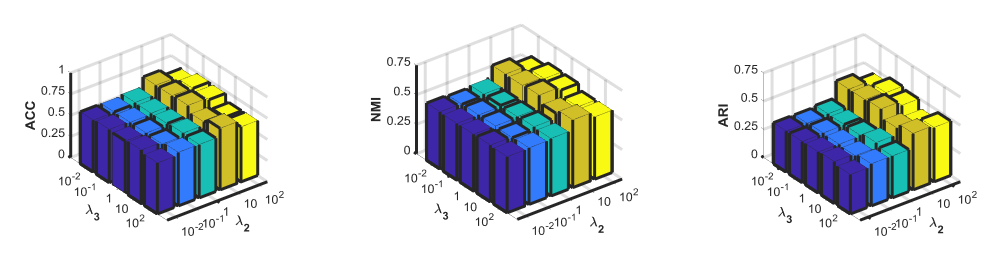
对geo 和pro 的超参数分析:
我们保持reconstruction loss的正则参数1不变,改变模型中几何关系一致性和概率分布一致性的正则参数2和3。
- 不同视图view2构造方法分析
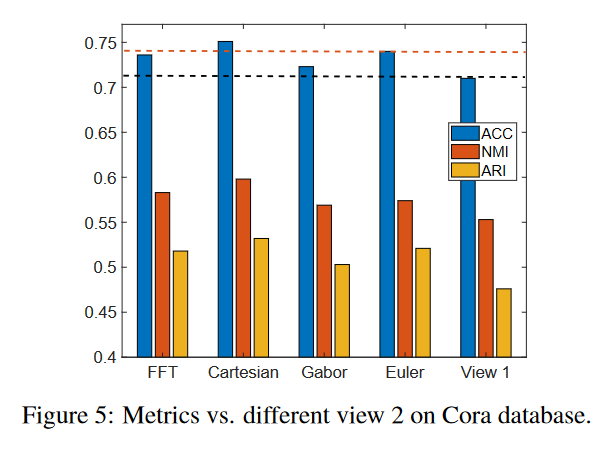
- 对于所有类型的视图 2,
两个视图的聚类结果优于单个视图 1(用黑线标记)的情况。 - 对于视图 2(红线标记),
笛卡尔积方式比其他构造方式效果更好。
4.参考链接
论文学习--Multi-View Attribute Graph Convolution Networks for Clustering(MAGCN)_爱啊岛呀~的博客-CSDN博客
t-student 分布推导过程:关于“Unsupervised Deep Embedding for Clustering Analysis”的优化问题 - 凯鲁嘎吉 - 博客园 (cnblogs.com)
消融实验:https://blog.csdn.net/weixin_44065652/article/details/123527844
本文来自博客园,作者:我爱读论文,转载请注明原文链接:https://www.cnblogs.com/life1314/p/17323778.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通