Deep graph clustering with enhanced feature representations for community detection

论文阅读03-EFR-DGC:Enhanced Feature Representations for Deep Graph Clustering

论文信息

论文地址：Deep graph clustering with enhanced feature representations for community detection | SpringerLink

论文代码：https://github.com/grcai/DGC-EFR

1.存在问题

1. DAEGC在处理拓扑关系 方面取得了成功，但深度图聚类通常无法充分学习节点的属性信息。 节点特征信息学习不足。======图模型通常更关注拓扑信息而忽略节点属性的重要性。

​ DAEGC 这篇论文中证明了：图注意力网络构建图自动编码器，作为更强大的学习者来提取足够的拓扑信息进行聚类：EFR-DGC 拓扑关系（结构信息）： 通过利用DAEGC 中的图注意力机制的编码器，来处理拓扑关系和属性信息融合。

2. 结构深度聚类网络（SDCN）和深度融合聚类网络（DFCN）将节点的结构信息整合到深度聚类中,图模型的能力有限以及缺乏足够的模型优化自监督信息，这两者仍然存在特征表示不足的问题：

​ SDCN这篇论文中证明了：自动编码器，作为来学习层次的属性关系。EFR-DGC 属性关系（节点特征信息）： 通过利用SDCN 中的AE编码器，来学习层次的属性关系。

2.EFR-DGC解决问题

提出一种改进的特征表示方法，用于发现社区中的深度图聚类。

1. 首先构造一个具有多个全连接层的基本自动编码器 (AE)来学习层次属性信息，
2. 然后将AE学习到的属性信息，其传递给图自动编码器（GAE）的神经层。图自编码器接收到的分层属性信息与其提取的拓扑关系有机地组合，以生成用于聚类的增强的特征表示。
3. 其次，设计了一自监督机制来优化深度图聚类模型，该机制利用两个自动编码器的重构损失和聚类损失作为自监督信息，有效地指导模型更新。这样克服了生成表示中属性信息不足的问题，从而更有利于社区发现。

优点长处：

与 SDCN 和 DFCN 中使用的简单图卷积网络相比，我们的图自动编码器能够通过为相邻节点分配不同的权重来很好地处理它们的属性和拓扑信息

3.模型

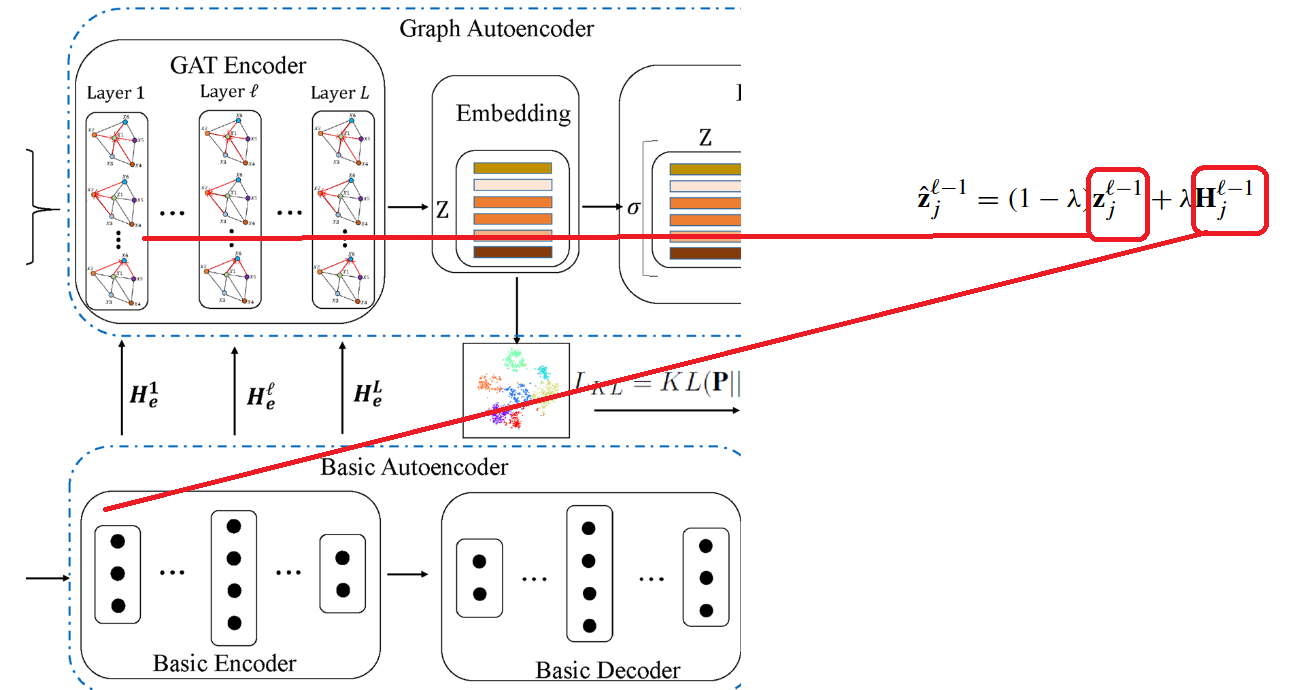
1. 模型架构图

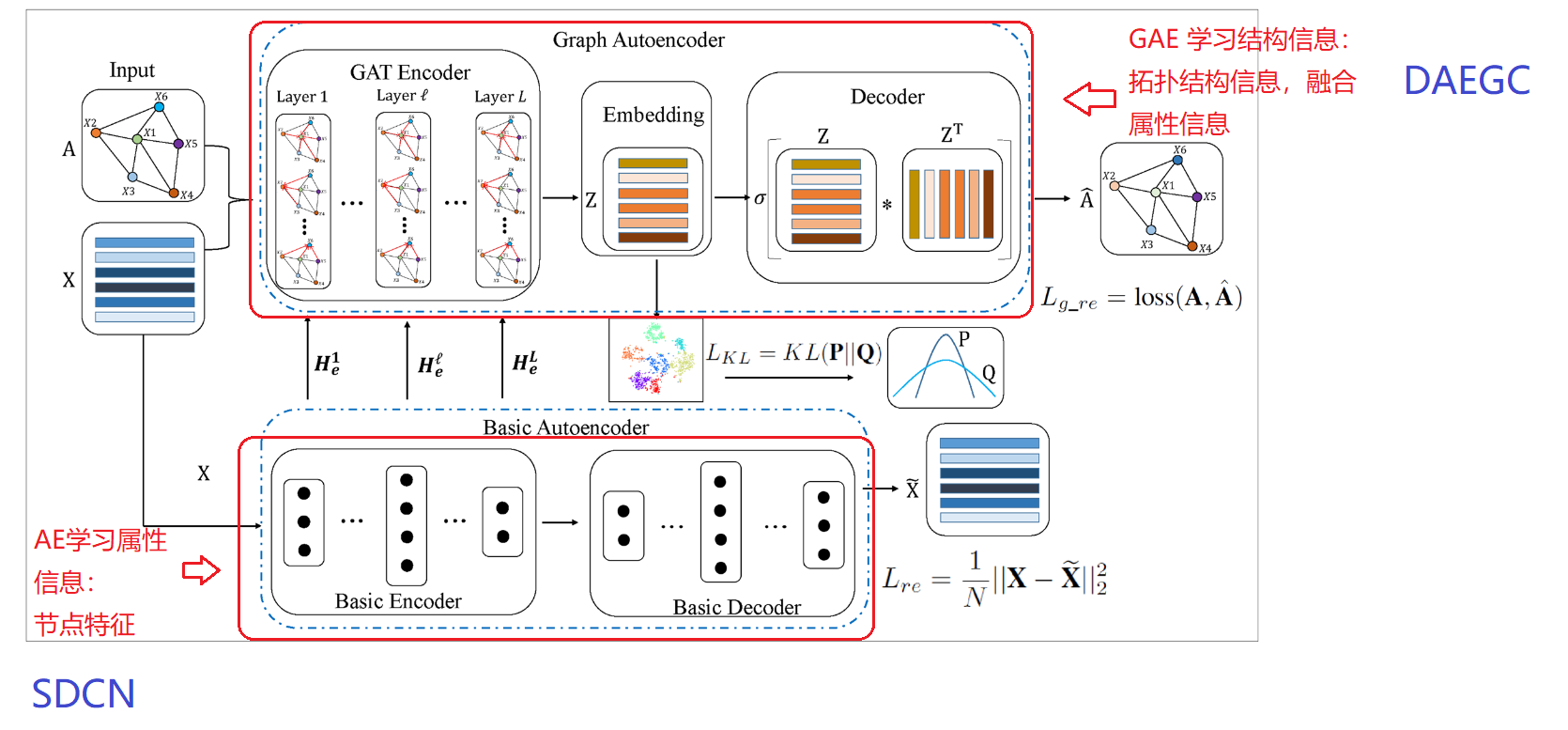
EFR-DGC模型架构 主要由3个模块组成： 学习节点属性信息的基本编码器AE 来自SCDN论文, 学习图的结构信息即拓扑结构信息，并融合属性信息的带有注意力机制的图编码器 来自DAEGC 论文，以及带有自监督的聚类模块**。

2.模型的模块详细介绍

1. AE编码器 学习属性信息

我们使用具有多个全连接层的基本自动编码器 (AE) 从原始特征数据X中学习分层属性信息，并将其学习到的信息嵌入到潜在空间中的紧凑特征表示中和SCDN中论文一模一样。

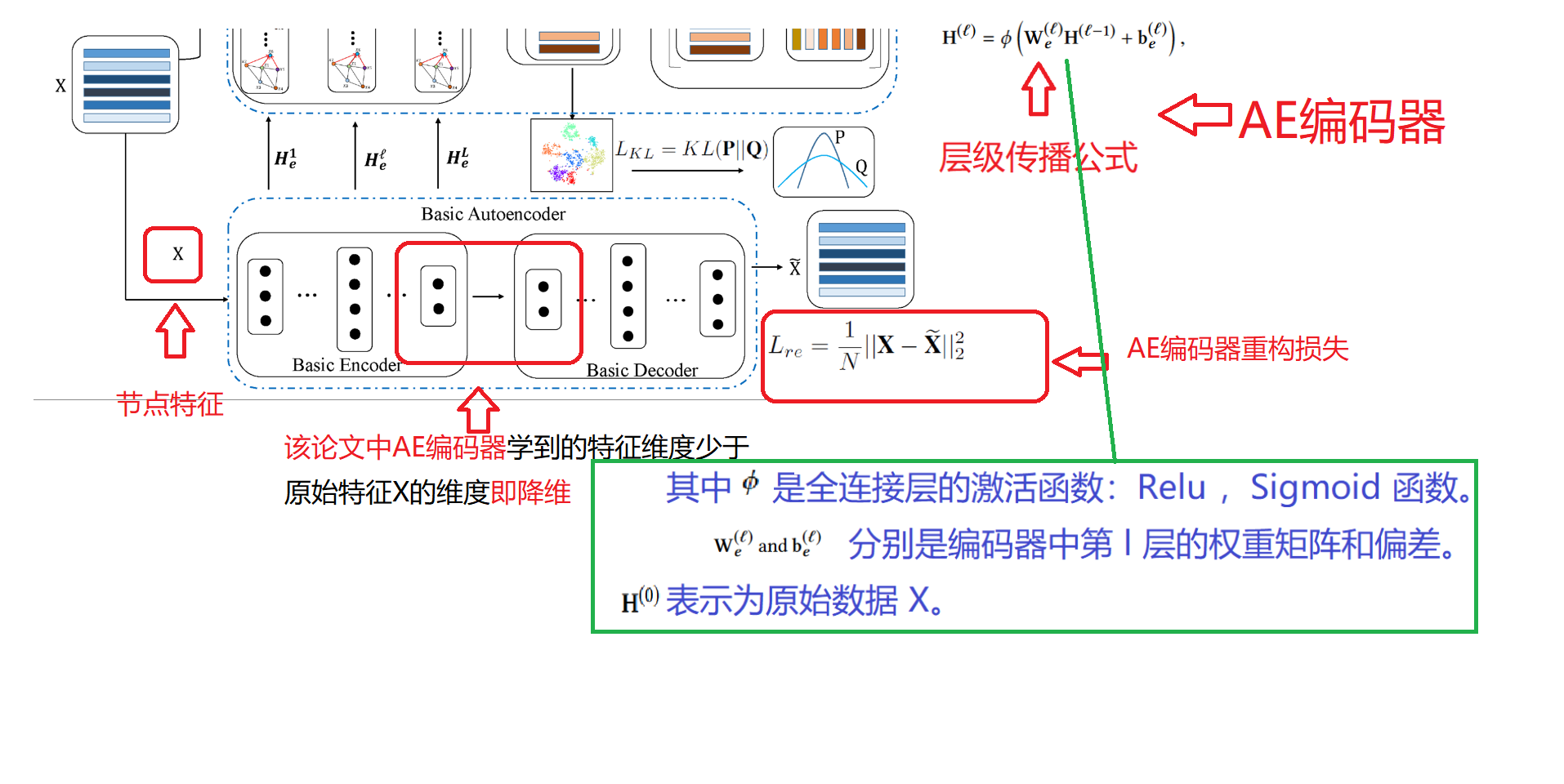
2.带有注意力机制的GAE

我们通过图注意力网络 (GAT) 构建图自动编码器 (GAE)，并将其与基本 AE 相结合以生成增强的特征表示。

1. 编码器encoding

　EFR-DGC 认为图具有复杂的结构关系，建议在编码器中利用高阶邻居。我们通过考虑图中的 t 阶邻居节点获得邻近矩阵M： t参数可以根据实验结果，自己调节，也即是输入参数`

接下来计算顶点之间的图注意力系数: 顶点间的图注意力是不对成的 即 aij 不等于aji

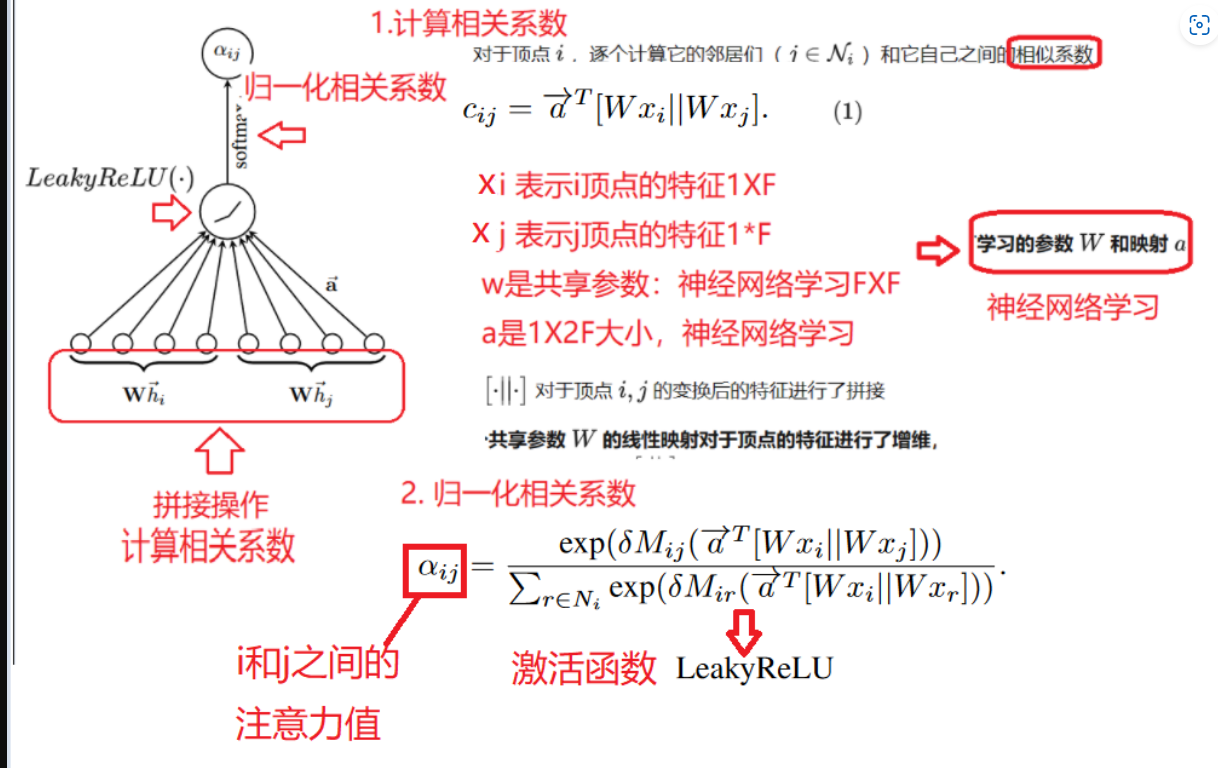
图注意层得到图注意力自动编码器的编码器部分层级更新:

2. 解码器decoding

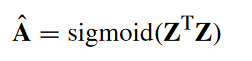
3. 损失函数计算

采用交叉熵损失函数：

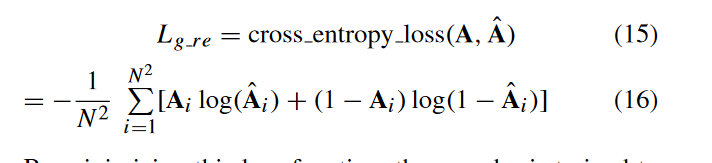
3. 自监督机制

我们使用学生 t 分布 作为函数来计算节点 i 的特征表示 zi 与聚类中心 uj 之间的相似度：聚类中心 u 是用基于 Z 的 K-means 初始化的。

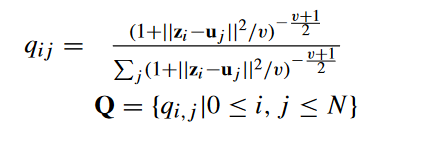
*qiu*表示节点i属于簇u的概率，将其看作是每个节点的软聚类分配标签，如果值越大，那么可信度越高 。通过平方运算将这种可信度放大，

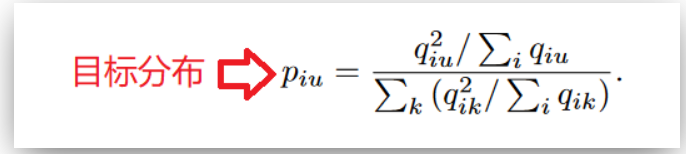
自训练聚类模块的损失函数采用KL 散度：

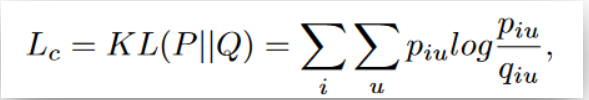
聚类损失然后迫使当前分布 Q 逼近目标分布 P ，从而将这些“置信分配”设置为软标签来监督 Q 的嵌入学习

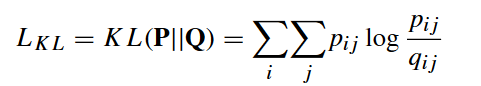
4. 总损失函数

🔤KL散度被视为聚类损失。整体学习目标由两部分组成，即基本AE和GAE的重构损失，以及聚类损失：🔤

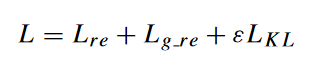
5. 算法流程图

3. 实验结果分析

1. 比较方法分析

K-means[48]是经典聚类算法的代表。

AE、DEC 和 IDEC 代表了深度学习方法，它们通过神经网络学习聚类任务的潜在数据表示。

GAE/VGAE、SDCN 和我们的基线方法 DAEGC 是通过图神经网络学习潜在数据表示的深度图聚类方法。

2. 模型好的原因

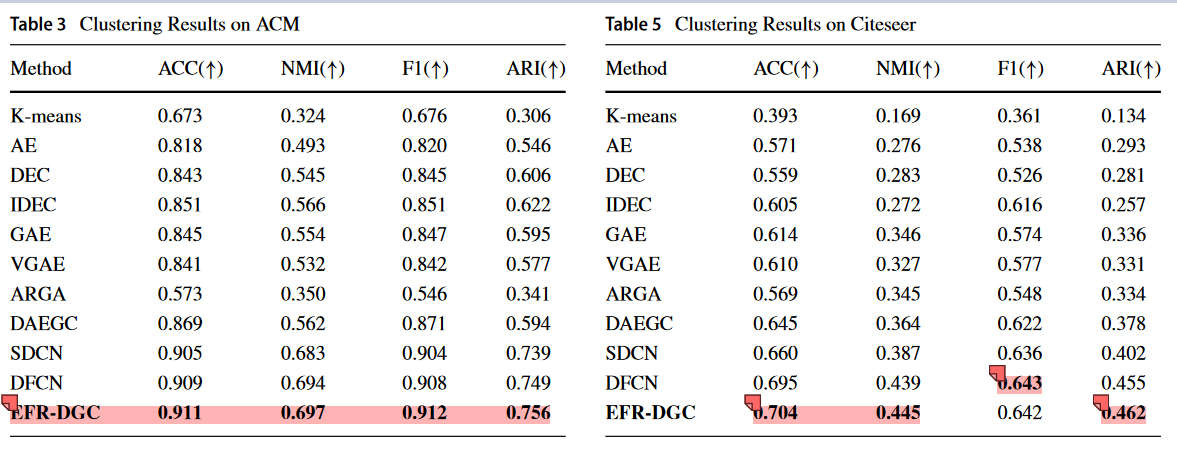
原因是我们的EFRDGC考虑了数据属性信息，为节点分区提供了重要依据。同时，自监督机制在指导模型优化方面也发挥着重要作用。结果，EFR-DGC生成消除了节点特征表示中的属性不足，以提高同一社区内的节点凝聚力并减少不同社区之间的重叠。

即 SDCN 模型中 AE 模块能有效提取 节点的属性信息。解决节点的属性不足能力。

即DAEGC 模型中带有GAT 的GAE ，能有效提取图的结构的信息。并有效融合节点的属性信息。

3. DBLP 和cora数据集实验分析

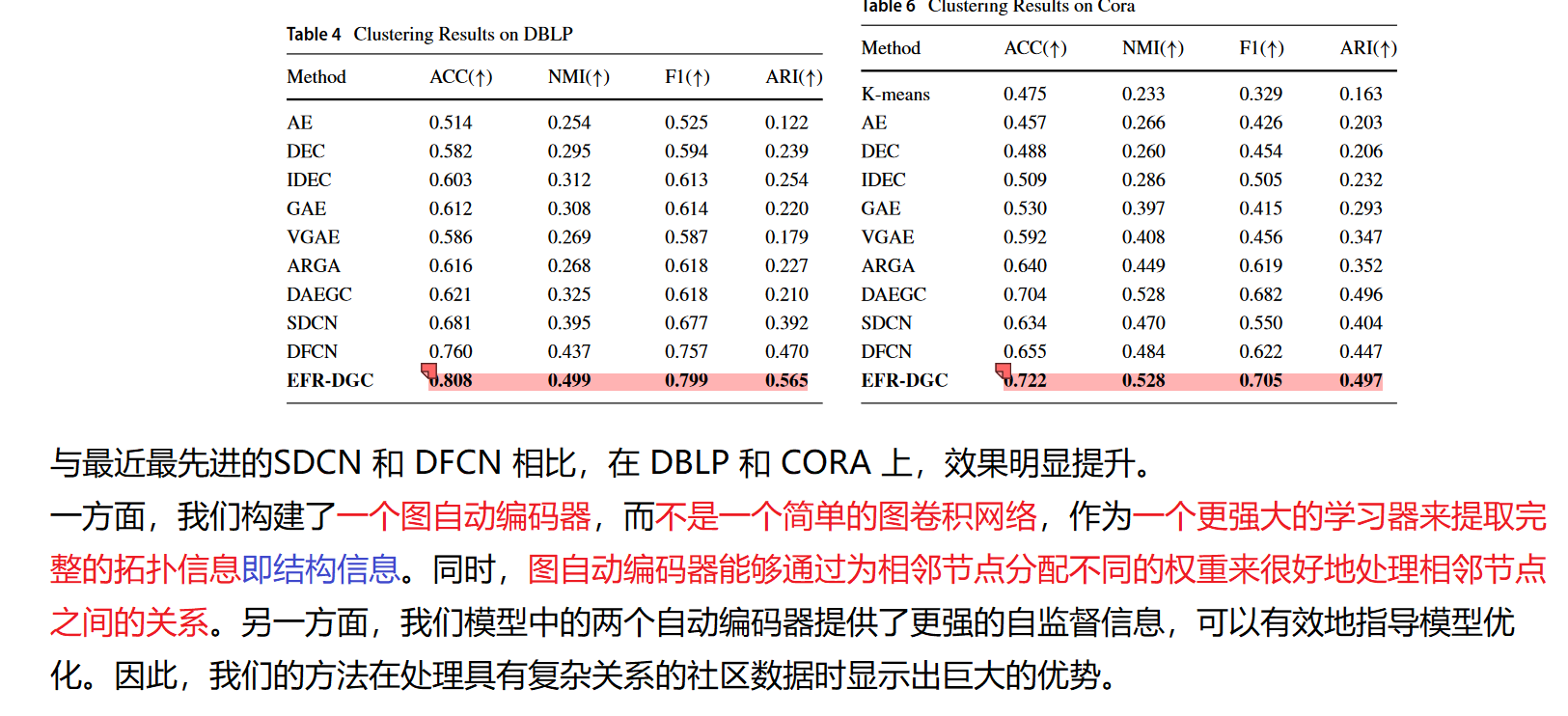
原因一：

DBLP 和 Cora 比 ACM 和 Citeseer 中的更密集。即 DBLP 和 Cora 的相邻矩阵更密集。节点之间更密集的连接通常意味着更复杂的关系。 EFR-DGC 模型中的图注意力网络具有更多在处理此类数据方面的优势，因为它可以学习不同邻域的权重更精确地表示居中节点的节点

原因二：

一方面，我们构建了一个图自动编码器，而不是一个简单的图卷积网络，作为一个更强大的学习器来提取完整的拓扑信息即结构信息。同时，图自动编码器能够通过为相邻节点分配不同的权重来很好地处理相邻节点之间的关系。另一方面，我们模型中的两个自动编码器提供了更强的自监督信息，可以有效地指导模型优化。因此，我们的方法在处理具有复杂关系的社区数据时显示出巨大的优势即 处理节点密集的图

4. 消融实验分析

1. EFR-DGC 的有效性

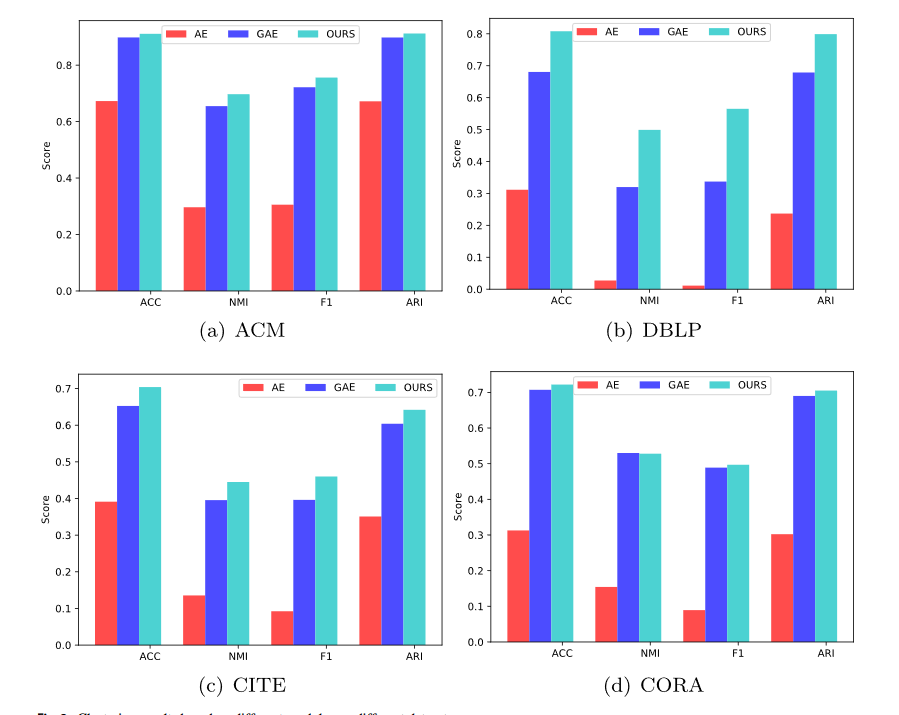
我们分别使用 AE、GAE 和 EFR-DGC 生成特征表示。然后，特征表示用于在四个数据集中进行聚类任务

实验分析：

单一的AE模型不擅长处理图数据，因为它没有考虑节点之间的关系： 即结构信息 没有考虑。

与GAE（DAEGC中使用的模型）相比，EFR-DGC中的模块层包含更充分和可区分的属性信息

结果表明来自基本 AE 的分层属性信息可以帮助 GAE 丰富数据表达。 多维和多粒度信息，从而提高特征表达能力

2. 超参数

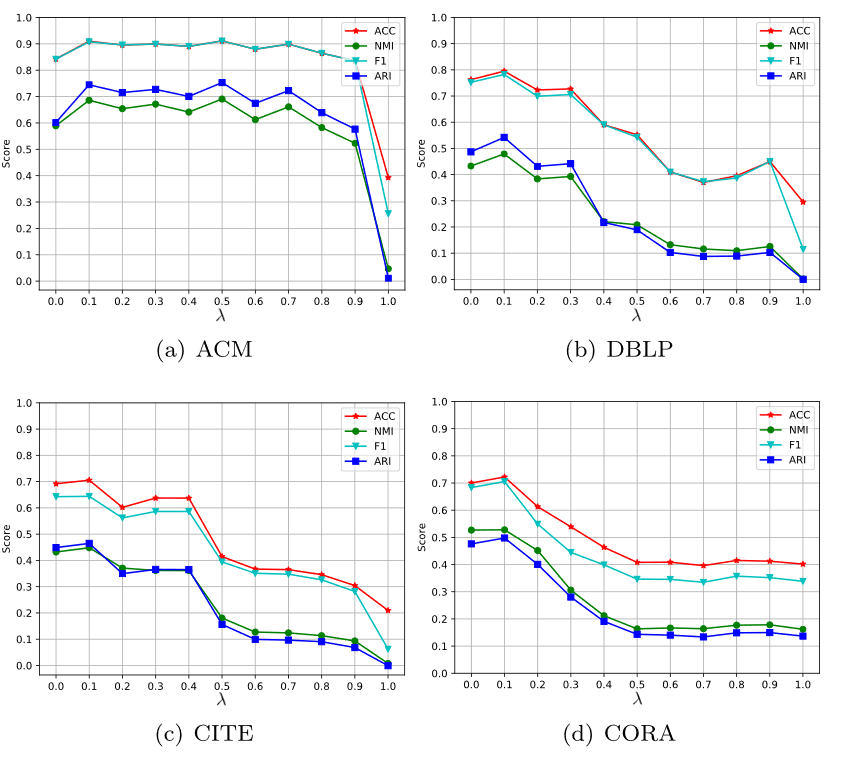
1. 超参数是 中的 λ平衡了两个部分（AE 和 GAE）对隐藏表示的影响

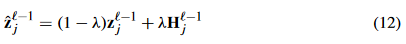
有两个重要的超参数决定了我们模型的性能。第一个超参数是 (12) 中的 λ，它平衡了两个部分（AE 和 GAE）对隐藏表示的影响。换句话说，λ 决定了 GAE 层中的新隐藏表示从 AE 模块接收了多少属性信息。我们对 λ 进行了网格搜索，正如我们所见，当 λ 设置为 0.1 时，我们的模型在所有数据集上都达到了最高的精度

2. 超参数 ε 控制聚类损失

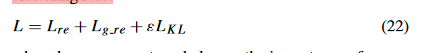
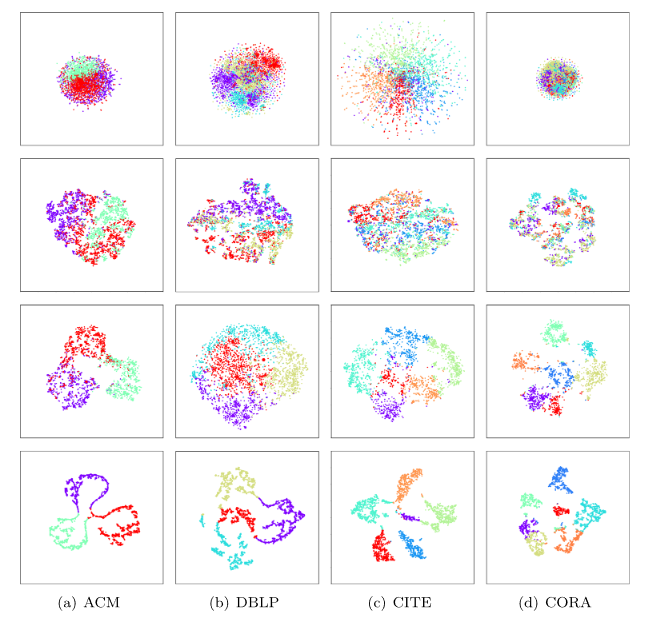
损失函数 (22) 中的第二个超参数 ε 控制聚类损失的影响。我们进行实验以显示超参数对所有数据集的影响。

图 5 说明了我们的模型在参数集 {0.01, 0.1, 1.0, 10, 100} 中的性能变化。实验结果表明，当 ε = 1.0 时，我们的模型达到最佳性能。同时，我们的模型是稳健的，因为它不会随着参数值的变化而发生剧烈变化

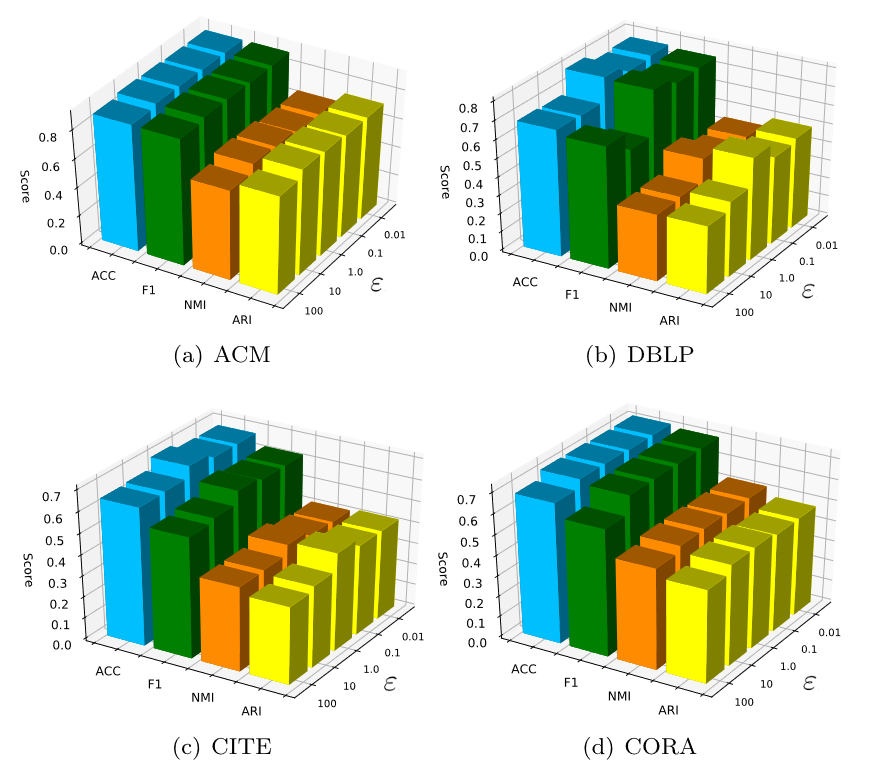
3. 可视化特征表示

如图 6 所示，**第一行对应于原始社区数据的分布，第二行对应于基本自动编码器的表示分布，最后一行对应于我们的 EFR-DGC 的表示分布。正如我们所见，单个 AE 或 GAE 生成的特征表示无法有效分离。相反，我们的方法可以减少不同社区的重叠，并使同一社区内的节点彼此封闭。特别是，与 GAE 模型（在我们的基线方法 DAEGC 中使用）相比，我们的模型增强了属性信息表示，从而提高了社区节点的可区分性。