HashMap中的位运算
二进制基础回顾
以下操作相对正整数的二进制而言,对非整数不太适用。
二进制转十进制
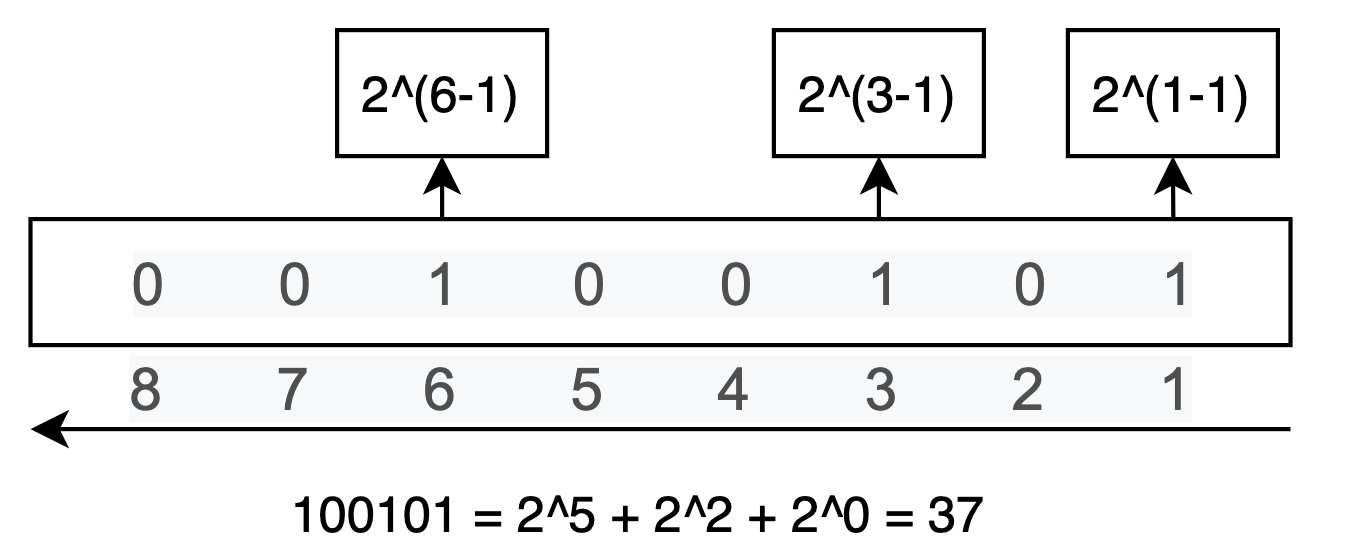
在二进制中,位权是2的幂,所以每一位所代表的权值从右到左分别为2^(1-1) 、2^(2-1) 、... 、 2^(n-1) ,第n位的权值为2的(n-1)次幂。
所以: 100101 = 2^5 + 2^2 + 2^0 = 37。
二进制位移操作
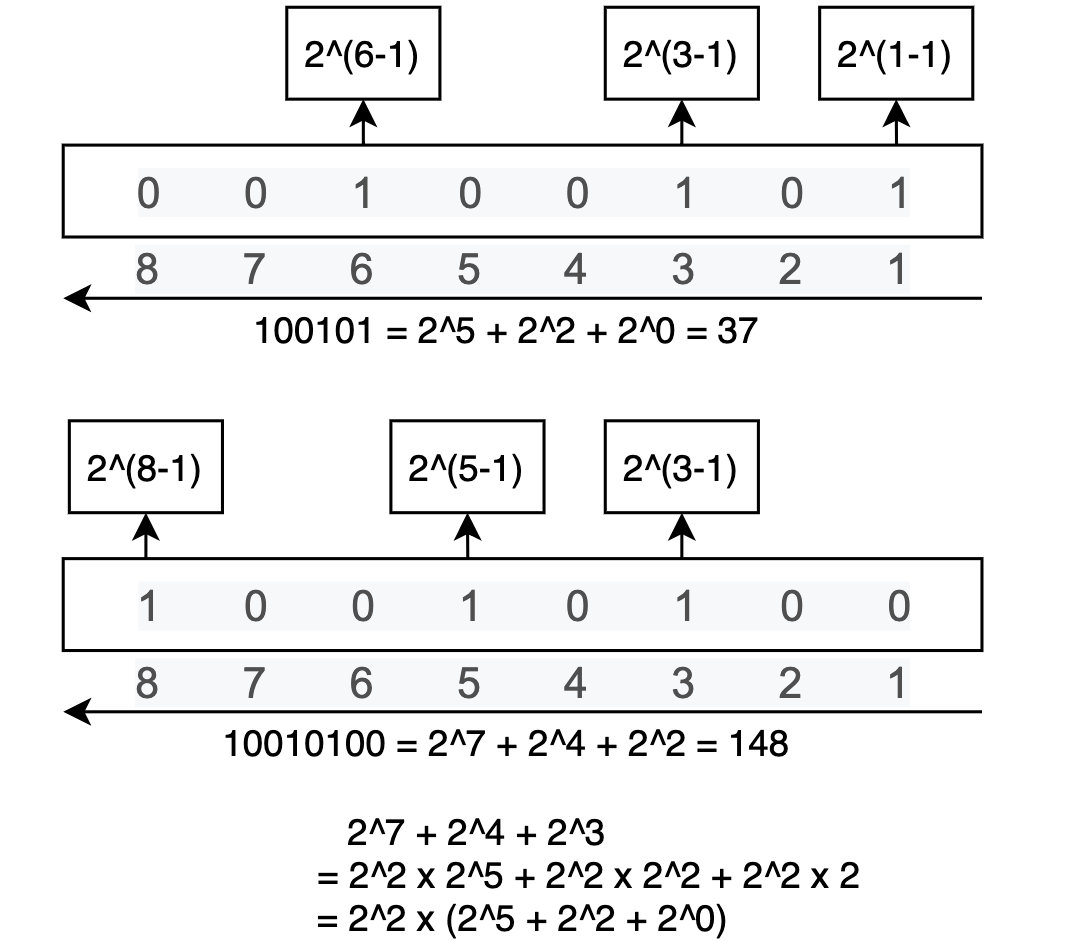
当一个二进制数左移一位,右补"0"的时候,这个数每一位的权值就变成了原来的两倍,那么整个数值也扩大了2倍;当这个数左移n位的时候,这个数就扩大到原来的2^n 倍。同样的,往右移动n位,左补"0",相当于除以2^n ,如果考虑到右边数位被舍弃的问题,这就相当于除以2^n 然后取整数。这和十进制是一样的,十进制数字左移n位,就是扩大到原来的10^n 倍……
“按位与”与取模
在HashMap和ThreadLocal源码中可以看到类似这样的操作:
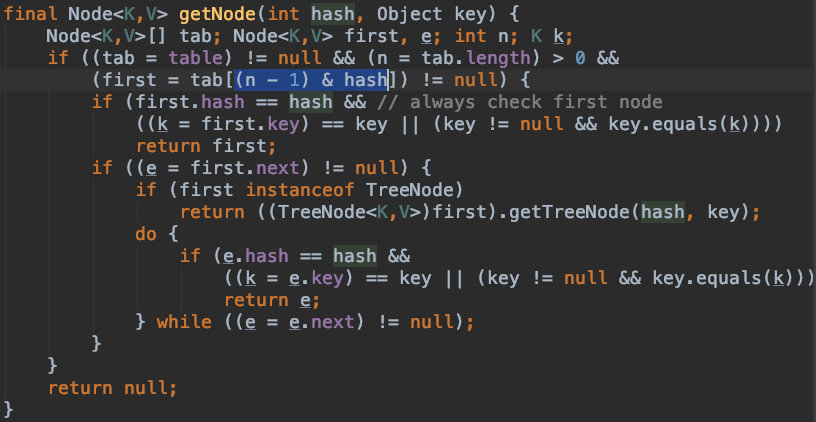
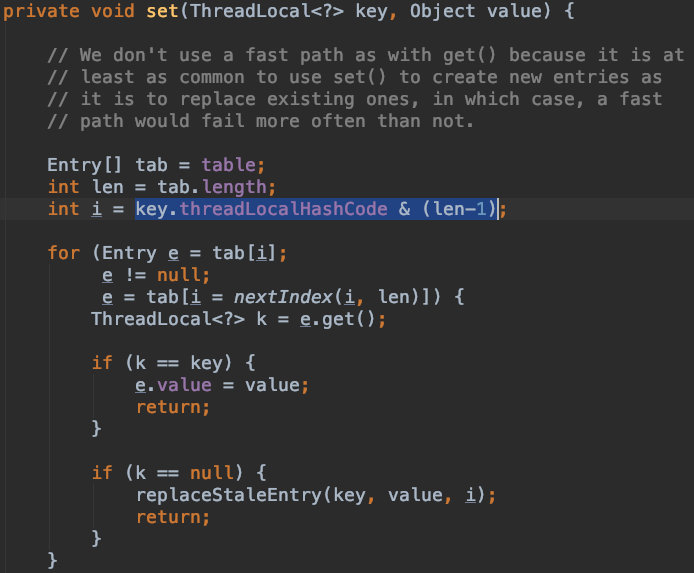
在这里,“按位与”操作的作用是取模,其中"n"和"len"都是数组的长度,此处代码是要把元素的hash值映射成数组的索引(下标),以此来决定该元素的存储位置。
由于hash值相对于数组的长度来说很大,所以不能把hash值直接一一映射为数组下标,而是对其取模,通过余数来映射。
比如一个元素的hash值为123456,而数组的长度为7,取模123456%7=4,那么可以把元素存到数组中下标为4的位置,获取该元素时,同样用hash值和数组长度取模,在数组中对应位置获取。这是“散列表”的相关知识。关于详细的取模的意义,详见百度-散列表。
原理
当n等于2的次幂时,"hash%n"和"hash&(n-1)"等价,求证如下:
设n=16,hash=2740216402

- 当n取2的幂时,n的二进制表示有个特点——除去左边补全的0外,数字以"1"开头,后面全是"0";n-1的二进制表示也有一个特点——n-1的二进制位数比n少一位,数位左边全是"0",右边全是"1"。

- n-1与hash值进行“按位与”操作时,就相当于把hash前面部分舍去,只保留后面部分(这与掩码
类似,在源码注释部分,也把这操作称为"mask")。这实际上就是取模操作,后面的保留部分棕红色的0010就是“余数”。为什么这部分是余数?接着往下求证:
把hash值2740216402的二进制表示拆成两部分,可变为:
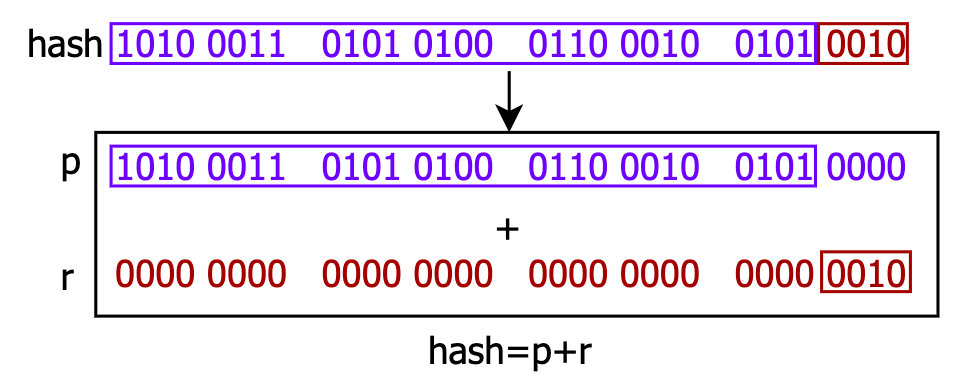
解析: r为保留部分,hash=p+r
p与n是存在倍数关系的,如下所示:

总结上述数量关系,可得:"hash = p + r = q * n + r",即hash = q * n + r,逆运算就是 hash ÷ n = q...r,当然,想要让逆运算的算式成立,前提条件是r要小于n,又因为r比n少一位,r自然比n小,所以该算式成立。因此当n等于2的幂,hash&(n-1)=hash%n。
简单的说,就是当n等于2的次幂时,n-1与hash进行“按位与”运算,n-1像掩码一样,恰好把hash中n的倍数舍去,只保留不足一倍n的余数部分。hash&(n-1)=hash%n

HashMap中的异或操作
在HashMap源码中有这样一段代码:
/**
* Computes key.hashCode() and spreads (XORs) higher bits of hash
* to lower. Because the table uses power-of-two masking, sets of
* hashes that vary only in bits above the current mask will
* always collide. (Among known examples are sets of Float keys
* holding consecutive whole numbers in small tables.) So we
* apply a transform that spreads the impact of higher bits
* downward. There is a tradeoff between speed, utility, and
* quality of bit-spreading. Because many common sets of hashes
* are already reasonably distributed (so don't benefit from
* spreading), and because we use trees to handle large sets of
* collisions in bins, we just XOR some shifted bits in the
* cheapest possible way to reduce systematic lossage, as well as
* to incorporate impact of the highest bits that would otherwise
* never be used in index calculations because of table bounds.
*/
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
先简单了解下java的位移操作:
- <<:左移运算符,num << 1,相当于num乘以2
- >>:右移运算符,num >> 1,相当于num除以2
- >>>:无符号右移,忽略符号位,空位都以0补齐
关于异或的知识:
- A ^ 0 = A,即当0与一个数(0/1)进行异或操作时,结果等于这个数本身,如0 ^ 0 = 0、 0 ^ 1 = 1;
- A ^ 1 = ! A,即当1与一个数(0/1)进行异或操作,结果等于非-此数,或者说取反,如1 ^ 0 = 1, 1 ^ 1 = 0;
再来画下图看这里代码干了些什么:

好了,图已经画出来了,接下来对该操作进行解读——代码先是这样……然后那样……最后又……
解读个鬼啊,其实这样很难看出这段操作的意义,所以还是看代码上面的注释吧,注释写得很清楚了,这段代码主要作用是利用hashcode的结果来生成更加“散列”的哈希值hash,什么意思?接着往下看:
接着上一小节的“按位与”讲起,思考下,如果用原始的"hashcode"执行上小节的“按位与操作”会有怎样的问题。

引用上面的旧图分析,如果直接用原始的hashcode来取模,然后映射为数组的下标,这样会产生一个很大的问题。通常数组的长度不会太大,即上图红棕色的部分不会很长,那么原始的hashcode的“高位”对最后的余数的影响会很小,意思就是,只要hashcode后面的四位数为"0010",不管前面蓝紫色部分是什么,“hashcode&(n-1)”的结果始终为"0010",映射为数组的下标就是“2”,这样会非常容易造成“哈希冲突”(又名“哈希碰撞”)。
所以需要采取一种策略,使得hashcode的每一位,都尽量参与运算,尽量对取模结果产生影响,充分利用hashcode的每一位,使得取模的结果更加“零散”。因此,HashMap的源码给出了以上的方法。
hashcode长度为32位,右移16位,就是给原始的hashcode“折成两半”,把高位的一半与低位的一半对齐,然后通过异或操作把高位和低位“结合”起来。
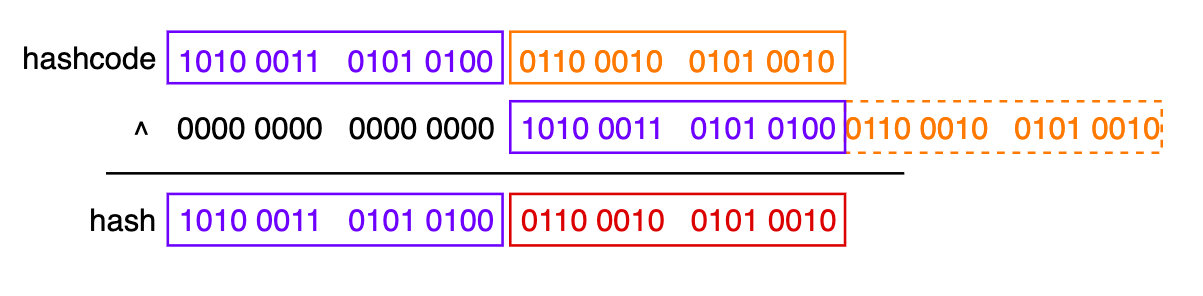
生成的新的hash值,其高位部分(左边16位蓝紫色部分)保留了原hashcode的高位,低位部分(红色部分)保留了原来的高位和低位的“特征”——如果原来高位部分某一位发生改变,则影响到结果的对应位;如果原来低位某一位发生改变,也同样影响到结果相应的位。
这里有一个问题,为什么要用异或操作?因为只能用异或操作,因为“与”和“或”不能很好的保留操作数的特征:
- 使用“与”操作时,当一个数为“0”,则结果必然为“0”,不必考虑另一个操作数;
- 使用“或”操作时,当一个操作数为“1”,则结果必然为“1”;
- 使用“异或”操作时,需要知道两个操作数才能决定结果。
当用上述方法生成新的hash值后,原来的hashcode的每一位都对最终的取模结果产生了影响,这时在一定程度上可以使得生成的余数更加均匀,更加“散列”,使得发生“碰撞”的几率降低。


