拉普拉斯变换
拉普拉斯变换是应用数学中常用的一种积分变换,又名拉氏转换,其符号为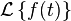 。拉氏变换是一个线性变换,可将一个有引数实数t(t ≥ 0)的函数转换为一个引数为复数s的函数:
。拉氏变换是一个线性变换,可将一个有引数实数t(t ≥ 0)的函数转换为一个引数为复数s的函数:
拉氏变换在大部份的应用中都是对射的,最常见的f(t)和F(s)组合常印制成表,方便查阅。拉普拉斯变换得名自皮埃尔-西蒙·拉普拉斯,他在机率论的研究中首先引入了拉氏变换。
拉氏变换和傅里叶变换有关,不过傅里叶变换将一个函数或是信号表示为许多弦波的叠加,而拉氏变换则是将一个函数表示为许多矩的叠加。拉氏变换常用来求解微分方程及积分方程。在物理及工程上常用来分析线性非时变系统,可用来分析电子电路、谐振子、光学仪器及机械设备。在这些分析中,拉氏变换可以作时域和频域之间的转换,在时域中输入和输出都是时间的函数,在频域中输入和输出则是复变角频率的函数,单位是弧度每秒。
对于一个简单的系统,拉氏变换提供另一种系统的描述方程,可以简化分析系统行为的时间[1]。像时域下的线性非时变系统,在频域下会转换为代数方程,在时域下的卷积会变成频域下的乘法。
目录
[隐藏]
正式定义[编辑]
对于所有实数t ≥ 0,函数f(t)的拉普拉斯变换是函数F(s),定义为:
参数s是一个复数:
![s = \sigma + i \omega, \,]() σ和ω为实数。
σ和ω为实数。
拉普拉斯变换的其他表示法中使用 或
或 而非F。
而非F。 是一个运算符号,它代表对其对象进行拉普拉斯积分
是一个运算符号,它代表对其对象进行拉普拉斯积分 ;
; 是
是 的拉普拉斯变换结果。
的拉普拉斯变换结果。
拉普拉斯逆变换[编辑]
拉普拉斯逆变换有许多不同的名称,如维奇积分、傅立叶-梅林积分、梅林逆公式,是一个复积分:
其中γ是一个使F(s)的积分路径在收敛域内的实数。
拉普拉斯变换的存在性[编辑]
关于一个函数 的拉普拉斯变换,只有在拉普拉斯积分是收敛的情况下才存在。也就是说,
的拉普拉斯变换,只有在拉普拉斯积分是收敛的情况下才存在。也就是说, 必须是在对于
必须是在对于 的每一个有限区间内都是间断性连续的,且当
的每一个有限区间内都是间断性连续的,且当 趋于无穷大的时候,
趋于无穷大的时候, 是指数阶地变化。
是指数阶地变化。
拉普拉斯变换的基本性质[编辑]
函数f(t)和g(t)的拉普拉斯变换分别为F(s)和G(s):
下面的表格是一系列单边拉普拉斯变换的性质:[2]
| 时域 | s域 | 注释 | |
|---|---|---|---|
| 线性叠加 |  |
 |
可以用积分的基本规则证明。 |
| 时域微分 | 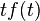 |
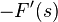 |
F′是F的一阶导数。 |
| 频域微分 | 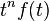 |
 |
更一般的形式是F(s)的n阶导数。 |
| 微分 |  |
 |
f是一个可微函数,并且其导数为指数类型。这条性质可以通过分部积分得到。 |
| 二阶微分 |  |
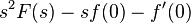 |
f为二阶可微且二阶导数是指数型的。通过对f′(t)应用微分性质可得。 |
| 一般微分 |  |
 |
f为n阶可微,其n阶导数是指数型的。通过数学归纳法证明。 |
| 频率积分 |  |
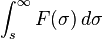 |
这是由频率微分和条件收敛推导出来的。 |
| 积分 |  |
 |
u(t)是阶跃函数,注意到 (u ∗ f)(t) 是u(t)和f(t)的卷积。 |
| 时间标度 | 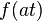 |
 |
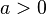 |
| 频率平移 | 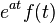 |
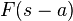 |
|
| 时域平移 |  |
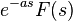 |
u(t)表示阶跃函数 |
| 乘法 |  |
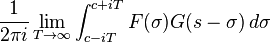 |
积分沿完全处在F收敛域内的竖直线Re(σ) = c。[3] |
| 卷积 |  |
 |
|
| 复共轭 |  |
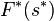 |
|
| 互相关 |  |
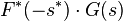 |
|
| 周期函数 |  |
 |
f(t)是一个周期为T的周期函数,于是对所有t ≥ 0,有'f(t) = f(t + T)。这条性质是时域平移和几何级数的结果。 |
- 初值定理:
![f(0^+)=\lim_{s\to \infty}{sF(s)}.]() ,要求
,要求![{F(s)}]() 为真分式,即分子的最高次小于分母的最高次,否则使用多项式除法将
为真分式,即分子的最高次小于分母的最高次,否则使用多项式除法将![{F(s)}]() 分解
分解
- 终值定理:
![f(\infty)=\lim_{s\to 0}{sF(s)}]() ,要求sF(s)的所有极点都在左半复平面或原点为单极点。
,要求sF(s)的所有极点都在左半复平面或原点为单极点。
变换简表[编辑]
原函数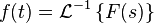 |
转换后函数 |
收敛区域 |
 |
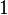 |
 |
 |
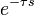 |
|
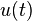 |
 |
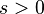 |
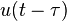 |
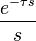 |
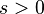 |
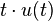 |
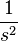 |
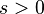 |
 |
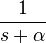 |
 |
 |
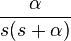 |
 |
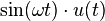 |
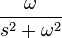 |
 |
 |
 |
 |
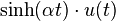 |
 |
 |
 |
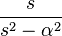 |
 |
 |
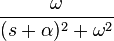 |
 |
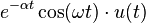 |
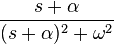 |
 |
 |
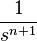 |
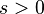 |
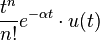 |
 |
 |
![\sqrt[n]{t} \cdot u(t)](http://upload.wikimedia.org/math/4/8/6/486b3056c275d0abfe2730f87a747f9f.png) |
 |
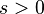 |
 |
![- { t_0 \over s} \ [ \ \ln(t_0 s)+\gamma \ ]](http://upload.wikimedia.org/math/6/e/8/6e8a76493bbae4b1d845742deeebdb01.png) |
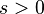 |
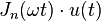 |
 |
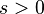  |
 |
 |
 |
 |
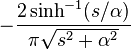 |
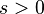 |
 |
||
 |
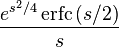 |
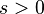 |
与其他变换的联系[编辑]
- 与傅里叶变换关系
令s = iω或s = 2πfi,有:
- 与z变换的联系
z 变换表达式为:
其中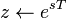 . 比较两者表达式有:
. 比较两者表达式有:

例子:如何应用此变换及其性质[编辑]
拉普拉斯变换在物理学和工程中是常用的;线性时不变系统的输出可以通过卷积单位脉冲响应与输入信号来计算,而在拉氏空间中执行此计算将卷积通过转换成乘法来计算。后者是更容易解决,由于它的代数形式。
拉普拉斯变换也可以用来解决微分方程,这被广泛应用于电气工程。拉普拉斯变换把线性差分方程化简为代数方程,这样就可以通过代数规则来解决。原来的微分方程可以通过施加逆拉普拉斯变换得到其解。英国电气工程师奥利弗·黑维塞第一次提出了一个类似的计划,虽然没有使用拉普拉斯变换;以及由此产生的演算被誉为黑维塞演算。
在工程学上的应用[编辑]
应用拉普拉斯变换解常变量齐次微分方程,可以将微分方程化为代数方程,使问题得以解决。在工程学上,拉普拉斯变换的重大意义在于:将一个信号从时域上,转换为复频域(s域)上来表示,对于分析系统特性,系统稳定有着重大意义;在线性系统,控制自动化上都有广泛的应用

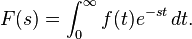

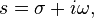 σ和ω为实数。
σ和ω为实数。

 ,要求
,要求 为真分式,即分子的最高次小于分母的最高次,否则使用
为真分式,即分子的最高次小于分母的最高次,否则使用 ,要求sF(s)的所有极点都在左半
,要求sF(s)的所有极点都在左半![\begin{align}
\hat{f}(\omega) & = \mathcal{F}\left\{f(t)\right\} \\[1em]
& = \mathcal{L}\left\{f(t)\right\}|_{s = i\omega} = F(s)|_{s = i \omega}\\[1em]
& = \int_{-\infty}^{\infty} e^{-\imath \omega t} f(t)\,\mathrm{d}t.\\
\end{align}](http://upload.wikimedia.org/math/a/6/4/a64f2756d3bfdca47f2130fb7c4ef72f.png)
![X(z) = \sum_{n=0}^{\infty} x[n] z^{-n}](http://upload.wikimedia.org/math/9/3/7/93762261ebf70b67ba079c79607646fa.png)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号