线性代数2

实数的集合表示法 (the notation for real numbers)

 实数: 所有非复数的数，也就是除了复数之外的所有数，例如: π ，-π ， e ， √2 ， 3 ， -3

所有实数集合的符号\R

Rn   实数中有序集的集合

R2   实数所有序列的集合

 

 

“多维的”实数 multiple dimensions of real numbers

“多维的”实数 multiple dimensions of real numbers

 

 

数字类型划分

数分为：实数和虚数
实数分为：有理数和无理数
有理数分为：整数和分数
整数分为：正整数,负整数和零
其中正整数和零又叫自然数

自然数 natural numbers　　0,1,2,3...

整数 integers　　...,-3,-2,-1,0,1,2,3...

有理数 rational numbers : m/n　　n不等于0

无理数 Irrational numbers :无限不循环小数　　√2,  π(3.14...) , e(2.71...)

实数 real numbers　　有理数和无理数的集合

虚数 imaginary numbers   虚数单位(imaginary unit)是i　　i2 = -1

 

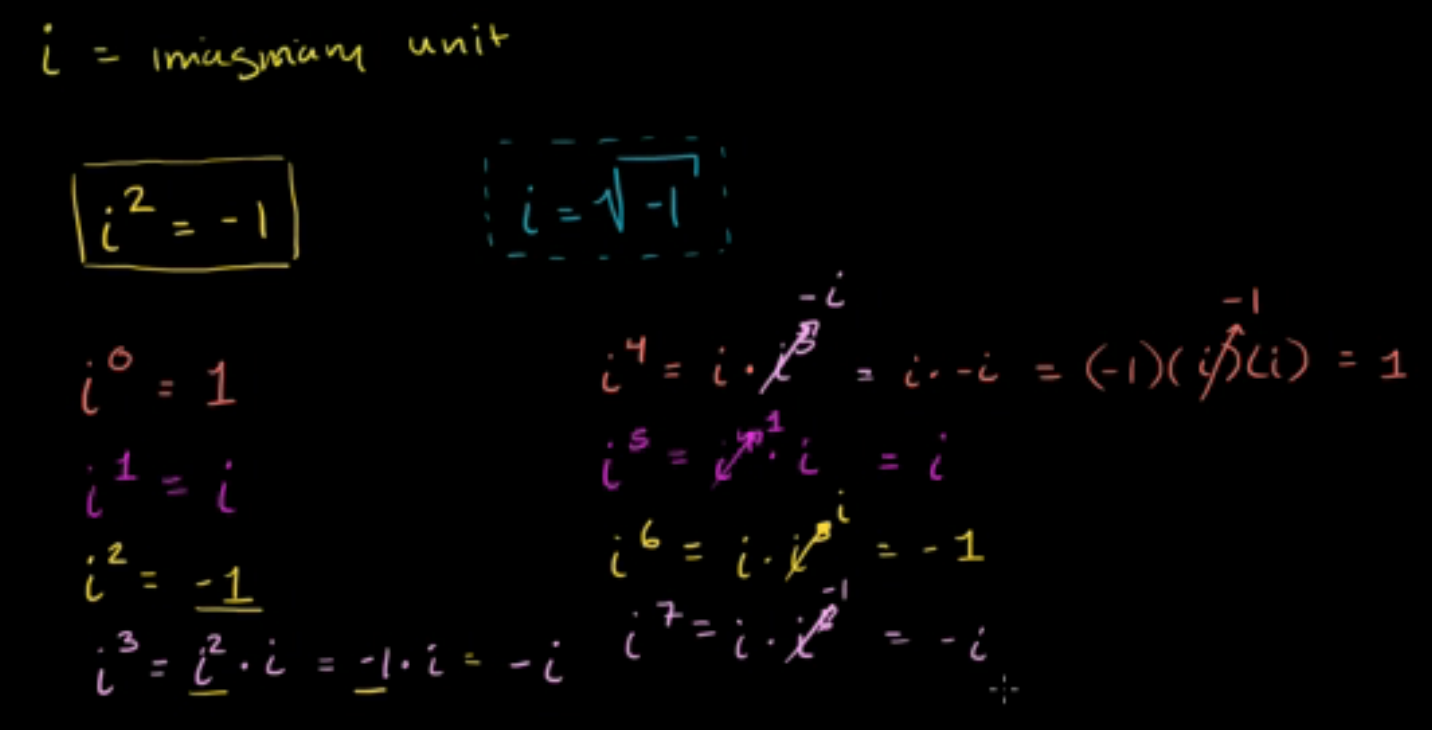
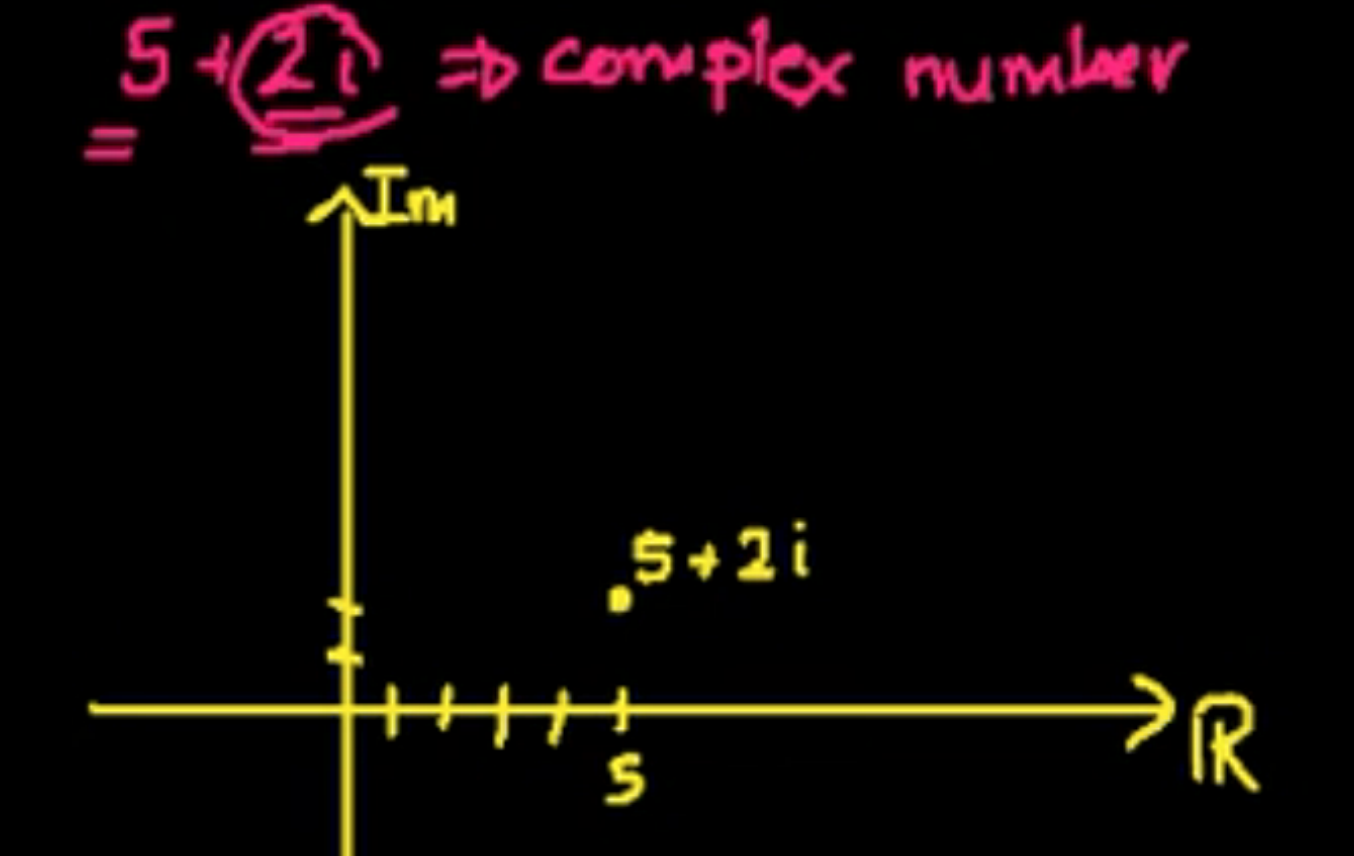
复数 complex numbers　　实数和虚数的组合　　a + bi　　a为实部，b为虚部

　　21的复数形式　　21 ＋ 0i

　　8i的复数形式　　0 ＋ 8i

 

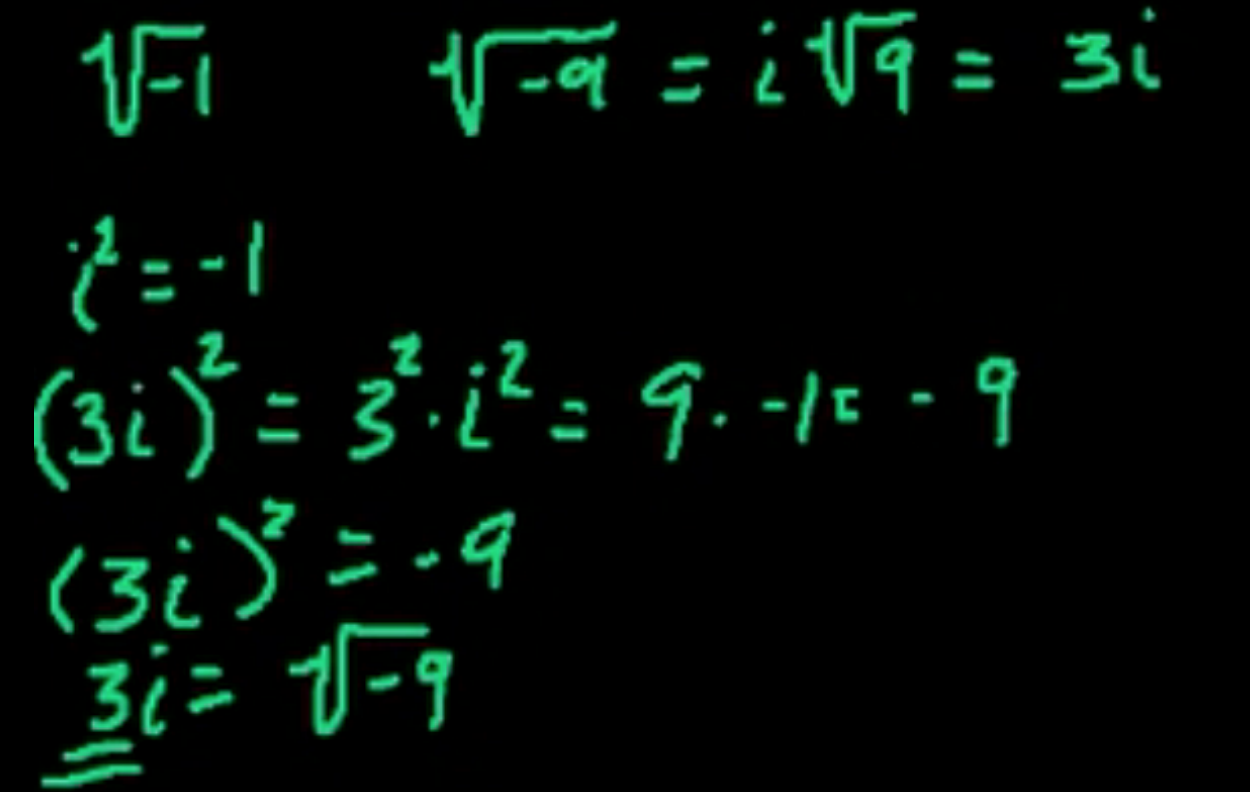
 共轭 conjugate　　共轭就是改变了虚轴上方向的对应复数，比如 a + bi = ， 共轭的符号是顶上一横 , a+bi和a-bi互为共轭

 

 

 

 

 

 

有理数

数学上，可以表达为两个整数比的数(a/b, b≠0)被定义为有理数，例如3/8，0.75(可被表达为3/4),与此对应的是无理数，如{\displaystyle {\sqrt {2}}}{\sqrt {2}}无法用整数比表示。
有理数与分数的区别，分数是一种表示比值的记法，如 分数{\displaystyle {\sqrt {2}}}{\sqrt {2}}/2 是无理数。
所有有理数的集合表示为Q，Q+,或{\displaystyle \mathbb {Q} }\mathbb{Q}。定义如下：

{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}:m\in \mathbb {Z} ,n\in \mathbb {Z} ,n\neq 0\right\}}\mathbb{Q} = \left\{\frac{m}{n} : m \in \mathbb{Z}, n \in \mathbb{Z}, n \ne 0 \right\}

有理数的小数部分有限或为循环。不是有理数的实数遂称为无理数。

维基百科：https://zh.wikipedia.org/wiki/%E6%9C%89%E7%90%86%E6%95%B0

 

无理数

无理数是指除有理数以外的实数，当中的“理”字来自于拉丁语的rationalis，意思是“理解”，实际是拉丁文对于logos“说明”的翻译，是指无法用两个整数的比来说明一个无理数。

非有理数之实数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环，即无限不循环小数。常见的无理数有大部分的平方根、π和e（其中后两者同时为超越数）等。无理数的另一特征是无限的连分数表达式。

维基百科：https://zh.wikipedia.org/wiki/%E7%84%A1%E7%90%86%E6%95%B8

 

实数

实数，是有理数和无理数的总称，前者如{\displaystyle 0}{\displaystyle 0}、{\displaystyle -4}{\displaystyle -4}、{\displaystyle 81/7}{\displaystyle 81/7}；后者如{\displaystyle {\sqrt {2}}}{\sqrt {2}}、{\displaystyle \pi }\pi 等。实数可以直观地看作小数（有限或无限的），它们能把数轴“填满”。但仅仅以枚举的方式不能描述实数的全体。实数和虚数共同构成复数。

所有实数的集合则可称为实数系（real number system）或实数连续统。任何一个完备的阿基米德有序域均可称为实数系。在保序同构意义下它是惟一的，常用{\displaystyle \mathbb {R} }\R表示。由于{\displaystyle \mathbb {R} }\R是定义了算数运算的运算系统，故有实数系这个名称。

实数可以分为有理数（如{\displaystyle 42}42、{\displaystyle -23/129}{\displaystyle -23/129}）和无理数（如{\displaystyle \pi }\pi 、{\displaystyle {\sqrt {2}}}{\sqrt {2}}），或者代数数和超越数（有理数都是代数数）两类。实数集合通常用字母{\displaystyle R}R或{\displaystyle \mathbb {R} }\R表示。而{\displaystyle \mathbb {R} ^{n}}\R^n表示{\displaystyle n}n维实数空间。实数是不可数的。实数是实分析的核心研究对象。

维基百科：https://zh.wikipedia.org/wiki/%E5%AE%9E%E6%95%B0

 

虚数

虚数，即实数部分为0的复数。“虚数”这个名词是17世纪著名数学家笛卡尔创制，因为当时的观念认为在真实世界中这是虚构或毫无用处的数字。后来在欧拉和高斯的研究之后，后来发现虚数可对应平面上的纵轴，与对应平面上横轴的实数同样真实。虚数轴和实数轴构成的平面称复数平面，复平面上每一点对应着一个复数。

每一个虚数可表达为bi，其中b是实系数，虚数bi的平方是−b2。例如，5i是一个虚数，其平方为−25。0被认为既是实数也是虚数。虚数单位{\displaystyle i\,}i\, 的定义是：

{\displaystyle i^{2}=-1\,}i^{2}=-1\,

或者

{\displaystyle i=+{\sqrt {-1}}\,}i=+{\sqrt {-1}}\,

{\displaystyle i}i 称为虚数单位。

生动形象解释虚数的意义：http://www.ruanyifeng.com/blog/2012/09/imaginary_number.html

维基百科：https://zh.wikipedia.org/wiki/%E8%99%9A%E6%95%B0

 

复数

复数，为实数的延伸，它使任一多项式方程式都有根。复数当中有个“虚数单位”{\displaystyle i}i，它是{\displaystyle -1}-1的一个平方根，即{\displaystyle i^{2}=-1}i ^2 = -1。任一复数都可表达为{\displaystyle x+yi}x + yi，其中{\displaystyle x}x及{\displaystyle y}y皆为实数，分别称为复数之“实部”和“虚部”。

复数的发现源于三次方程的根的表达式。数学上，“复”字表明所讨论的数域为复数，如复矩阵、复变函数等。

符号表示[编辑]

尽管可以使用其他表示法，复数通常写为如下形式

{\displaystyle a+bi}a+bi，

这里的a和b是实数，而i是虚数单位，它有着性质i ² = −1。实数a叫做复数的实部，而实数b叫做复数的虚部。实数可以被认为是虚部为零的复数；就是说实数a等价于复数a+0i。实部为零且虚部不为零的复数也被称作“纯虚数”；而实部为不为零且虚部也不为零的复数也被称作“非纯虚数”或“杂虚数”。

例如，3 + 2i是复数，它的实部为3虚部为2。如果z = a + ib，则实部（a）被指示为Re(z)或{\displaystyle \Re (z)}\Re (z)，而虚部（b）被指示为Im(z)或{\displaystyle \Im (z)}\Im (z)。

符号表示[编辑]

尽管可以使用其他表示法，复数通常写为如下形式

{\displaystyle a+bi}a+bi，

这里的a和b是实数，而i是虚数单位，它有着性质i ² = −1。实数a叫做复数的实部，而实数b叫做复数的虚部。实数可以被认为是虚部为零的复数；就是说实数a等价于复数a+0i。实部为零且虚部不为零的复数也被称作“纯虚数”；而实部为不为零且虚部也不为零的复数也被称作“非纯虚数”或“杂虚数”。

例如，3 + 2i是复数，它的实部为3虚部为2。如果z = a + ib，则实部（a）被指示为Re(z)或{\displaystyle \Re (z)}\Re (z)，而虚部（b）被指示为Im(z)或{\displaystyle \Im (z)}\Im (z)。

在某些领域（特别是电子工程，这里的i是电流的符号）中，虚部i被替代写为j，所以复数有时写为a + jb[1]。

所有复数的集合通常指示为C，或者用黑板粗体写为{\displaystyle \mathbb {C} }\mathbb {C} 。实数R可以被当作C的子集，通过把实数的所有成员当作复数: a = a + 0i。

等量关系[编辑]

复数中的虚数是无法比较大小的，即两个虚数只有相等和不等两种等量关系。

两个复数是相等的，当且仅当它们的实部是相等的并且它们的虚部是相等的。就是说，设a,b,c,d为实数,则a + bi= c + di当且仅当a = c并且b = d。

运算[编辑]

通过形式上应用代数的结合律、交换律和分配律，再加上等式i ² = −1，定义复数的加法、减法、乘法和除法:

  • 加法：{\displaystyle \,(a+bi)+(c+di)=(a+c)+(b+d)i}\,(a+bi)+(c+di)=(a+c)+(b+d)i
  • 减法：{\displaystyle \,(a+bi)-(c+di)=(a-c)+(b-d)i}\,(a+bi)-(c+di)=(a-c)+(b-d)i
  • 乘法：{\displaystyle \,(a+bi)(c+di)=ac+bci+adi+bdi^{2}=(ac-bd)+(bc+ad)i}\,(a+bi)(c+di)=ac+bci+adi+bdi^{2}=(ac-bd)+(bc+ad)i
  • 除法：{\displaystyle \,{\frac {(a+bi)}{(c+di)}}={\frac {(a+bi)(c-di)}{(c+di)(c-di)}}={\frac {ac+bci-adi-bdi^{2}}{c^{2}-(di)^{2}}}={\frac {(ac+bd)+(bc-ad)i}{c^{2}+d^{2}}}=\left({ac+bd \over c^{2}+d^{2}}\right)+\left({bc-ad \over c^{2}+d^{2}}\right)i}\,{\frac {(a+bi)}{(c+di)}}={\frac {(a+bi)(c-di)}{(c+di)(c-di)}}={\frac {ac+bci-adi-bdi^{2}}{c^{2}-(di)^{2}}}={\frac {(ac+bd)+(bc-ad)i}{c^{2}+d^{2}}}=\left({ac+bd \over c^{2}+d^{2}}\right)+\left({bc-ad \over c^{2}+d^{2}}\right)i

复数域[编辑]

复数可定义为实数{\displaystyle a,b}a, b组成的有序对，而其相关之和及积为：

  • {\displaystyle (a,b)+(c,d)=(a+c,b+d)}(a,b)+(c,d)=(a+c,b+d)，
  • {\displaystyle (a,b)\cdot (c,d)=(ac-bd,bc+ad)}(a,b)\cdot (c,d)=(ac-bd,bc+ad)，

复数数系是一个域，复数域常以{\displaystyle \mathbb {C} }\mathbb {C} 来表示。

一个实数{\displaystyle a}a等同于复数{\displaystyle (a,0)}(a,0)，故实数域为复数域的子域。虚数单位{\displaystyle i}i就是复数{\displaystyle (0,1)}(0,1)。此外，还有:

  • 加法单位元（“零元”）: {\displaystyle (0,0)}(0,0)
  • 乘法单位元（“幺元”）: {\displaystyle (1,0)}(1,0)
  • (a,b)的加法逆元: (−a, −b)
  • 非零 (a, b)的乘法逆元（倒数）: {\displaystyle \left({a \over a^{2}+b^{2}},{-b \over a^{2}+b^{2}}\right)}\left({a \over a^{2}+b^{2}},{-b \over a^{2}+b^{2}}\right)。

复数域亦可定为代数数的拓扑闭包或实数域的代数闭包。

复平面[编辑]

主条目：复平面

先把坐标轴画出来，横的叫实轴，竖的叫虚轴，然后确定0的位置，z=a十bi可以用二维空间来表示出来。
复数z可以被看作在被称为阿甘得图（得名于让-罗贝尔·阿冈，也叫做高斯平面）的二维笛卡尔坐标系内的一个点或位置向量。这个点也就是这个复数z可以用笛卡尔（直角）坐标指定。复数的笛卡尔坐标是实部 x = Re(z)和虚部y = Im(z)。复数的笛卡尔坐标表示叫做复数的“笛卡尔形式”、“直角形式”或“代数形式”。

维基百科：https://zh.wikipedia.org/wiki/%E5%A4%8D%E6%95%B0_(%E6%95%B0%E5%AD%A6)

 

posted @ 2018-01-04 14:36  大石头Oo  阅读(728)  评论(0)  编辑  收藏  举报