bzoj 1013 [JSOI2008]球形空间产生器sphere（高斯消元）

 

1013: [JSOI2008]球形空间产生器sphere

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 3584  Solved: 1863
[Submit][Status][Discuss]

Description

有一个球形空间产生器能够在n维空间中产生一个坚硬的球体。现在，你被困在了这个n维球体中，你只知道球面上n+1个点的坐标，你需要以最快的速度确定这个n维球体的球心坐标，以便于摧毁这个球形空间产生器。

Input

第一行是一个整数，n。接下来的n+1行，每行有n个实数，表示球面上一点的n维坐标。每一个实数精确到小数点后6位，且其绝对值都不超过20000。

Output

有且只有一行，依次给出球心的n维坐标（n个实数），两个实数之间用一个空格隔开。每个实数精确到小数点后3位。数据保证有解。你的答案必须和标准输出一模一样才能够得分。

Sample Input

2
0.0 0.0
-1.0 1.0
1.0 0.0

Sample Output

0.500 1.500

HINT

数据规模：

对于40%的数据，1<=n<=3

对于100%的数据，1<=n<=10

提示：给出两个定义：

1、 球心：到球面上任意一点距离都相等的点。

2、 距离：设两个n为空间上的点A, B的坐标为(a1, a2, …, an), (b1, b2, …, bn)，则AB的距离定义为：dist = sqrt( (a1-b1)^2 + (a2-b2)^2 + … + (an-bn)^2 )

Source

 

 

【思路】

       高斯消元

       列方程：设两点坐标为a[]，b[]，且x[]为球心坐标。则满足：

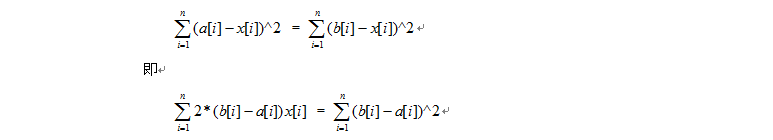
       每两个相邻点满足该式即可保证x为球心，所以只需要解n个方程。

       然后高斯消元解方程即可。

 

【代码】

 

#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;

typedef double dl;
const int N = 20;

dl A[N][N],a[N][N];
int n;

void gause() {
    int i,j,k,r;
    for(i=0;i<n;i++) {                        //消元 
        r=i;
        for(j=i+1;j<n;j++)
            if(fabs(A[j][i])>fabs(A[r][i])) r=j;
        if(r!=i) for(j=0;j<=n;j++) swap(A[r][j],A[i][j]);
        for(j=n;j>=i;j--)                   //使A[k][i]为0 
            for(k=i+1;k<n;k++)
                A[k][j]-=A[k][i]/A[i][i]*A[i][j];
    }
    for(i=n-1;i>=0;i--) {                    //回代 
        for(j=i+1;j<n;j++)
            A[i][n]-=A[j][n]*A[i][j];
        A[i][n]/=A[i][i];
    }
}

int main() {
    scanf("%d",&n);
    for(int i=0;i<=n;i++) for(int j=0;j<n;j++)
        scanf("%lf",&a[i][j]);
    for(int i=0;i<n;i++) {                    //构造方程组 
        for(int j=0;j<n;j++) A[i][j]=2*(a[i+1][j]-a[i][j]);
        for(int j=0;j<n;j++) A[i][n]+=a[i+1][j]*a[i+1][j]-a[i][j]*a[i][j];
    }
    gause();
    printf("%.3lf",A[0][n]); 
    for(int i=1;i<n;i++) printf(" %.3lf",A[i][n]);
    return 0;
}