bzoj1227 [SDOI2009]虔诚的墓主人(组合公式+离散化+线段树)

1227: [SDOI2009]虔诚的墓主人

Time Limit: 5 Sec  Memory Limit: 259 MB
Submit: 803  Solved: 372
[Submit][Status][Discuss]

Description

小W 是一片新造公墓的管理人。公墓可以看成一块N×M 的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好k 棵常青树。小W 希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少

Input

第一行包含两个用空格分隔的正整数N 和M，表示公墓的宽和长，因此这个矩形公墓共有(N+1) ×(M+1)个格点，左下角的坐标为(0, 0)，右上角的坐标为(N, M)。第二行包含一个正整数W，表示公墓中常青树的个数。第三行起共W 行，每行包含两个用空格分隔的非负整数xi和yi，表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。最后一行包含一个正整数k，意义如题目所示。

Output

包含一个非负整数，表示这片公墓中所有墓地的虔诚度总和。为了方便起见，答案对2,147,483,648 取模。

Sample Input

5 6
13
0 2
0 3
1 2
1 3
2 0
2 1
2 4
2 5
2 6
3 2
3 3
4 3
5 2
2

Sample Output

6

HINT

 

图中，以墓地(2, 2)和(2, 3)为中心的十字架各有3个，即它们的虔诚度均为3。其他墓地的虔诚度为0。 对于30%的数据，满足1 ≤ N, M ≤ 1,000。对于60%的数据，满足1 ≤ N, M ≤ 1,000,000。对于100%的数据，满足1 ≤ N, M ≤ 1,000,000,000，0 ≤ xi ≤ N，0 ≤ yi ≤ M，1 ≤ W ≤ 100,000， 1 ≤ k ≤ 10。存在50%的数据，满足1 ≤ k ≤ 2。存在25%的数据，满足1 ≤ W ≤ 10000。

 

 

【思路】

        组合公式+离散化+区间查询&单点修改。

　　　如果设每一个空格左右上下各有的树之数目为left[][],right[][],up[][],down[][]，则答案为

　　　　

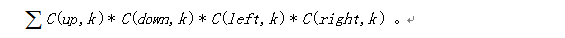
　　　考虑到nm很大，这里我们先进行离散化，离散化之后时间复杂度为O(ww)。

        考虑y同的两棵相邻的树（中间为空格）且x分别为ab，我们统计夹在中间的空格的分数，则为

　　　　　　

        前两项相同，因此只需要统计ab区间内的C之积即可，可以用线段树在O(logn)的时间内完成。

        具体操作：

　　　　依次扫描每一棵树：

         　　如果与前一棵树同y则累计答案。

         　　维护cy表示当前y扫描过的树之数目。

         　　   维护cx[]表示x被扫描过的树之数目。

　　　         维护线段树。　

         需要注意的是n在线段树中定义为离散后x的最大下标。

 

【代码】

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define FOR(a,b,c) for(int a=(b);a<=(c);a++)
using namespace std;

typedef long long LL;
const int maxn = 400000+10;
const LL MOD = 2147483648LL;
struct Node{
    int x,y;
    bool operator<(const Node& rhs) const{
        return y<rhs.y || (y==rhs.y && x<rhs.x);
    }
}nodes[maxn];

int read() {
    char c=getchar();
    while(!isdigit(c)) c=getchar();
    int x=0;
    while(isdigit(c)) {
        x=x*10+c-'0';
        c=getchar();
    }
    return x;
}
//线段树相关
//+单点修改+区间求和
LL sumv[4*maxn];
int v; LL d;
void update(int u,int L,int R) {
    int lc=u*2,rc=lc+1;
    if(L==R) {
        sumv[u]=d;
    }
    else {
        int M=L+(R-L)/2;
        if(v<=M) update(lc,L,M);
        else update(rc,M+1,R);
        sumv[u]=sumv[lc]+sumv[rc];
    }
}
int y1,y2;
LL query(int u,int L,int R) {
    int lc=u*2,rc=lc+1;
    if(y1<=L && R<=y2) {
        return sumv[u];
    }
    else {
        int M=L+(R-L)/2;
        LL res=0;
        if(y1<=M) res += query(lc,L,M);
        if(M<y2)  res += query(rc,M+1,R);
        res %= MOD;
        return res;
    }
}
//组合函数相关 
LL C[maxn][20];
void get_C(int n) {
    C[0][0]=1;
    for(int i=1;i<=n;i++) {
        C[i][0]=C[i][i]=1;
        for(int j=1;j<=10;j++)
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%MOD;
    }
}

int cx[maxn],sumx[maxn],sumy[maxn];
int hash[5*maxn],x[maxn],y[maxn];
int n,m,w,k;

int main() {
    n=read(),m=read(),w=read();
    get_C(w);
    int p=1;
    FOR(i,1,w) {
        x[i]=read(),y[i]=read();
        hash[p++]=x[i],hash[p++]=y[i];
    }
    p--;
    k=read();
    //离散化坐标 
    sort(hash+1,hash+p+1);
    p=unique(hash+1,hash+p+1)-hash; p--;
    n=0;
    FOR(i,1,w) {
        x[i]=lower_bound(hash+1,hash+p+1,x[i])-hash;
        y[i]=lower_bound(hash+1,hash+p+1,y[i])-hash;
        n=max(n,x[i]);                                     //n用于线段树表示最大x下标 
        sumx[x[i]]++,sumy[y[i]]++;
        nodes[i]=(Node){x[i],y[i]};
    }
    sort(nodes+1,nodes+w+1);
    //扫描每一棵树 
    LL ans=0,cy=0;
    FOR(i,1,w) {
        int r=nodes[i].x,c=nodes[i].y;
        if(i>1 && c==nodes[i-1].y) {
            y1=nodes[i-1].x+1,y2=nodes[i].x-1;
            if(y1<=y2) ans = (ans+C[cy][k]*C[sumy[c]-cy][k]%MOD*query(1,1,n)%MOD)%MOD;
            cy++;
        }
        else cy=1;
        
        cx[r]++;
        v=r; d=C[cx[r]][k]*C[sumx[r]-cx[r]][k]%MOD;
        update(1,1,n);
    }
    printf("%lld\n",ans);
    return 0;
}