算法--数组、链表、栈、队列

一、数组

1、删除有序数组中的重复项（简单）

题目地址：https://leetcode.cn/problems/remove-duplicates-from-sorted-array/

给你一个 升序排列 的数组 nums ，请你原地删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有断言都通过，那么您的题解将被通过。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列

解答

主要使用双指针

class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums == null || nums.length == 0 || nums.length==1){
            return nums.length;
        }
        int j = 0;
        for(int i =1; i< nums.length; i++){
            if(nums[i] != nums[j]){
                nums[++j] = nums[i];
            }
        }
        return j+1;
    }
}

2、移动零（简单）

题目地址：https://leetcode.cn/problems/move-zeroes/

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

提示:

1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1

解答

仍然使用双指针即可

class Solution {
    public void moveZeroes(int[] nums) {
        int j = 0;
        for(int i=0; i<nums.length; i++){
            if(nums[i] != 0){
                nums[j] = nums[i];
                j++;
            }
        }
        while(j < nums.length){
            nums[j++] = 0;
        }
    }
}

3、合并两个有序数组（简单）

题目地址：https://leetcode.cn/problems/merge-sorted-array/

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

解答

这道题仍然使用双指针，还有一个重要的点，就是从后往前循环，这样不会涉及数据的移动，时间复杂度为O(n+m)，如果从前往后循环，会存在单个数组中中间插入的情况，时间复杂度为O(n+logn*m)

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m-1, j = n-1, k = m+n-1;
        while(j >= 0){
            if(i < 0){
                nums1[k--] = nums2[j--];
                continue;
            }
            if(nums1[i] >= nums2[j]){
                nums1[k--] = nums1[i--];
            }else{
                nums1[k--] = nums2[j--];
            }
        }
    }
}

4、加一（简单）

题目地址：https://leetcode.cn/problems/plus-one/description/

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1：

输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

示例 2：

输入：digits = [4,3,2,1]
输出：[4,3,2,2]
解释：输入数组表示数字 4321。

示例 3：

输入：digits = [0]
输出：[1]

提示：

1 <= digits.length <= 100
0 <= digits[i] <= 9

解答

class Solution {
    public int[] plusOne(int[] digits) {
        int j = 0;
        int k = 0;
        for(int i=digits.length-1; i>= 0;i--){
            k = i == digits.length-1 ? 1 : 0;
            int sum = digits[i] + j + k;
            if(sum == 10){
                digits[i] = 0;
                j = 1;
            }else{
                digits[i] = sum;
                j = 0;
                break;
            }
        }
        if(j != 0){
            digits = new int[digits.length+1];
            digits[0] = 1;
        }
        return digits;
    }
}

二、链表

1、反转链表（简单）

题目地址：https://leetcode.cn/problems/reverse-linked-list/

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

解答

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode preNode = head;
        ListNode node = head.next;
        preNode.next = null;
        while(node != null){
            ListNode nextNode = node.next;
            node.next = preNode;
            preNode = node;
            node = nextNode;
        }
        return preNode;
    }
}

2、K 个一组翻转链表（困难）

题目地址：https://leetcode.cn/problems/reverse-nodes-in-k-group/description/

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

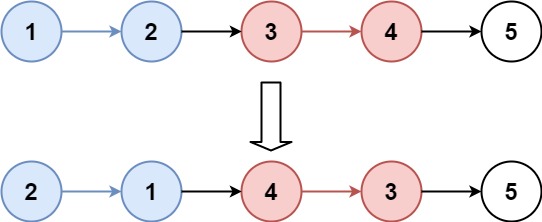
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

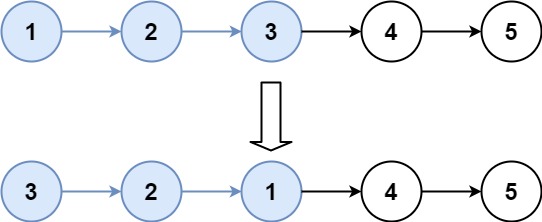
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

解答

解题思路：

1、先分组

2、对于每一组进行翻转

3、对组进行前后关系设置

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode protectNode = new ListNode(0, head);
        ListNode preHead = protectNode;
        while(head != null){
            ListNode end = getEndNode(head, k);
            if(end == null){
                break;
            }
            ListNode nextHead = end.next;
            reverse(head, nextHead);
            preHead.next = end;
            head.next = nextHead;
            preHead = head;
            head = nextHead;
        }
        return protectNode.next;
    }

    private ListNode getEndNode(ListNode head, int k){
        int i=1;
        while(i<k && head != null){
            head = head.next;
            i++;
        }
        return head;
    }

    private void reverse(ListNode head, ListNode end){
        ListNode pre = null;
        while(head != null && head != end){
            ListNode temp = head.next;
            head.next = pre;
            pre = head;
            head = temp;
        }
    }
}

3、环形链表（简单）

题目地址：https://leetcode.cn/problems/linked-list-cycle/description/

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。

进阶：你能用 O(1)（即，常量）内存解决此问题吗？

解答

主要用到快慢指针，如果快慢指针走到同一个位置，说明有循环链表，否则就不存在

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
            if(fast == slow){
                return true;
            }
        }
        return false;
    }
}

4、环形链表2（中等）

题目地址：https://leetcode.cn/problems/linked-list-cycle-ii/description/

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引

进阶：你是否可以使用 O(1) 空间解决此题？

解答

这道题主要是解题思路，代码并不难

首先定义几个变量，x：表示环形链表前的长度，y：表示从环形链表开始到快慢指针相遇的长度，r：表示环形链表的长度

那么，快指针走的长度为：fast = x + mr+y，满指针走的长度为：slow= x + nr+y，其中m和n分别表示快慢指针循环环形链表的次数

由于快指针走的速度是满指针的2倍，因此就有 fast = 2slow，移动后 x = (m-2n)r - y，也就是从环形链表相遇的节点开始到环形链表的开始节点的长度与链表头结点到环形链表节点开始节点长度一致

基于以上分析，解题思路如下：

1、首先使用快慢指针找到相同节点

2、再用两个指针，一个从环形链表相遇节点往后递进，一个从链表头结点向前递进，最终汇合的节点就是环形链表的开始节点

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        ListNode meetNode = null;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
            if(fast == slow){
                meetNode = fast;
                break;
            }
        }
        if(meetNode == null){
            return null;
        }
        while(meetNode != head){
            head = head.next;
            meetNode = meetNode.next;
        }
        return meetNode;

    }
}

5、合并两个有序链表（简单）

题目地址：https://leetcode.cn/problems/merge-two-sorted-lists/description/

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

解答：

比较简单，就不做说明了，这里说一个易错点，while(list1 != null || list2 != null)特别容易写成while(list1 != null && list2 != null)，需要注意

另外可以把 if(list1 == null){ 与 if(list1.val <= list2.val) 合并到一个分支为 if(list2 == null || (list1 != null && list1.val <= list2.val))，不过这样如果 list2 为 null，仍然需要循环 list1 的长度，如果直接设置完 break，就不需要循环。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode protectNode = new ListNode();
        ListNode head = protectNode;
        while(list1 != null || list2 != null){
            if(list1 == null){
                head.next = list2;
                break;
            }
            if(list2 == null){
                head.next = list1;
                break;
            }
            if(list1.val <= list2.val){
                head.next = list1;
                ListNode temp = list1.next;
                list1.next = null;
                list1 = temp;
            }else{
                head.next = list2;
                ListNode temp = list2.next;
                list2.next = null;
                list2 = temp;
            }
            head = head.next;
        }
        return protectNode.next;
    }
}

三、栈与队列

0、概述

栈对先进后出，队列时先进先出，比较简单，没什么可说的

1、有效的括号（简单）

题目地址：https://leetcode.cn/problems/valid-parentheses/

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

提示：

1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成

解答

使用栈先进先出的特性

class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack();
        for(char c : s.toCharArray()){
            if(c == '(' || c== '[' || c == '{'){
                stack.push(c);
            }else{
                if(stack.isEmpty()){
                    return false;
                }
                char top = stack.pop();
                if(c == ')' && '(' != top 
                    || c == ']' && '[' != top
                    || c == '}' && '{' != top){
                    return false;
                }
            }
        }
        return stack.isEmpty();
    }
}

2、最小栈（中等）

题目地址：https://leetcode.cn/problems/min-stack/description/

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

-231 <= val <= 231 - 1
pop、top 和 getMin 操作总是在 非空栈 上调用
push, pop, top, and getMin最多被调用 3 * 104 次

解答

要求最小值，那么就需要额外的空间进行存储，就定义一个 minStack

最小值栈的存储，每一次 push 时，都记录当前的最小值，例如上面的 -2，0，-3 的顺序

push -2 时，最小值栈为空，最小值为 -2

push 0 时，最小值为 -2

push -3 时，最小值为 -3

因此就可以定义一个最小值栈，每一次 push 时，存储的是原栈中的最小值，那么每一次 pop 原栈时，就需要把最小值栈也 pop 一次。

注：之前想过使用三个栈，原栈还存在，另外有一个最小值栈和一个临时栈，临时栈完全作为新来数据时，最小值栈为了重新排序而设定的一个临时存储空间。这样思路也没问题，但是当代码提交时，提示超出了运行时间，看来这样方式的效率还是不行。

class MinStack {
    private Stack<Integer> stack;
    private Stack<Integer> minStack;


    public MinStack() {
        stack = new Stack();
        minStack = new Stack();
    }
    
    public void push(int val) {
        stack.push(val);
        val = minStack.isEmpty() ? val : Math.min(val, minStack.peek());
        minStack.push(val);
    }
    
    public void pop() {
        stack.pop();
        minStack.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

3、逆波兰表达式求值（中等）

题目地址：https://leetcode.cn/problems/evaluate-reverse-polish-notation/description/

根据逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

注意两个整数之间的除法只保留整数部分。

可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

1 <= tokens.length <= 104
tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

解答

用到了栈，如果不是运算符，就往栈里添加，如果是运算符，就从栈里面获取两个数据进行运算，再把运算结果放入栈中

易错点：pop 的时候要注意两个值的先后顺序，第一个 pop 的是运算符后面的数据，第二个 pop 的数据是运算符前面的数据，对于减法和除法要特别注意。

class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> numStack = new Stack();
        for(String s : tokens){
            if(s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")){
                int y = numStack.pop();
                int x = numStack.pop();
                if(s.equals("+")){
                    numStack.push(x + y);
                }
                if(s.equals("-")){
                    numStack.push(x - y);
                }
                if(s.equals("*")){
                    numStack.push(x * y);
                }
                if(s.equals("/")){
                    numStack.push(x / y);
                }
            }else{
                numStack.push(Integer.parseInt(s));
            }
        }
        return numStack.pop();
    }
}

4、面试题 16.26. 计算器（中等）

题目地址：https://leetcode.cn/problems/calculator-lcci/description/

给定一个包含正整数、加(+)、减(-)、乘(*)、除(/)的算数表达式(括号除外)，计算其结果。

表达式仅包含非负整数，+， - ，*，/ 四种运算符和空格。整数除法仅保留整数部分。

示例 1:

输入: "3+2*2"
输出: 7

示例 2:

输入: " 3/2 "
输出: 1

示例 3:

输入: " 3+5 / 2 "
输出: 5

说明：

你可以假设所给定的表达式都是有效的。
请不要使用内置的库函数 eval。

解答

解题思路：

1、中缀转后缀：可以将中缀表达式改为后缀表达式，即上面的逆波兰表达式，就是将运算符放入两个需要运算的数据之后，然后出一个运算符，就接着出两个数字，运算完毕后将数据再让进去。

2、定义两个栈分别存储数字和运算符：那么为了更好的获取数字和获取运算符，就需要使用两个栈，一个存储数据，一个存储运算符，即循环字符，如果是数字的就放入数字的栈，如果是运算符的就放入运算符的栈

3、运算符优先级：由于运算符有优先级，因此不能无脑的将数字和运算符放入栈中，如果新来的运算符优先级小于等于栈中已有的优先级，则先将栈中的运算符计算

4、最后出栈：在全部循环完毕后，有可能符号栈中还有运算符没有出栈，因此需要再判断将运算符栈中数据出栈完

5、结束控制：由于可能出现两位及以上的数字，因此在判断数字时，使用的是字符判断，每次和之前的相加，直到遇到非数字才停止，并将该数字入栈，那么就存在最后一个数字没法入栈的情况；另外题目中提示可能有空格，那么就取个巧，在字符串的最后加上一个空格，保证最后一个数值可以入栈。

取巧点：字符串后加空格保证最后一个数值入栈

易错点：在判断符号优先级时，有两个点容易出错：

1、第一个是优先级的判断，必须是前面的优先级大于等于当前准备入栈的优先级，就需要先计算前面的结果，必须包含等于，因为不包含的话，就可能出现 1-1+1=-1的情况（因为这两个服务的优先级一样，没有先做前面的运算，而都放入了栈中，最后使用后缀表达式，先算后面再算前面）

2、第二个 for 循环中的 while，这里比较容易被误用 if，如果使用 if，就可能出现 2-3/4+5=-3的情况，因为 if 只判断一次，那么第一个减号，直接入栈，第二个除号，比之前的优先极高，也入栈，到了加号，比之前的优先级低，那么优先算 3/4，但是由于 if 只判断了一次，就会变为 2-0+5，根据后缀表达式，就会产生 -3 的结果，使用 while 可以一直向前判断，在 3/4 算完后，继续使用加号和之前的运算符比较（减号），仍然是小于等于，那么之前的继续运算，最后就会得到 2+5 ，最终值为7

class Solution {
    public int calculate(String s) {
        Stack<Integer> numStack = new Stack();
        Stack<Character> opsStack = new Stack();
        s += " ";
        String numStr = "";
        for(char ch : s.toCharArray()){
            if(ch >= '0' && ch <= '9'){
                numStr += ch;
                continue;
            }else if(!"".equals(numStr)){
                numStack.push(Integer.parseInt(numStr));
                numStr = "";
            }
            if(ch == ' '){
                continue;
            }
            while(!opsStack.isEmpty() && getRange(opsStack.peek()) >= getRange(ch)){
                numStack.push(grtResult(numStack.pop(), numStack.pop(), opsStack.pop()));
            }
            opsStack.push(ch);
        }
        while(!opsStack.isEmpty()){
            numStack.push(grtResult(numStack.pop(), numStack.pop(), opsStack.pop()));
        }
        return numStack.pop();
    }

    private int getRange(char ch){
        if(ch == '*' || ch == '/'){return 2;}
        if(ch == '+' || ch == '-'){return 1;}
        return 0;
    }

    private int grtResult(int val1, int val2, char ops){
        if(ops == '+'){return val2 + val1;}
        if(ops == '-'){return val2 - val1;}
        if(ops == '*'){return val2 * val1;}
        return val2 / val1;
    }
}

5、基本计算器（困难）

题目地址：https://leetcode.cn/problems/basic-calculator/description/

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

注意:不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "1 + 1"
输出：2

示例 2：

输入：s = " 2-1 + 2 "
输出：3

示例 3：

输入：s = "(1+(4+5+2)-3)+(6+8)"
输出：23

提示：

1 <= s.length <= 3 * 105
s 由数字、'+'、'-'、'('、')'、和 ' ' 组成
s 表示一个有效的表达式
'+' 不能用作一元运算(例如， "+1" 和 "+(2 + 3)" 无效)
'-' 可以用作一元运算(即 "-1" 和 "-(2 + 3)" 是有效的)
输入中不存在两个连续的操作符
每个数字和运行的计算将适合于一个有符号的 32位整数

解答

这道题和上面题有两个大的区别，一个是有括号，一个是可能存在负号，而上面的题有乘除，这道题没有，则不用考虑，那么直接把上面问题的解答拿下来，针对这两个大的区别点做针对的修改。

1、有括号：主要添加对于括号的判断，如果是左括号，直接放入符号栈中，如果是右括号，则直接向前进行处理，直到遇到一个左括号

2、负值：其实这道题出的有问题，并没有描述存在负号的情况，但是在提交的时候会又能相关的测试用例，导致提交不成功。

对于负号的问题，可以通过在负号前补零来处理，那么就要看哪些场景需要补零了。

补零的场景：如果负号在左括号后面，或者在加减号后面，都是需要补零的，那么就可以设置一个标志，在这两个场景时，将该标志设置为true，但是如果实在数字之后，就不需要补零。

标记设置完成后，如果需要补零，并且当前符号为符号，那就需要在前面补零，即往数值栈中添加一个零。

class Solution {
    public int calculate(String s) {
        Stack<Integer> numStack = new Stack();
        Stack<Character> opsStack = new Stack();
        s += " ";
        String numStr= "";
        boolean needZero = true;
        for(char ch : s.toCharArray()){
            if(ch >= '0' && ch <= '9'){
                numStr += ch;
                needZero = false;
                continue;
            }else if(!"".equals(numStr)){
                numStack.push(Integer.parseInt(numStr));
                numStr = "";
            }
            if(ch == ' '){
                continue;
            }
            if(ch == '('){
                opsStack.push(ch);
                needZero = true;
                continue;
            }
            if(ch == ')') {
                while(opsStack.peek() != '('){
                    numStack.push(getResult(numStack.pop(), numStack.pop(), opsStack.pop()));
                }
                opsStack.pop();
                continue;
            }
            if(ch == '-' && needZero){
                numStack.push(0);
            }
            while(!opsStack.isEmpty() && getRange(ch) <= getRange(opsStack.peek())){
                numStack.push(getResult(numStack.pop(), numStack.pop(), opsStack.pop()));
            }
            needZero = true;
            opsStack.push(ch);
        }
        while(!opsStack.isEmpty()){
            numStack.push(getResult(numStack.pop(), numStack.pop(), opsStack.pop()));
        }
        return numStack.pop();
    }

    private int getRange(char ch){
        if(ch == '+' || ch == '-') {return 1;}
        if(ch == '*' || ch == '/') {return 2;}
        return 0;
    }

    private int getResult(int v1, int v2, char ops){
        if(ops == '+') { return v2 + v1;}
        if(ops == '-') { return v2 - v1;}
        if(ops == '*') { return v2 * v1;}
        return v2 / v1;
    }
}

7、设计循环双端队列（中等）

题目地址：https://leetcode.cn/problems/design-circular-deque/

设计实现双端队列。

实现 MyCircularDeque 类:

MyCircularDeque(int k) ：构造函数,双端队列最大为 k 。
boolean insertFront()：将一个元素添加到双端队列头部。如果操作成功返回 true ，否则返回 false 。
boolean insertLast() ：将一个元素添加到双端队列尾部。如果操作成功返回 true ，否则返回 false 。
boolean deleteFront() ：从双端队列头部删除一个元素。如果操作成功返回 true ，否则返回 false 。
boolean deleteLast() ：从双端队列尾部删除一个元素。如果操作成功返回 true ，否则返回 false 。
int getFront() )：从双端队列头部获得一个元素。如果双端队列为空，返回 -1 。
int getRear() ：获得双端队列的最后一个元素。如果双端队列为空，返回 -1 。
boolean isEmpty() ：若双端队列为空，则返回 true ，否则返回 false 。
boolean isFull() ：若双端队列满了，则返回 true ，否则返回 false 。

示例 1：

输入
["MyCircularDeque", "insertLast", "insertLast", "insertFront", "insertFront", "getRear", "isFull", "deleteLast", "insertFront", "getFront"]
[[3], [1], [2], [3], [4], [], [], [], [4], []]
输出
[null, true, true, true, false, 2, true, true, true, 4]

解释
MyCircularDeque circularDeque = new MycircularDeque(3); // 设置容量大小为3
circularDeque.insertLast(1);			        // 返回 true
circularDeque.insertLast(2);			        // 返回 true
circularDeque.insertFront(3);			        // 返回 true
circularDeque.insertFront(4);			        // 已经满了，返回 false
circularDeque.getRear();  				// 返回 2
circularDeque.isFull();				        // 返回 true
circularDeque.deleteLast();			        // 返回 true
circularDeque.insertFront(4);			        // 返回 true
circularDeque.getFront();				// 返回 4

提示：

1 <= k <= 1000
0 <= value <= 1000
insertFront, insertLast, deleteFront, deleteLast, getFront, getRear, isEmpty, isFull 调用次数不大于 2000 次

解答：

没什么可说的

class MyCircularDeque {
    ListNode headNode;
    ListNode endNode;
    int count;
    int limit;
    public MyCircularDeque(int k) {
        headNode = new ListNode();
        endNode = new ListNode();
        headNode.next = endNode;
        endNode.pre = headNode;
        count = 0;
        limit = k;
    }
    
    public boolean insertFront(int value) {
        if(count == limit){
            return false;
        }
        count += 1;
        ListNode tempNode = headNode.next;
        ListNode thisNode = new ListNode(value);
        headNode.next = thisNode;
        thisNode.pre = headNode;
        thisNode.next = tempNode;
        tempNode.pre = thisNode;
        return true;
    }
    
    public boolean insertLast(int value) {
        if(count == limit){
            return false;
        }
        count += 1;
        ListNode tempNode = endNode.pre;
        ListNode thisNode = new ListNode(value);
        tempNode.next = thisNode;
        thisNode.pre = tempNode;
        thisNode.next = endNode;
        endNode.pre = thisNode;
        return true;
    }
    
    public boolean deleteFront() {
        if(count == 0){
            return false;
        }
        count -= 1;
        ListNode tempNode = headNode.next.next;
        headNode.next = tempNode;
        tempNode.pre = headNode;
        return true;
    }
    
    public boolean deleteLast() {
        if(count == 0){
            return false;
        }
        count -= 1;
        ListNode tempNode = endNode.pre.pre;
        endNode.pre = tempNode;
        tempNode.next = endNode;
        return true;
    }
    
    public int getFront() {
        return count == 0 ? -1 : headNode.next.val;
    }
    
    public int getRear() {
        return count == 0 ? -1 : endNode.pre.val;
    }
    
    public boolean isEmpty() {
        return count == 0;
    }
    
    public boolean isFull() {
        return count == limit;
    }
}

class ListNode{
    public ListNode next;
    public ListNode pre;
    public int val;

    public ListNode(int val){
        this.val = val;
    }

    public ListNode(){

    }
}
/**
 * Your MyCircularDeque object will be instantiated and called as such:
 * MyCircularDeque obj = new MyCircularDeque(k);
 * boolean param_1 = obj.insertFront(value);
 * boolean param_2 = obj.insertLast(value);
 * boolean param_3 = obj.deleteFront();
 * boolean param_4 = obj.deleteLast();
 * int param_5 = obj.getFront();
 * int param_6 = obj.getRear();
 * boolean param_7 = obj.isEmpty();
 * boolean param_8 = obj.isFull();
 */

四、单调栈与单调队列

0、概述

单调队列和单调栈并非一种数据结构，而是为了解题而出现的一种思路，将不规则的线性结构转变为单调递增或者单调递减的规则线性结构，进而可以更好计算结果。

单调栈和单调队列的解题套路：

（1）for 循环每一个选项

（2）while（栈顶与新元素不满足单调性）{弹栈，更新答案，累加"宽度"}

（3）入栈

1、柱状图中最大的矩形（困难）

题目地址：https://leetcode.cn/problems/largest-rectangle-in-histogram/

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

输入： heights = [2,4]
输出： 4

提示：

1 <= heights.length <=105
0 <= heights[i] <= 104

解答

解题思路：

1、为什么选择单调栈：如果数组（柱子）是单调递增，那么就比较好处理：

如果从左开始，第 i 跟柱子时，height*（length-i），那么循环每一根柱子，在每一跟柱子时计算面积，然后和既往最大值对比即可

其中 i 为当前节点的位置，length 为数组长度，height 为第 i 跟柱子的高度

如果从右开始，计算出当前节点的面积后，将高度设置为和前面的高度一致，再计算前面的高度

2、如何变为单调栈

这里选择单调递增，那么就是循环数组，如果当前节点满足单调性，就入栈，如果不满足单调性，就进行处理（根据具体的题意进行处理，修正、抛弃、调整前一个等）让其单调性成立，在这道题里，就把之前满足的做一个处理，保证之前节点的高度都小于当前节点的高度

由于是要计算最大面积，因此之前的抛弃时，要先计算之前的面积，例如现在是 2,3,4,1，那么在 1 这个节点

之前的4已经不满足单调性，那么就应该把 4 抛弃，但是需要计算一下当前节点的最大面积，高度为4，宽度为1，面积为4

再继续，3也不满足单调性，抛弃3，在这时，高为3，宽为2（因为之前的4虽然抛弃，但是宽度仍然在），面积为6

再继续，2也不满足单调性，抛弃2，在这时，高为2，宽为3，面积为6

最终 2,3,4 都被抛弃，需要将 1 放入栈，放入的是高为 1，宽为 4 的节点（宽需要加上之前抛弃的所有节点的宽）

3、特殊处理

上面方法实际是保证了栈的单调性，但是最终的数据没有处理，例如最终的单调栈为 2,3,4,5，那么都是push到栈中了，并没有计算最大值，或者没有计算完毕，就需要从前或者从后再计算一遍。

为了避免上述再来一次循环导致代码臃肿，可以取个巧，就是在数组的最后加一个0，让其在最后的节点不满足单调性，就会把之前的都计算了，所以，在 for 循环的判断里，使用了 i<= heights.leng 的条件（加上了等号），并且取第 i 个节点的高度时，如果是第 heights.length时，height 设置为 0，让其前面的所有都不满足单调性。

class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack<Rect> stack = new Stack();
        int ans = 0;
        for(int i=0;i<= heights.length;i++){
            int height = i== heights.length ? 0 : heights[i];
            int sumWeight = 0;
            while(!stack.isEmpty() && stack.peek().height >= height){
                Rect rect = stack.pop();
                sumWeight += rect.weight;
                ans = Math.max(ans, sumWeight*rect.height);
            }
            stack.push(new Rect(sumWeight+1, height));
        }
        return ans;
    }
}

class Rect{
    public int weight;
    public int height;

    public Rect(int weight, int height){
        this.weight = weight;
        this.height = height;
    }
}

2、滑动窗口最大值（困难）

题目地址：https://leetcode.cn/problems/sliding-window-maximum/

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length

解答

题目分析：

以示例1为例，循环每一个节点：

i=0，值为1，可能最大值为1

i=1，值为3，由于1和3肯定在一组，因此1就没有作用，最大值为3

i=2，值为-1，由于可能存在1,3,-1,-2,-3的情况，因此-1有可能成为后续的最大值

i=3，值为-3，与上面一样，可能存在其为最大值的情况

i=4，值为5，那么往前推两位（k=3），前面两位分别是-1和-3，那么-1和-3就不可能成为最大值

综上分析，如果使用一个单调队列，保证其为单调递减，那么每一个节点都有可能成为后续的最大值，这个队列是从后面添加数据的，但是还要保证取数据的区间为k的限制，如果头结点的位置超过了当前节点与k的范围，就要移除，也就是说，从而保证一定取到的是k范围内的最大值。

解题：

由于要从两端操作单调栈，那么就可以使用一个双端队列，同时为了判断最大值的位置，则双端队列中存储的是最大值的下标，同时单调栈中保持单调递减，那么套用单调栈的套路，解题思路如下：
for 循环

如果单调栈中的头结点超出了范围，就剔除头结点

while 判断，对于不满足单调性的节点处理，使其满足单调性

获取头结点放入结果集

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] ans = new int[nums.length-k+1];
        Deque<Integer> deque = new LinkedList();
        for(int i=0;i<nums.length;i++){
            if(!deque.isEmpty() && i-k >= deque.getFirst()){
                deque.removeFirst();
            }
            while(!deque.isEmpty() && nums[deque.getLast()] <= nums[i]){
                deque.removeLast();
            }
            deque.addLast(i);
            if(i>=k-1){
                ans[i-k+1] = nums[deque.getFirst()];
            }
        }
        return ans;
    }
}

3、接雨水（困难）

题目地址：https://leetcode.cn/problems/trapping-rain-water/

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

解答1：单调栈

分析思路：雨水可以向左或向右流动，直到碰到比他高的节点就会停止，如果两端都碰到比他高的节点，那么当前节点的水就能被收集，如果是这样，保证单调递减，那么从第二个节点开始，都是有盛水的可能的，那么如果碰到了不满足单调递减的节点，就可以去计算一次盛水量，因此本题可以采用单调递减的方式处理。

解题套路仍然一样，先循环所有节点，如果满足单调性，则push，不满足单调性，则针对该题的特殊场景做处理

不满足单调性处理：不满足单调性，说明前一个节点比当前节点低，那么就要算出来前一个节点能存多少水，公式为：(Math.min(stack.peek().height, height) - rect.height) * sumWeight，其中stack.peek().height表示要前一个节点再之前一个节点的高度，height表示当前节点的高度，rect.height表示前一个节点的高度，sumWeight表示前一个节点的宽度。

可能描述起来比较绕口，举例，5,3,6这个场景，到了6，是不满足单调性的，因此就要计算当前节点（6）之前节点（3）可以盛多少水，那么其可以盛3左右高低低的那一个，然后再减去3本身的高度，就可以计算其盛水高度，宽度即为3这个节点本身的宽度。

class Solution {
    public int trap(int[] heights) {
        Stack<Rect> stack = new Stack();
        int ans = 0;
        for(int height : heights){
            int sumWeight = 0;
            while(!stack.isEmpty() && stack.peek().height <= height){
                Rect rect = stack.pop();
                if(stack.isEmpty()){
                    continue;
                }
                sumWeight += rect.weight;
                ans += (Math.min(stack.peek().height, height) - rect.height) * sumWeight;
            }
            stack.push(new Rect(sumWeight+1, height));
        }
        return ans;
    }

}

class Rect{
    public int weight;
    public int height;

    public Rect(int weight, int height){
        this.weight = weight;
        this.height = height;
    }
}

解答2：前缀最大值

一个更好理解的观点：到一个节点后，查看其前后的最大值，那么最大值中的最小值如果大于当前节点的高度，则可以盛水，盛水的容量为左右最大值的小者与当前节点的高度差。

    public int trap(int[] heights) {
        int ans = 0;
        int[] preMax = new int[heights.length];
        int[] suffMax = new int[heights.length];
        for(int i=1;i<heights.length;i++){
            preMax[i] = Math.max(preMax[i-1], heights[i-1]);
        }
        for(int i = heights.length-2;i>=0;i--){
            suffMax[i] = Math.max(suffMax[i+1], heights[i+1]);
            System.out.println(suffMax[i]);
        }
        for(int i=1;i<heights.length-1;i++){
            if(suffMax[i] > heights[i] && preMax[i] > heights[i]){
                ans += Math.min(suffMax[i], preMax[i]) - heights[i];
            }
        }
        return ans;
    }

4、最大矩形（困难）

题目地址：https://leetcode.cn/problems/maximal-rectangle/

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [["0"]]
输出：0

示例 4：

输入：matrix = [["1"]]
输出：1

示例 5：

输入：matrix = [["0","0"]]
输出：0

提示：

rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 '0' 或 '1'

解答

这道题是第一题的一个扩展，循环每一行，将每一行变更为柱形数组即可，那么解题思路就变成了以下三步

1、循环每一行，将每一行变为一个柱形数组：int[] heights = geneHeight(i, matrix);

2、计算每一行柱形数组能得到的最大面积：max = getMax(heights)

3、比较每一行的最大面积，从主取出最大值：ans = Math.max(ans, max)

第2点，完成照搬第一题即可，第三点没什么可说的，就单独说一下第一点

循环每一列，行都是从固定行开始，如果当前列的当前行不为1，当前柱形的高就加一，然后继续向上递归，直到碰到0或者到了第一行，就计算出了当前列的高。

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int ans = 0;
        for(int i=0;i<matrix.length;i++){
            int[] heights = geneHeight(i, matrix);
            ans = Math.max(ans, getMax(heights));
        }
        return ans;
    }

    private int[] geneHeight(int row, char[][] matrix){
        int col = matrix[row].length;
        int[] heights = new int[col];
        for(int i=0; i<col; i++){
            int height = 0;
            int rowTemp = row;
            while(rowTemp >=0 && matrix[rowTemp][i] != '0'){
                height++;
                rowTemp--;
            }
            heights[i] = height;
        }
        return heights;
    }

    private int getMax(int[] heights){
        Stack<Rect> stack = new Stack();
        int ans = 0;
        for(int i=0; i<=heights.length;i++){
            int height = i == heights.length ? 0 : heights[i];
            int sumWeight = 0;
            while(!stack.isEmpty() && stack.peek().height >= height){
                Rect rect = stack.pop();
                sumWeight += rect.weight;
                ans = Math.max(ans, sumWeight*rect.height);
            }
            stack.push(new Rect(sumWeight+1, height));
        }
        return ans;
    }
}


class Rect{
    public int weight;
    public int height;

    public Rect(int weight, int height){
        this.weight = weight;
        this.height = height;
    }
}

posted @ 2022-12-03 15:20 李聪龙阅读(33) 评论(0) 编辑收藏举报

刷新页面返回顶部

朦胧的夜~

算法--数组、链表、栈、队列

一、数组

1、删除有序数组中的重复项（简单）

解答

2、移动零（简单）

解答

3、合并两个有序数组（简单）

解答

4、加一（简单）

解答

二、链表

1、反转链表（简单）

解答

2、K 个一组翻转链表（困难）

解答

3、环形链表（简单）

解答

4、环形链表2（中等）

解答

5、合并两个有序链表（简单）

解答：

三、栈与队列

0、概述

1、有效的括号（简单）

解答

2、最小栈（中等）

解答

3、逆波兰表达式求值（中等）

解答

4、面试题 16.26. 计算器（中等）

解答

5、基本计算器（困难）

解答

7、设计循环双端队列（中等）

解答：

四、单调栈与单调队列

0、概述

1、柱状图中最大的矩形（困难）

解答

2、滑动窗口最大值（困难）

解答

3、接雨水（困难）

解答1：单调栈

解答2：前缀最大值

4、最大矩形（困难）

解答

公告