由Integer的对比引出对于Integer的思考
一、Integer各场景对比结果
对于Integer各种情况的对比及结果如下代码所示:
@Test public void test() { Integer a = new Integer(2); Integer b = 2; Integer c = 2; int x = 2; log.info("a==b 的结果:{}", a==b);//1、false log.info("a==x 的结果:{}", a==x);//2、true log.info("c==b 的结果:{}", c==b);//3、true log.info("b==x 的结果:{}", x==b);//4、true Integer d = new Integer(150); Integer e = 150; Integer f = 150; int y = 150; log.info("d==e 的结果:{}", d==e);//5、false log.info("d==y 的结果:{}", d==y);//6、true log.info("e==f 的结果:{}", e==f);//7、false log.info("e==y 的结果:{}", e==y);//8、true }
可以逐个解释一下结果的原因,
1:由于a是使用new新开辟的内存空间,因此结果为false;
2、a与x对比时,由于x是基本类型,那么Integer也需要转换为基本类型就行对比,那么就是纯数值的对比,为true
3、c与b对比,结果为true,是因为Integer为了减少内存的使用,因此在缓存中直接缓存了-128~127之间的数值(存储在常量池),只要是在这之间的数据,则直接从缓存中获取(如果是使用new新创建,则是开辟一个新的空间,和场景1一样,结果为false),因此为true
4、与2一样,没什么可说的
对于5~8,其实主要是7的结果,7和3的结果不一样,结果为false,其原因也是和3中说的一样,Integer为了减少内存的使用,缓存了-128~127之间的数值,但是如果不在该范围内的数值,都是需要重新开辟空间的,因此结果为false。
二、Integer取值范围引发对于源码、反码、补码的思考
我们都知道Integer的取值范围是 -2^31 ~ 2^31-1,那么为什么是这样的值,而不是其他的值,或者为什么不是 -2^31 ~ 2^31呢?,这里就涉及到了计算机中的源码、反码、补码了。
(一)机器数与真值
在学习原码,反码和补码之前, 需要先了解机器数和真值的概念。
1、机器数
一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是带符号的,在计算机用机器数的最高位存放符号,正数为0,负数为1。
比如,十进制中的数 +3 ,计算机字长为8位,转换成二进制就是0000 0011。如果是 -3 ,就是 100 00011 。
2、机器数的真值
因为第一位是符号位,所以机器数的形式值就不等于真正的数值。
例如上面的有符号数 1000 0011,其最高位1代表负,其真正数值是 -3,而不是形式值131(1000 0011转换成十进制等于131)。所以,为区别起见,将带符号位的机器数对应的真正数值称为机器数的真值。
例:0000 0001的真值 = +000 0001 = +1,1000 0001的真值 = –000 0001 = –1
(二)原码, 反码, 补码的基础概念和计算方法
在探求为何机器要使用补码之前,让我们先了解原码、反码和补码的概念。对于一个数,计算机要使用一定的编码方式进行存储,原码、反码、补码是机器存储一个具体数字的编码方式。
1. 原码
原码就是符号位加上真值的绝对值,即用第一位表示符号,其余位表示值。比如:如果是8位二进制:[+1]原= 0000 0001 [-1]原= 1000 0001
第一位是符号位,因为第一位是符号位,所以8位二进制数的取值范围就是:(即第一位不表示值,只表示正负。);[1111 1111 , 0111 1111]即[-127 , 127]
原码是人脑最容易理解和计算的表示方式。
2. 反码
反码的表示方法是:
正数的反码是其本身;负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
[+1] = [0000 0001]原= [0000 0001]反;[-1] = [1000 0001]原= [1111 1110]反
可见如果一个反码表示的是负数,人脑无法直观的看出来它的数值。通常要将其转换成原码再计算。
3. 补码
补码的表示方法是:
正数的补码就是其本身;
负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1。(也即在反码的基础上+1)
[+1] = [0000 0001]原= [0000 0001]反= [0000 0001]补;[-1] = [1000 0001]原= [1111 1110]反= [1111 1111]补
对于负数,补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码再计算其数值。
(三)为何要使用原码、反码和补码
在开始深入学习前,我的学习建议是先"死记硬背"上面的原码,反码和补码的表示方式以及计算方法。
现在我们知道了计算机可以有三种编码方式表示一个数,对于正数因为三种编码方式的结果都相同:
[+1] = [0000 0001]原= [0000 0001]反= [0000 0001]补
所以不需要过多解释,但是对于负数:
[-1] = [10000001]原= [11111110]反= [11111111]补
可见原码,反码和补码是完全不同的。既然原码才是被人脑直接识别并用于计算表示方式,为何还会有反码和补码呢?
首先, 因为人脑可以知道第一位是符号位,在计算的时候我们会根据符号位,选择对真值区域的加减。(真值的概念在本文最开头) 但是对于计算机,加减乘数已经是最基础的运算,要设计的尽量简单,计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂!
于是人们想出了将符号位也参与运算的方法。我们知道,根据运算法则减去一个正数等于加上一个负数,即:1-1 = 1 + (-1) = 0, 所以机器可以只有加法而没有减法,这样计算机运算的设计就更简单了。
于是人们开始探索将符号位参与运算,并且只保留加法的方法。
首先来看原码:
计算十进制的表达式: 1 - 1 = 0
1 - 1 = 1 + (-1) = [0000 0001]原+ [1000 0001]原= [1000 0010]原= -2
如果用原码表示,让符号位也参与计算,显然对于减法来说,结果是不正确的。这也就是为何计算机内部不使用原码表示一个数。
为了解决原码做减法的问题, 出现了反码:
计算十进制的表达式:1 - 1 = 0
1 - 1 = 1 + (-1) = [0000 0001]原+ [1000 0001]原= [0000 0001]反+ [1111 1110]反= [1111 1111]反= [1000 0000]原= -0
发现用反码计算减法,结果的真值部分是正确的。而唯一的问题其实就出现在"0"这个特殊的数值上,虽然人们理解上+0和-0是一样的,但是0带符号是没有任何意义的,而且会有[0000 0000]原和[1000 0000]原两个编码表示0。
于是补码的出现,解决了0的符号问题以及0的两个编码问题:
1-1 = 1 + (-1) = [0000 0001]原+ [1000 0001]原= [0000 0001]补+ [1111 1111]补= [1 0000 0000]补=[0000 0000]补=[0000 0000]原(注意:进位1不在计算机字长里)
这样0用[0000 0000]表示,而以前出现问题的-0则不存在了。而且可以用[1000 0000]表示-128:-128的由来如下:
(-1) + (-127) = [1000 0001]原+ [1111 1111]原= [1111 1111]补+ [1000 0001]补= [1000 0000]补
-1-127的结果应该是-128,在用补码运算的结果中,[1000 0000]补就是-128,但是注意因为实际上是使用以前的-0的补码来表示-128,所以-128并没有原码和反码表示。(对-128的补码表示[1000 0000]补,算出来的原码是[0000 0000]原,这是不正确的)
使用补码,不仅仅修复了0的符号以及存在两个编码的问题,而且还能够多表示一个最低数。这就是为什么8位二进制,使用原码或反码表示的范围为[-127, +127],而使用补码表示的范围为[-128, 127]。
因为机器使用补码,所以对于编程中常用到的有符号的32位int类型,可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位,而使用补码表示时又可以多保存一个最小值。
(四)原码, 反码, 补码 再深入
计算机巧妙地把符号位参与运算,并且将减法变成了加法,背后蕴含了怎样的数学原理呢?
将钟表想象成是一个1位的12进制数。如果当前时间是6点,我希望将时间设置成4点,需要怎么做呢?我们可以:
1. 往回拨2个小时:6 - 2 = 4
2. 往前拨10个小时:(6 + 10) mod 12 = 4
3. 往前拨10+12=22个小时:(6+22) mod 12 =4
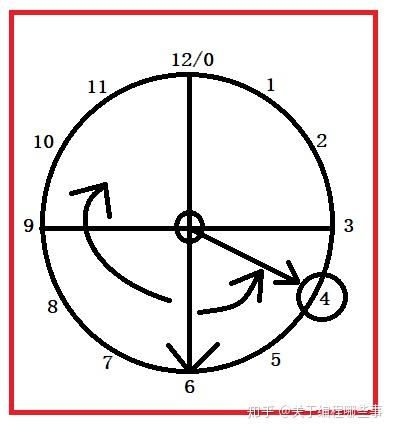
上面2,3方法中的mod是指取模操作,16 mod 12 =4,即用16除以12后的余数是4。
所以钟表往回拨(减法)的结果可以用往前拨(加法)替代!
现在的焦点就落在了如何用一个正数,来替代一个负数呢?上面的例子我们能感觉出来一些端倪,发现一些规律。但是数学是严谨的,不能靠感觉。
首先介绍一个数学中相关的概念:同余
同余的概念
两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余。记作 a ≡ b (mod m),读作 a 与 b 关于模 m 同余。
举例说明:
4 mod 12 = 4;16 mod 12 = 4;28 mod 12 = 4
所以4,16,28对于模 12 同余。
负数取模
正数进行mod运算是很简单的,但是负数呢?
下面是关于mod运算的数学定义:
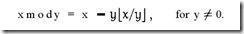
上面是截图,"取下界”符号找不到如何输入(word中粘贴过来后乱码)。下面是使用 [ 和 ) 替换上图的"取下界"符号:
x mod y = x - y [ x / y )
上面公式的意思是:x mod y等于 x 减去 y 乘上 x与y的商的下界。
以 -3 mod 2 举例: -3 mod 2 = -3 - 2x[ -3/2 ) = -3 - 2x[-1.5) = -3 - 2x(-2) = -3 + 4 = 1
所以:
(-2) mod 12 = 12-2=10 (-2) mod 12 = -2 - 12x[-2/12] = -2 - 12x(-1) = -2 + 12 = 10
(-4) mod 12 = 12-4 = 8 (-4) mod 12 = -4 - 12x[-4/12] = -4 -12x(-1) = -4 + 12 = 8
(-5) mod 12 = 12 - 5 = 7 (-5)mod 12 = -5 - 12x[-5/12] = -5 -12x(-1) = -5 + 12 = 7
开始证明
再回到时钟的问题上:回拨2小时 = 前拨10小时,回拨4小时 = 前拨8小时,回拨5小时= 前拨7小时
注意,这里发现的规律!
结合上面学到的同余的概念,实际上:
(-2) mod 12 = 10;10 mod 12 = 10;-2与10是同余的。
(-4) mod 12 = 8;8 mod 12 = 8;-4与8是同余的。
距离成功越来越近了。要实现用正数替代负数,只需要运用同余数的两个定理:
反身性:
a ≡ a (mod m),这个定理是很显而易见的。
线性运算定理:
如果a ≡ b (mod m),c ≡ d (mod m) 那么:
(1)a ± c ≡ b ± d (mod m)
(2)a * c ≡ b * d (mod m)
所以:
7 ≡ 7 (mod 12);(-2) ≡ 10 (mod 12);7 -2 ≡ 7 + 10 (mod 12)
现在我们为一个负数,找到了它的正数同余数。但是并不是7-2 = 7+10,而是 7 -2 ≡ 7 + 10 (mod 12) ,即计算结果的余数相等。
接下来回到二进制的问题上,看一下:2-1=1的问题。
2-1=2+(-1) = [0000 0010]原+ [1000 0001]原= [0000 0010]反+ [1111 1110]反
先到这一步,-1的反码表示是1111 1110。如果这里将[1111 1110]认为是原码,则[1111 1110]原 = -126,这里将符号位除去,即认为是126。
发现有如下规律:(-1) mod 127 = 126;126 mod 127 = 126
即:
2 ≡ 2 (mod 127);(-1) ≡ 126 (mod 127);2-1 ≡ 2+126 (mod 127);2-1 与 2+126的余数结果是相同的!而这个余数,正式我们的期望的计算结果:2-1=1
所以说一个数的反码,实际上是这个数对于一个模的同余数。而这个模并不是我们的二进制,而是所能表示的最大值!这就和钟表一样,转了一圈后总能找到在可表示范围内的一个正确的数值!
而2+126很显然相当于钟表转过了一轮,而因为符号位是参与计算的,正好和溢出的最高位形成正确的运算结果。
既然反码可以将减法变成加法,那么现在计算机使用的补码呢?为什么在反码的基础上加1,还能得到正确的结果?
2-1=2+(-1) = [0000 0010]原+ [1000 0001]原= [0000 0010]补+ [1111 1111]补
如果把[1111 1111]当成原码,去除符号位,则:[0111 1111]原= 127
其实,在反码的基础上+1,只是相当于增加了模的值:
(-1) mod 128 = 127;127 mod 128 = 127;2 ≡ 2 (mod 127);2-1 ≡ 2+127 (mod 128)
此时,表盘相当于每128个刻度转一轮。所以用补码表示的运算结果最小值和最大值应该是[-128, 128]。
-----------------------------------------------------------
---------------------------------------------
朦胧的夜 留笔~~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号