汉诺塔问题

问题：

有64个盘子，大小不等，大的在下，小的在上。把64个盘子由A座移动到C座，每次只能移动一个盘子，移动的过程中保持大盘子在下，小盘子在上。在移动过程中可以利用B座，输出移动步骤。

 

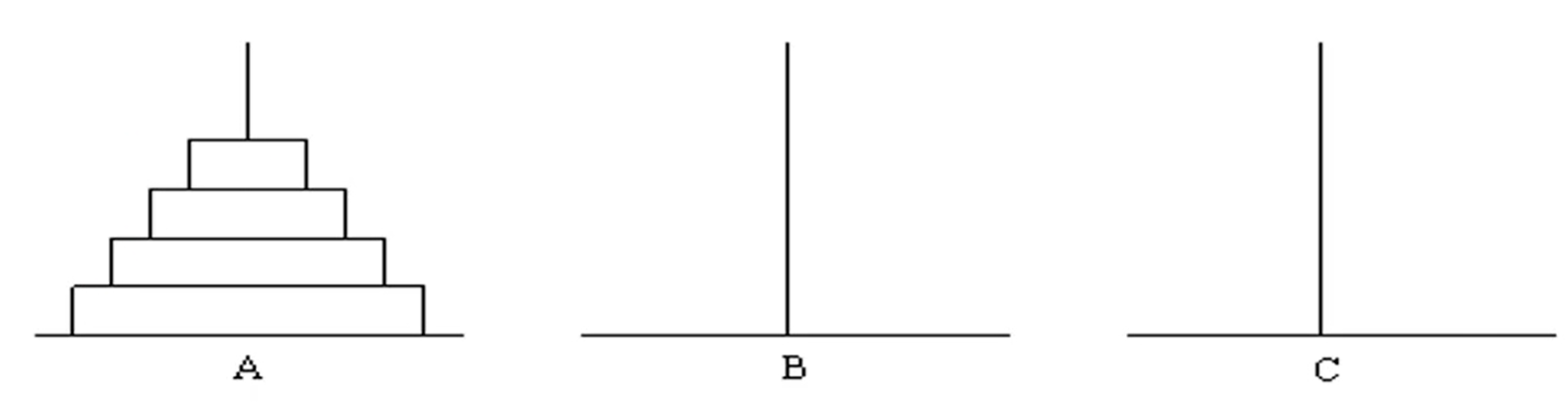
 思路：（将问题转化为形式一样的，更小规模的问题）

1.首先把n-1 个盘子，从A->B,以C为中转

2.把最后一个盘子从 A->C, 以B为中转

3.把n-1个盘子，从B->C，以A为中转

以步骤1中把n-1个盘子，从A->B以C为中转为例，可以分解为：

a.首先把n-2个盘子，从A->C，以B为中转

b.把最大的一个盘子，A->B

c.把n-2个盘子从C->B，以A为中转

以此类推，最终都可以分解到n=1的情况。

 

# hanoi问题
def hanoi(n, src, mid, dest):
    # 将src上的n个盘子，以mid为中转，移动到dest上
    if( n==1 ):
        print(src + '->' + dest)
        return
    hanoi(n-1, src, dest, mid)
    hanoi(1, src, mid, dest)
    hanoi(n-1, mid, src, dest)

n = int(input())
hanoi(n, 'A', 'B', 'C')

 

由以上知:T(n)=2T(n-1)+1,且T(1)=1,可得T(n)=(2^n)-1,所以时间复杂度为 2^n

已知递推公式为：T(n)=2T(n-1)+1，要求通项T(n),可构造构造一个等比数列。

设 T(n)+x=2(T(n-1)+x)， 解得x=1，即有T(n)+1=2(T(n-1)+1)

T(n)+1为等比数列，首项为2，公比为2，所以T(n)+1 = 2*2^(n-1) = 2^n

T(n)=(2^n)-1