二进制、八进制、十进制和十六进制的相互转化（图解）
1. 二进制(B)、八进制(O)和十六进制(H) 转成十进制(D) [1]
-
二进制(B) --> 十进制(D)
方法(B -> D): 二进制数从低位到高位（即从右往左）计算，第0位的权值是2的0次方，第1位的权值是2的1次方，第2位的权值是2的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了;
二进制就是逢2进1，采用 0，1的组合来表达一个数; // 例：将二进制的(101011)B转换为十进制的步骤如下; 第1位 1 x 2^0 = 1; 第2位 1 x 2^1 = 2; 第3位 0 x 2^2 = 0; 第4位 1 x 2^3 = 8; 第5位 0 x 2^4 = 0; 第6位 1 x 2^5 = 32; 读数: 把结果值相加，1+2+0+8+0+32=43，即(101011)B=(43)D -
八进制(O) --> 十进制(D)
方法(O -> D): 八进制数从低位到高位（即从右往左）计算，第0位的权值是8的0次方，第1位的权值是8的1次方，第2位的权值是8的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了;
八进制就是逢8进1，八进制数采用 0～7这八数来表达一个数; // 例：将八进制的(53)O转换为十进制的步骤如下; 第1位 3 x 8^0 = 3; 第2位 5 x 8^1 = 40; 读数: 把结果值相加，3+40=43，即(53)O=(43)D -
十六进制(H) --> 十进制(D)
方法(H -> D): 十六进制数从低位到高位（即从右往左）计算，第0位的权值是16的0次方，第1位的权值是16的1次方，第2位的权值是16的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了;
十六进制就是逢16进1，十六进制的16个数为0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F，其中A~F等值于十进制的10~15; // 例：将十六进制的(2B)H转换为十进制的步骤如下; 第1位 B x 16^0 = 11; 第2位 2 x 16^1 = 32; 读数: 把结果值相加，11+32=43，即(2B)H=(43)D
2. 十进制(D) 转成二进制(B)、八进制(O)和十六进制(H)
-
十进制(D) --> 二进制(B)
方法(D -> B): 除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止;
读数: 从最后一个余数读起，一直到最前面的一个余数;
例：将十进制的(43)D转换为二进制的步骤如下; 1. 将商43除以2，商21余数为1; 2. 将商21除以2，商10余数为1; 3. 将商10除以2，商5余数为0; 4. 将商5除以2，商2余数为1; 5. 将商2除以2，商1余数为0; 6. 将商1除以2，商0余数为1; 读数: 因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，101011，即(43)D=(101011)B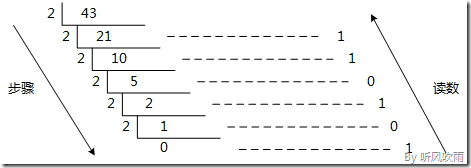
-
十进制(D) --> 八进制(O)
方法1(D -> O): 除8取余法，即每次将整数部分除以8，余数为该位权上的数，而商继续除以8，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止;
读数: 从最后一个余数起，一直到最前面的一个余数;
// 例：将十进制的(796)D转换为八进制的步骤如下; 1. 将商796除以8，商99余数为4; 2. 将商99除以8，商12余数为3; 4. 将商12除以8，商1余数为4; 5. 将商1除以8，商0余数为1; 读数: 因为最后一位是经过多次除以8才得到的，因此它是最高位，读数字从最后的余数向前读，1434，即(796)D=(1434)O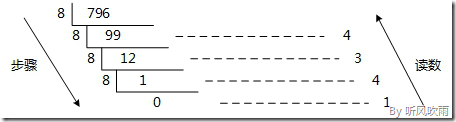
方法2(D -> O): 使用间接法(D -> B -> O)，先将十进制转换成二进制，然后将二进制又转换成八进制;
-
十进制(D) --> 十六进制(H)
方法1(D -> H): 除16取余法，即每次将整数部分除以16，余数为该位权上的数，而商继续除以16，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止;
读数: 从最后一个余数起，一直到最前面的一个余数;
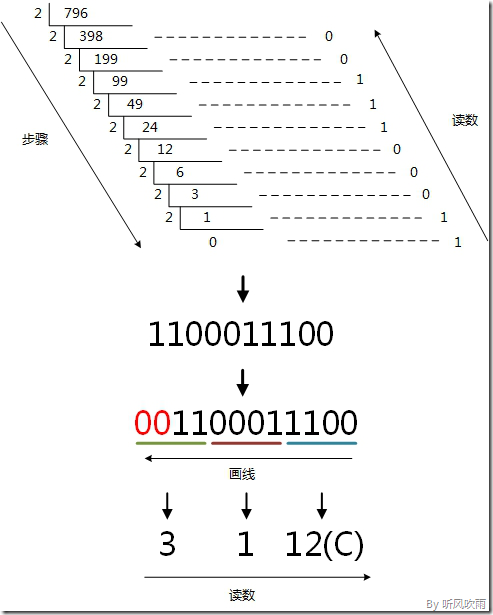
// 例：将十进制的(796)D转换为十六进制的步骤如下; 1. 将商796除以16，商49余数为12，对应十六进制的C; 2. 将商49除以16，商3余数为1; 3. 将商3除以16，商0余数为3; 读数: 因为最后一位是经过多次除以16才得到的，因此它是最高位，读数字从最后的余数向前读，31C，即(796)D=(31C)H
方法2(D -> H): 使用间接法(D -> B -> H)，先将十进制转换成二进制，然后将二进制又转换成十六进制;
3. 二进制(B)、八进制(O)和十六进制(H)互转
-
二进制(B) <--> 八进制(O)
方法(B -> O): 取三合一法，即从二进制的小数点为分界点，向左（向右）每三位取成一位，接着将这三位二进制按权拼接，然后按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数;
如果向左（向右）取三位后，取到最高（最低）位时候，如果无法凑足三位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足三位;
方法(O -> B): 取一分三法，即将一位八进制数分解成三位二进制数，用三位二进制按权相加去凑这位八进制数，小数点位置照旧;
// 例：将二进制的(11010111.0100111)B转换为八进制的步骤如下(从小数点开始往两边画,不足三位补0); 1. 小数点前: 111 = 7; 010 = 2; 11补全为011, 011 = 3; 2. 小数点后: 010 = 2; 011 = 3; 1补全为100，100 = 4; 读数: 读数从高位到低位，即(11010111.0100111)B=(327.234)O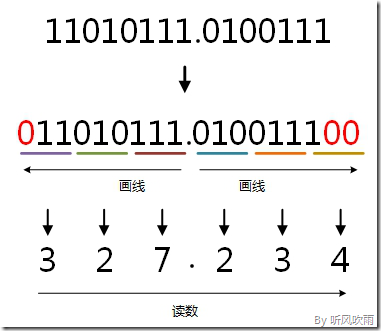
二进制和八进制编码对应表
二进制(B) 八进制(O) 000 0 001 1 010 2 011 3 100 4 101 5 110 6 111 7 -
二进制(B) <--> 十六进制(H)
方法(B -> H): 取四合一法，即从二进制的小数点为分界点，向左（向右）每四位取成一位，接着将这四位二进制按权相拼接，然后按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的十六进制数;
如果向左（向右）取四位后，取到最高（最低）位时候，如果无法凑足四位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足四位;
方法(H -> B): 取一分四法，即将一位十六进制数分解成四位二进制数，用四位二进制按权相加去凑这位十六进制数，小数点位置照旧;
// 例：将二进制的(11010111)B转换为十六进制的步骤如下(从右往左画,不足四位补0)： 0111 = 7; 1101 = D; 读数: 读数从高位到低位，即(11010111)B=(D7)H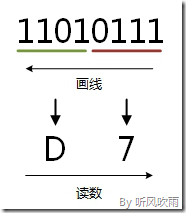
二进制和十六进制编码对应表
二进制(B) 十六进制(O) 0000 0 0001 1 0010 2 0011 3 0100 4 0101 5 0110 6 0111 7 1000 8 1001 9 1010 A 1011 B 1100 C 1101 D 1110 E 1111 F -
八进制(O) <--> 十六进制(H)
方法(O -> H): 使用间接法(O -> B -> H)，先将八进制转换为二进制，然后再将二进制转换为十六进制，小数点位置不变;
方法(H -> O): 使用间接法(H -> B -> O)，先将十六进制转换为二进制，然后再将二进制转换为八进制，小数点位置不变;
// 例：将八进制的(327)O转换为十六进制的步骤如下： 1. 八进制(327)O转换成二进制; 3 = 011; 2 = 010; 7 = 111; 2. 得到(011010111)B, 再转换成十六进制; 0111 = 7; 1101 = D; 读数: 读数从高位到低位，D7，即(327)O=(D7)H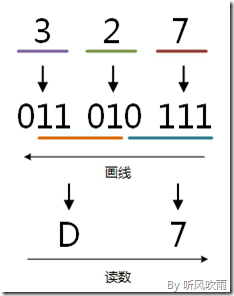
4. 扩展阅读
-
幂计算
// 1. 包含小数的进制换算： (ABC.8C)H = 10x16^2 + 11x16^1 + 12x16^0 + 8x16^-1 + 12x16^-2 = 10x16^2 + 11x16^1 + 12x16^0 + 8x(1/16^1) + 12x(1/16^2) = 2560 + 176 + 12 + 0.5 + 0.046875 = (2748.546875)D // 2. 负次幂的计算： 2^-5 = 2^(0-5) = 2^0 / 2^5 = 1 / 2^5
在数字后面加上不同的字母来表示不同的进位制。B（Binary)表示二进制，O（Octal）表示八进制，D（Decimal）或不加表示十进制，H（Hexadecimal）表示十六进制。例如：(101011)B = (53)O = (43)D = (2B)H ↩︎
