【上三角下三角对称矩阵】
/*
上三角下三角对称矩阵
说明: 上三角矩阵是矩阵在对角线以下的元素均为0,即A ij = 0,i > j,例如: 1 2 3 4 5 0 6 7 8 9 0 0 10 11 12 0 0 0 13 14 0 0 0 0 15 下三角矩阵是矩阵在对角线以上的元素均为0,即A ij = 0,i < j,例如: 1 0 0 0 0 2 6 0 0 0 3 7 10 0 0 4 8 11 13 0 5 9 12 14 15 对称矩阵是矩阵元素对称于对角线,例如: 1 2 3 4 5 2 6 8 8 9 3 7 10 11 12 4 8 11 13 14 5 9 12 14 15 上三角或下三角矩阵也有大部份的元素不储存值(为0),我们可以将它们使用一维阵列来储存以节省储存空间,而对称矩阵因为对 称于对角线,所以可以视为上三角或下三角矩阵来储存。 解法: 假设矩阵为nxn,为了计算方便,我们让阵列索引由1开始,上三角矩阵化为一维阵列,若以列为主,其公式为: loc = n*(i-1) - i*(i-1)/2 + j化为以行为主,其公式为:loc = j*(j-1)/2 + i 下三角矩阵化为一维阵列,若以列为主,其公式为:loc = i*(i-1)/2 + j 若以行为主,其公式为:loc = n*(j-1) - j*(j-1)/2 + i 公式的导证其实是由等差级数公式得到,您可以自行绘图并看看就可以导证出来,对于C/C++或Java等索引由0开始的语言来说,只要 将i与j各加1,求得loc之后减1即可套用以上的公式 */ #include<stdio.h> #include<stdlib.h> #define N 5 int main(void){ int arr1[N][N] = { {1,2,3,4,5}, {0,6,7,8,9}, {0,0,10,11,12}, {0,0,0,13,14}, {0,0,0,0,15} }; int arr2[N*(1+N)/2] = {0}; int i, j, loc = 0; printf("原二维矩阵: \n"); for(i = 0; i < N; i++){ for(j = 0; j < N; j++){ printf("%4d", arr1[i][j]); } printf("\n"); } printf("\n以列为主: "); for(i = 0; i < N; i++){ for(j = 0; j < N; j++){ if(arr1[i][j] != 0){ arr2[loc++] = arr1[i][j]; } } } for(i = 0; i < N*(1+N)/2; i++){ printf("%d ", arr2[i]); } printf("\n输入索引(i, j): "); scanf("%d %d", &i, &j); loc = N * i - i * (i + 1) / 2 + j; printf("(%d, %d) = %d", i, j, arr2[loc]); printf("\n"); return 0; }
运行结果:
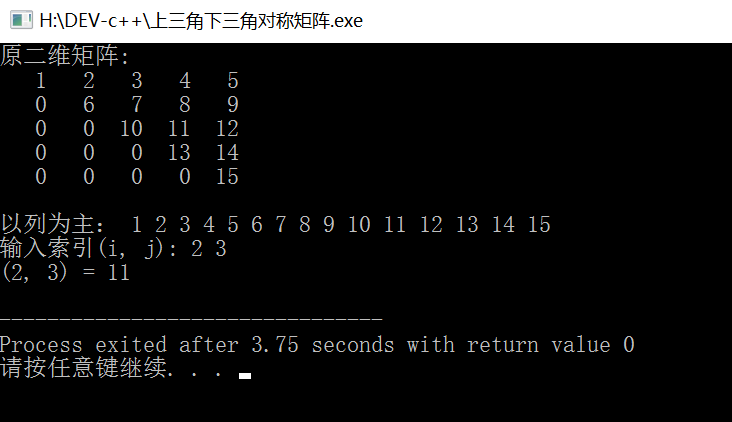
转载本博请联系作者! 如有问题请在评论区评论或者发邮件:@libras


