作者推荐 | 【分布式技术专题】「架构设计方案」图解学习法总结集群模式下的各种软负载均衡策略实现及原理分析

背景介绍

在分布式系统中，负载均衡是非常重要的环节，通过负载均衡将请求派发到网络中的一个或多个节点上进行处理。

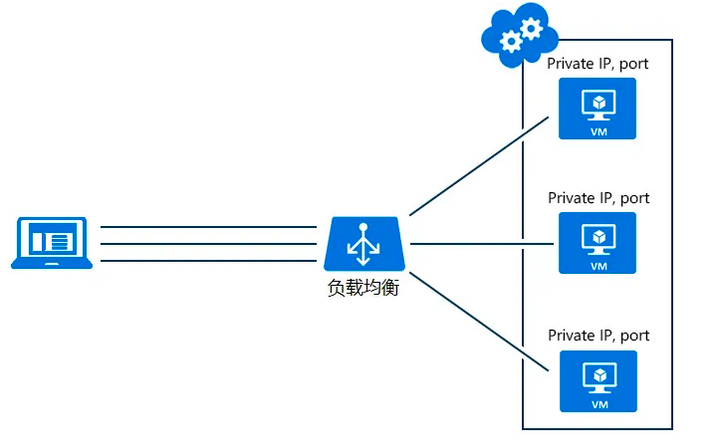
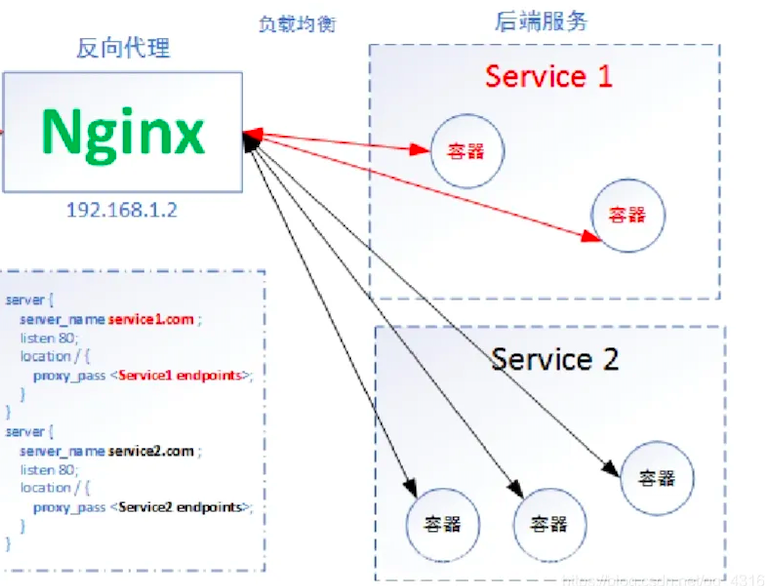
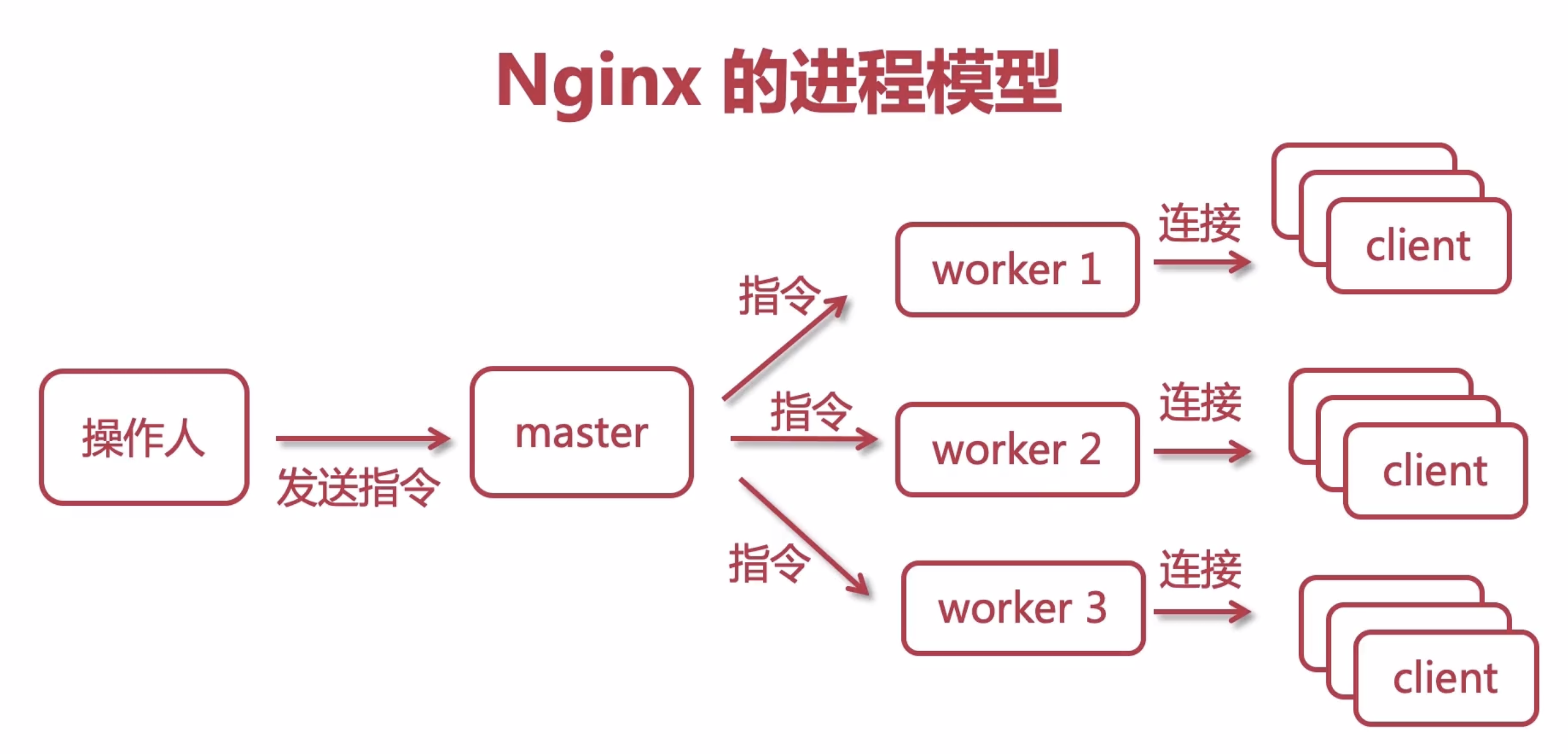
通常来说，负载均衡分为硬件负载均衡及软件负载均衡。硬件负载均衡，顾名思义，在服务器节点之间安装专门的硬件进行负载均衡的工作，F5或者A10便为其中的佼佼者。软件负载均衡则是通过在服务器上安装的特定的负载均衡软件或是自带负载均衡模块完成对请求的分配派发。例如，平时我们使用的Nginx或者API-Gateway网关服务就主要采用负载均衡的方式去转发分派下游服务。

负载均衡的算法策略

一般而言，有以下几种常见的负载均衡策略：

轮询机制（一般默认的策略）

【轮询机制】作为非常经典的负载均衡策略，早期该策略应用地非常广泛。

算法原理

其原理很简单，给每个请求标记一个序号，然后将请求依次派发到服务器节点中，适用于集群中各个节点提供服务能力等同且无状态的场景。算法实现原理图如下所示。

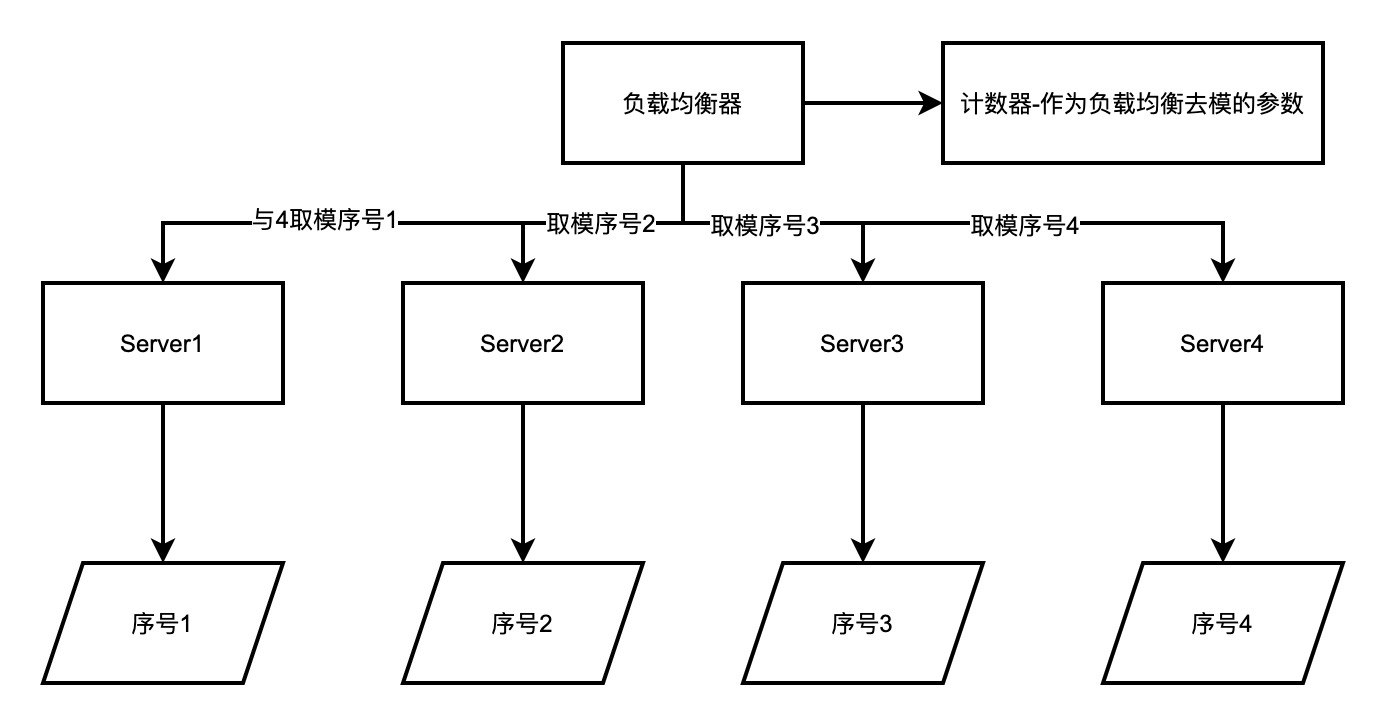
该算法原理三要素

• 为每个服务器进行建立一个编号或者序号（作为唯一标识）。

• 负载均衡器这一侧需要建立一个全局的计数器，作为负载均衡的参数。每次调用都进行+1

• 当负载均衡器的计数器当前值与下游服务的数量取模之后，会得出对应的序号值，则回去进行分派到对应序号值的下游服务即可。

缺略优点

实现比较简单，均衡化较好，每一个节点都属于公平化分配，（上面也说到了）比较适合相同场景和条件规则下的所有下游服务。

策略缺点

缺点也非常明显，该策略将节点视为等同，与实际中复杂的环境不符。加权轮询为轮询的一个改进策略，每个节点会有权重属性，但是因为权重的设置难以做到随实际情况变化，仍有一定的不足。

---

随机机制

【随机机制】与轮询相似，只是不需要对每个请求进行编号，每次随机取一个下游服务节点即可。

算法原理

其原理也很简单，就是采用随机算法或者散列算法将请求服务进行随机散列到下游的不同的服务节点，该策略也将后端的每个节点是为等同的。

另外同样也有改进的加权随机的算法，不再赘述，然后将请求依次派发到服务器节点中，适用于集群中各个节点提供服务能力等同且无状态的场景。算法实现原理图如下所示。

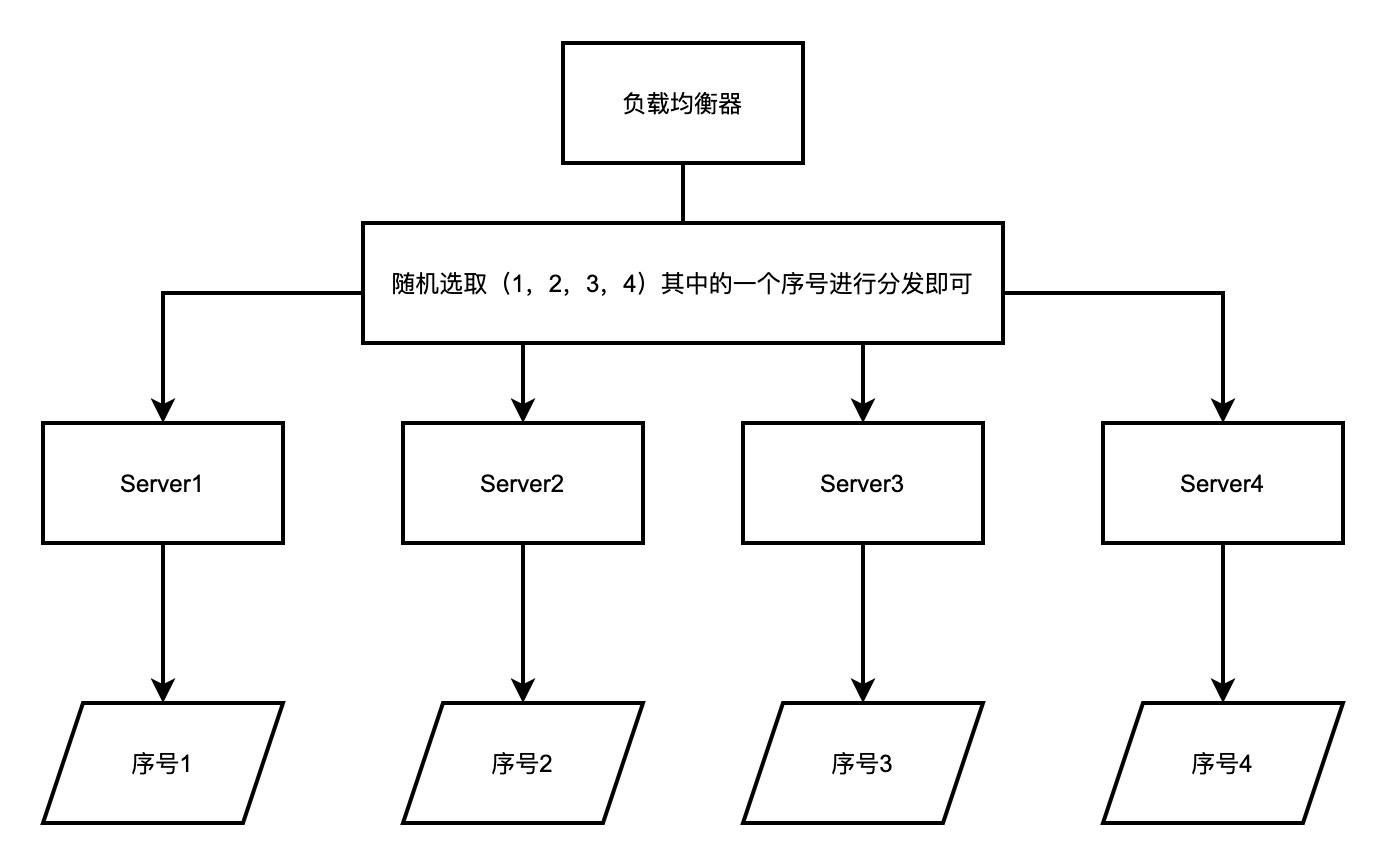
主要依靠于随机算法或者随机组件去生产随机值之后在进行取模就可以。

该算法原理三要素

• 为每个服务器进行建立一个编号或者序号（作为唯一标识）。

• 负载均衡器这一侧需要建立一个随机数算法组件。每次调用都进行分配。

• 然后选取随机值对应的服务组件即可（可以取模、也可以采用随机数从该范围内选取的方式）

缺略优点

实现比较简单，随机性较好，每一个节点都属于公平化分配，（上面也说到了）比较适合相同场景和条件规则下的所有下游服务。

策略缺点

缺点也非常明显，该策略将节点视为等同，与实际中复杂的环境不符。加权轮询为轮询的一个改进策略，每个节点会有权重属性，但是因为权重的设置难以做到随实际情况变化，仍有一定的不足。

---

最小响应时间

通过记录每次请求所需的时间，得出平均的响应时间，然后根据响应时间选择最小的响应时间。

算法原理

该策略能较好地反应服务器的状态，但是由于是平均响应时间的关系，时间上有些滞后，无法满足快速响应的要求。因此在此基础之上，会有一些改进版本的策略，如只计算最近若干次的平均时间的策略等。算法需要进行有状态话的方式进行统计每一次请求，算法实现原理图如下所示。

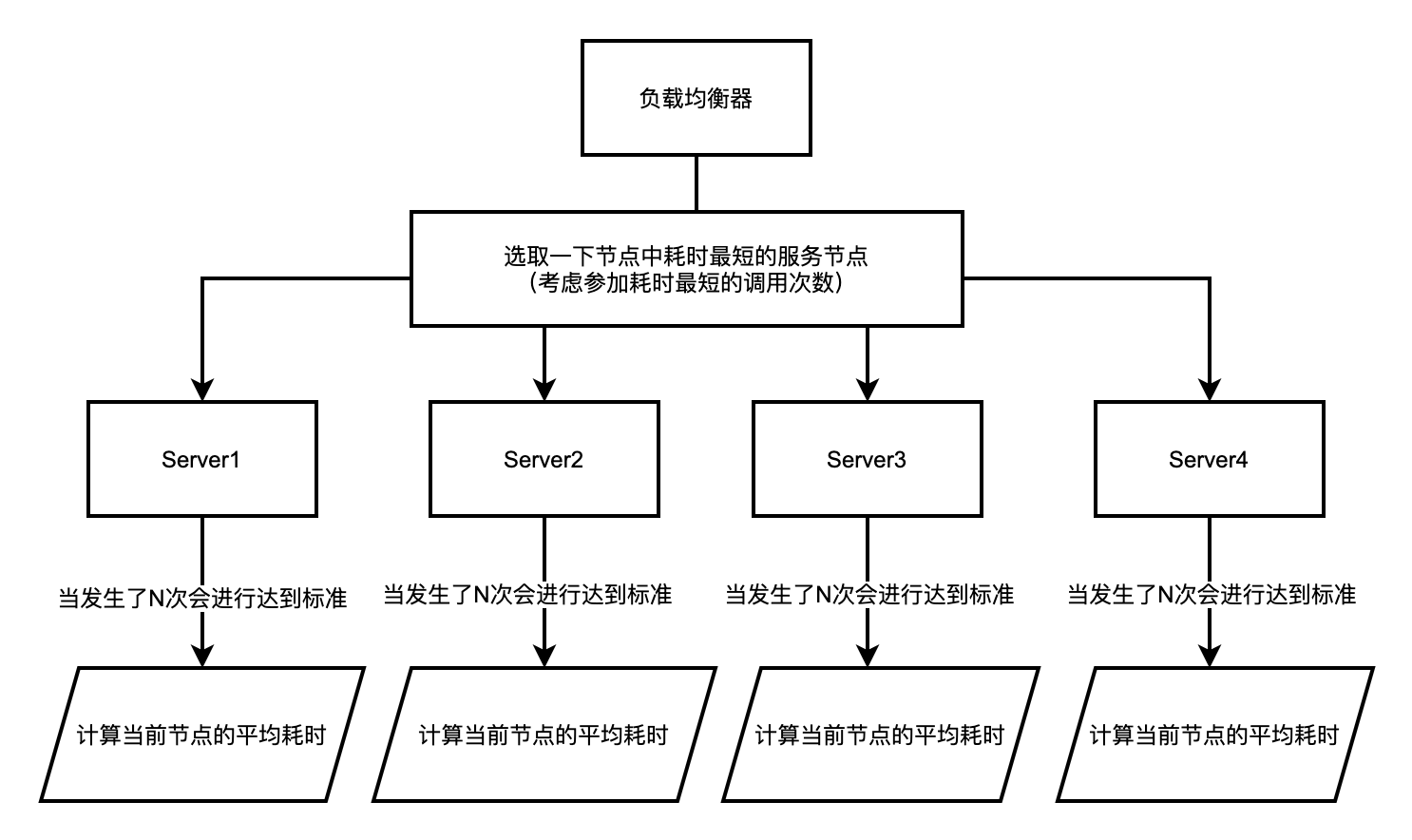
主要依靠于随机算法或者随机组件去生产随机值之后在进行取模就可以。

该算法原理三要素

• 不需要为每一个服务节点建立序号了，但是需要进行对每一个服务节点采用一个bucket存储对应的调用次数以及调用的耗时总和。作为计算平均耗时的依据。

• 耗时选择器：在负载均衡器端调用的时候，将建立一个顺序性队列，存放依据最短耗时（正序）排序的方式存储的队列模型，故此每次可以取队首位置的元素节点作为最短耗时服务节点。

  • 当然，也可以将每次最短的耗时时间的服务节点直接存储在负载均衡器节点中，这样会提高相应的性能，

• 然后选取随机值对应的服务组件即可（可以取模、也可以采用随机数从该范围内选取的方式）

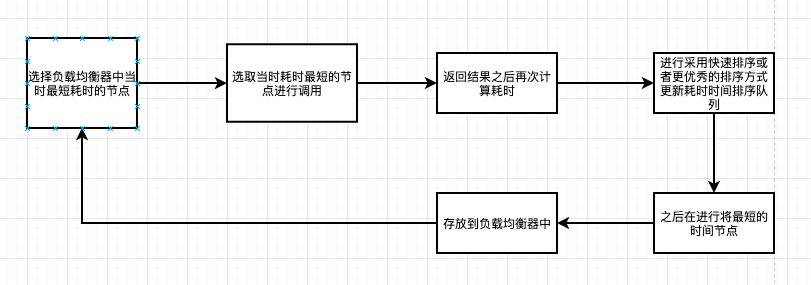
缺略优点

• 可以依据实际情况进行动态计算最合适的服务节点进行调用，可以实现能者多劳，让优秀的服务节点更加出色的发挥其作用，慢慢的可以屏蔽掉不好用或者有问题的节点。

• 可以促使性能和服务能力、可以体验度达到一个比较高的高度和效果。

策略缺点

• 性能会造成一段时间的影响，如果不考虑绝对一致性，也可以后台进行异步计算进行可以能减低每次计算排序服务节点所造成的耗时。

• 此外还可以考虑当不存在最短耗时记录的时候其算法是存在短时间不可靠的问题，随意最好可以做一下提前预热模式。

• 客观问题是否如何排除，当由于网络因素导致某几次该节点的耗时耗费很久，会导致算法模式的影响，所以是否以及选取合适的调用次数统计阈值是一个需要好好考虑的问题。例如只有当调用5次以上才进行计算平均耗时，否则不会考虑其计算，好比一个服务节点只调用了一次并且耗时非常少，其实这个节点耗时计算过于主观以及巧合。

---

最小并发数

客户端的每一次请求服务在服务器停留的时间可能会有较大的差异，随着工作时间加长,如果采用简单的轮循或随机均衡算法,每一台服务器上的连接进程可能会产生较大的不同,并没有达到真正的负载均衡｡

算法原理

最小并发数的策略则是记录了当前时刻，每个备选节点正在处理的事务数，然后选择并发数最小的节点。该策略能够快速地反应服务器的当前状况，较为合理地将负责分配均匀，适用于对当前系统负载较为敏感的场景。

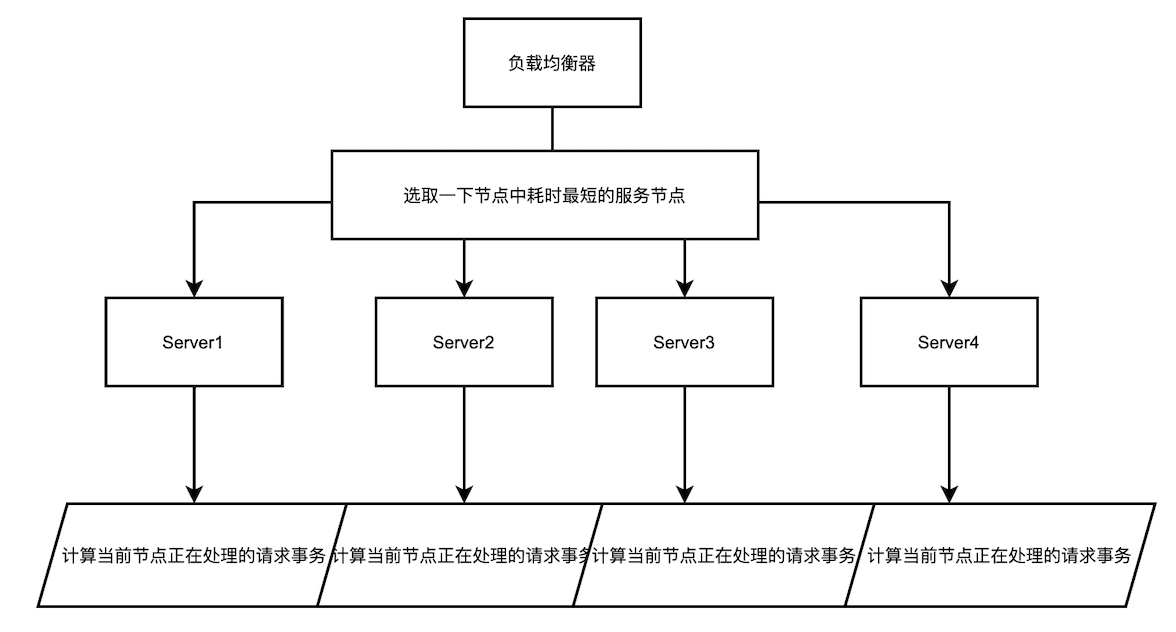
该算法原理三要素

• 当处理请求接收的时候为该节点的计数器+1

• 当返回并且释放请求的时候为该节点的计数器-1

• 每次依据每个后台异步计算的排序队列进行选取最短的节点作为每次请求的首选服务节点。（排序规则为：从小打到去进行依据当前处理事务数进行排序），

缺略优点

• 可以依据实际情况进行动态计算最合适的服务节点进行调用，可以让大家动态化实现的均衡模式进行分配，让每一个节点都可以充分进行处理请求，而不是压在某一个或者某几个服务节点进行处理，其他节点变得过于空闲。适用于集群中各个节点提供服务能力等同且无状态的场景，比起轮询模式其动态化更好。

• 可以促使性能和服务能力、可以体验度达到一个比较高的高度和效果。

策略缺点

• 与最小耗时相同，性能会造成一段时间的影响，如果不考虑绝对一致性，也可以后台进行异步计算进行可以能减低每次计算排序服务节点所造成的耗时。

---

哈希散列

在后端节点有状态的情况下，需要使用哈希的方法进行负载均衡，此种情况下情况比较复杂。可以理解为轮询模式的升级版，在这里不是单纯的考虑取模的计算方式，而是采用key的方式进行计算-依赖于hash函数进行计算。

算法三要素

• hash值映射表，用于计算提供路由能力，方便负载均衡器选取计算后的Hash值与节点的Hash标准值进行匹配路由。

• hash值计算器：主要用于计算每一个服务节点的hash计算值，以及每次请求的hash值，从而进行数据对比。

算法优点

• 散列性和公平性更加的优秀和完善
• 性能计算非常的不错，接近于O(1)的时间复杂度。
• 与轮询一样，思路较为简单。
• 可以实现相同的条件，会实现数据指纹模式，数据请求追踪方式，例如：原始ip - 会匹配相同的服务节点，达成请求的有状态话。目前nginx常会使用 ip-hash算法、url-hash算法模式。

算法缺点

• 强依赖于Hash算法和Hash组件
• 对于时间复杂度而言降低很多，但是其依靠的是增加了空间复杂度。

---

分布式系统容错性因素分析

分布式系统面临着远比单机系统更加复杂的环境，包括不同的网络环境、运行平台、机器配置等等。在如此复杂的环境中，发生错误是不可避免的，然后如何能够做到容错性，将发生错误的代价降低到最低是在分布式系统中必须要考虑的问题。

分布式系统算法的实际选择

前提背景

选择不同的负载均衡策略将会有非常大的不同，考虑下列的情况。完成请求需要如下四个集群，A,B,C,D，其中，假定完成调用需要调用集群B3次，B集群共有5台服务器。

单次调用概率计算

当集群B中的某台服务器出现故障而导致无法提供服务，若集群中其他容错手段尚未生效，那么理想情况下，4/5的请求不受影响。

采用轮询或随机的负载均衡策略

单次请求派发到正常节点的概率为4/5，那么该请求成功的机率为 (4/5) * (4/5) * (4/5) = 64/125 ：约为二之一，低于4/5的理想状态。

在因此，在此种情况下，若仅仅采用此种策略，会使故障的影响范围扩散，不符合预期。

采用最小并发数的复杂均衡策略

假定正常一个请求需耗时10ms，超时时间设置为1s，那么，按照最小并发数的策略，异常节点的提供服务的能力为1，正常节点提供服务能力为100，则派发到异常节点的概率为1/(100 * 4+1)=1/401，该请求成功的几率为1(400/401)^3≈99.25%，高于4/5。

计算的公式

更加一般地，设集群中发生故障的故障机器的比例p，那么调用失败的预期概率为

1/(100 * 4+1)=1/401
p * 1/401 = N

N为最后的预测调用失败的概率，对应的成功的概率就为：

(1-p) * 1/401 = M 或 1 - N 

计算的公式

整个请求需要调用k次，若采用轮询或随机的负载均衡策略，那么单次派发到正常节点的概率为多少？有上面的计算分析的思路可以了解到：（1-P）为正常机器的比例，那么K次就是：（1-P）的K次方。请求的成功率便会下降低于单次的（1-P）。

当k为3的时候，得到成功率f(p)与p的关系：

f(p) = (1-p) ^n

从上面的公式可知，在p在增大的时候，请求的成功率f(p)便会有明显的下降，故而在对可靠性要求比较高的分布式系统中，不能简单地采用此种策略。

采用最小并发数的策略

假设集群服务器的总数为m，假定异常情况下服务能力下降到正常的1/q，那么单位时间内，集群能提供服务的总数为：m * (1- 1/q) ，那么单次派发到正常节点的概率为:

m * (1- 1/q) / m

请求的成功率则是上述值的k次方，即

m * (1- 1/q) / m ^k

1. 当p在较小的区间内变化时(如(0,0.4])，随着p的增大,成功率f(p)并未有明显的下降，在每个节点可以承受服务压力的情况下，可以良好地处理多个节点故障的异常状况。

2. 换个角度思考，再挖掘一下上述等式，若p为恒定，即集群中若已有一定数量的机器发生了故障。

3. 所以服务的超时时间无须设置地过大，一般来说，设置为10倍的正常提供服务器时间即可。

在此种情况下，会导致失败大大提升，即使只有较小比例的集群出现异常，也会使得请求大量失败，故而还需要其他手段检测到此类型的异常。

最后的总结

在实际应用中，客户端的并发数可能存在一直维持在一个较低的水平上，由于客户端的并发数并不能代表服务端的并发情况，会造成在客户端并发数较小的情况下，服务端实际负载不均衡的状况。

故而，最小并发数的负载均衡策略不适用于在客户端做负载均衡，且客户端负载较小的情况。这种情况下，目前采用随机的方法解决负载不均衡的问题。当然，在实际的分布式系统中，因为一个节点异常而导致其他节点的压力增大，可能会使其他节点的性能下降，他们之间的关系难以用上述的等式简单地描述。