day44 377. 组合总和 Ⅳ |

给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。

示例:

nums = [1, 2, 3]
target = 4

所有可能的组合为： (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)

请注意，顺序不同的序列被视作不同的组合。

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (i >= nums[j]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:

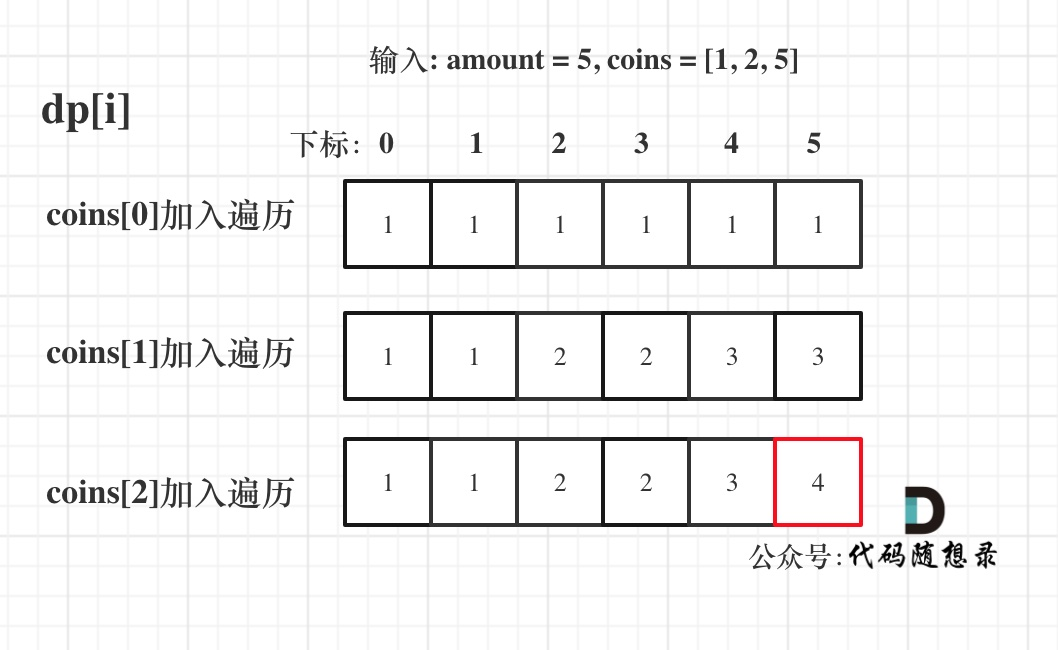
输入: amount = 5, coins = [1, 2, 5]
输出: 4

解释: 有四种方式可以凑成总金额:

5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount + 1];
        //初始化dp数组，表示金额为0时只有一种情况，也就是什么都不装
        dp[0] = 1;
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}